
(i) Find the equivalent capacitance of the combination shown in the figure (a), when C1=2.0μF,C2=4.0μFandC3=3.0μF
(ii) The input terminals A and B in Fig. (a) are connected to a battery of 12 V. Find the potential and the charge of each capacitor.
(a) C1and C2 are in parallel hence their equivalent capacitance is
C'=C1+C2=2.0μF+4.0μF=6.0μF
Figure (b) shows the combination of C' and C3 in series. The final equivalent capacitance shown in figure ( c) is given by
1Cεq=1C'+1C3=16.0μF+13.0μF=12.0μF
or Ceq=2.0μF
(b) To find the charge or potential difference , we retrace the path to the original in figure (a) The charge supplied by the battery is
q=CeqV when the inputs are joined to a V-volt battery
=(2.0μF)(12.0V)=24.0μC
The charge on each capacitor in series in figure (b ) is
q3=q=q=24.0μC
So V3=q3C3=24.0μC3.0μF8V
The potential difference across C in figure ( b) is
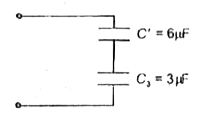
V=qC=24.0μC6.0μF=4V (b) C1andC2 in figure (a) and hence the charges on them are
q1=C1V1=(2.0μF)(4.0V)=8.0μC
and q2=C2V2=(4.0μF)(4.0V)=16.μC
Thus we have V1=V2=4.0V,V3=8V

and q1=8.0μC,q2=16.0μC,q3=24.0μC (c) C' and C3 are replaced by Ceq
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXERCISE
20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - A
44 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-J Aakash Challengers Questions
5 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
Find the charges on the three capacitors connected to a bettery as shown in figure (31.E1). Take C_1=2.0,muF, C_2=4.0,muf, C_3=6.0,muF and V=12 volts.

View SolutionThe equivalent capacity between A and B in the given circuit is (C1=4μF,C2=12μF,C3=8μF,C4=4μF,C5=8μF)

View Solution(i) Find equivalent capacitance between A and B in the combination give below . Each capacitor is a of 2μF capacitance .

View SolutionIn the given network capacitance, C1=10μF,C2=5μF and C3=4μF. What is the resultant capacitance between A and B?
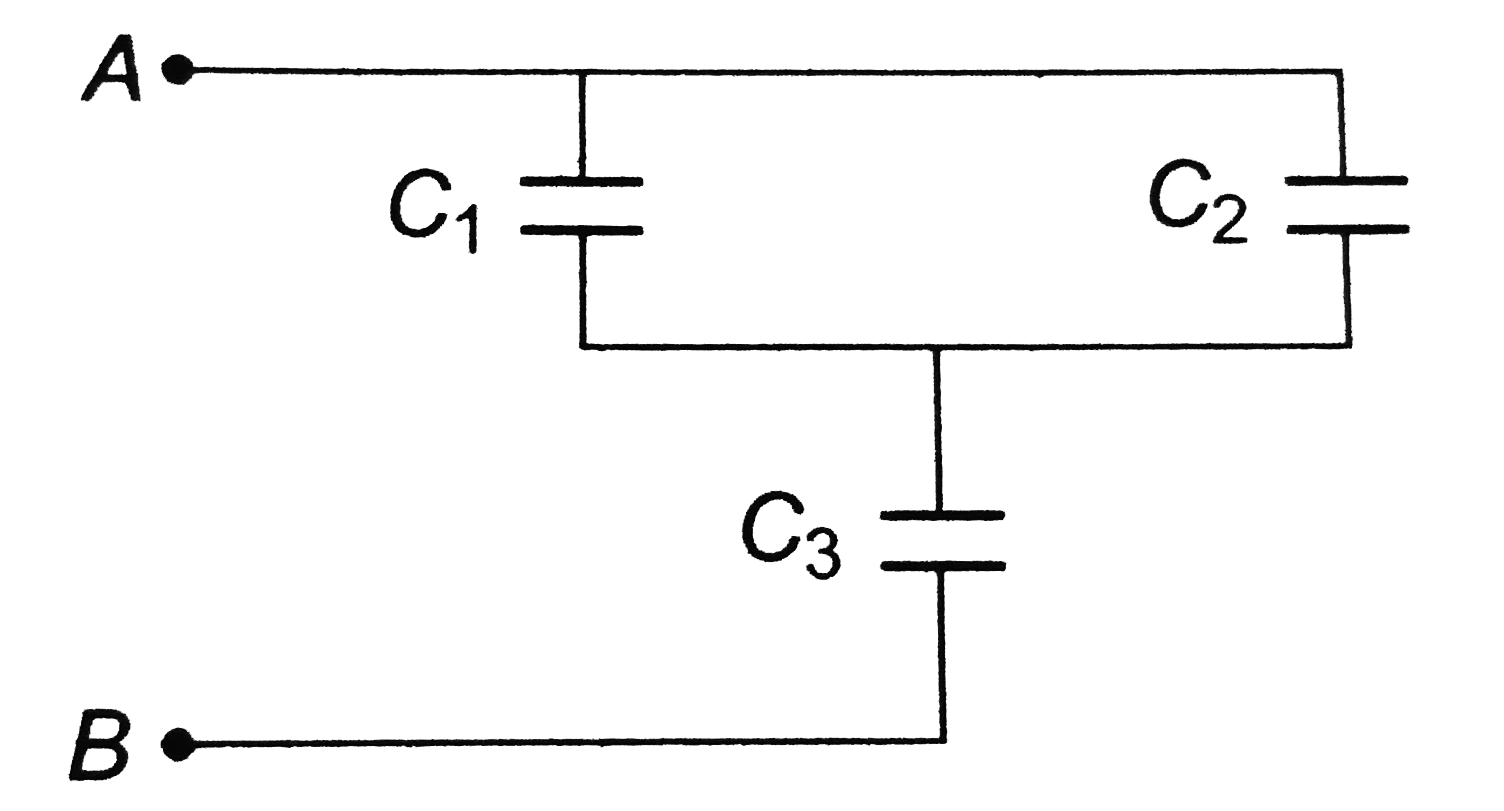
View SolutionIn the given network capacitance, C1=10μF,C2=5μF and C3=4μF. What is the resultant capacitance between A and B?

View SolutionThree capacitors C1=6μF,C2=12μF and C3=20μF are connected to a 100 V battery, as shown in figure below:
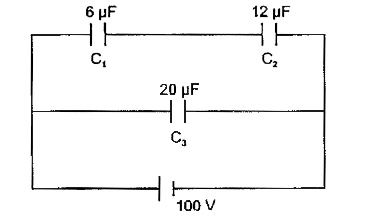
(i) Charge on each plate of capacitor C1.
(ii) Electrostatic potential energy stored in capacitor C3.
View SolutionA potential of V=3000V is applied to a combination of four initially uncharged capacitors as shown in the figure. Capacitors A, B, C and D have capacitances CA=6.0μF,CB=5.2μF,CC=1.5μFandCD=3.8μF, respectiely. If the battery is disconnected, then potential difference across capacitor B is (approximately)

View SolutionIf the equivalent capacitance between points P and Q of the combination of the capacitors show in figure below us 30μF, the capacitor C is

View Solution(a) Find the equivalent capacitance of the combination between A and B in the figure
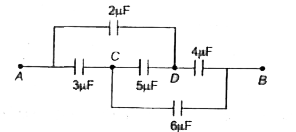
If the points A and B are maintained at 15 V and 0 V respectively then
(b) Find the charges on 3μF,4μFand 5μF capacitors
(c ) What are the potentials of the points C and D ?
View SolutionIn, given C1=3μF,C2=5μF,C3=9μF, and C4=13μF. What is the potential differnce between points A and B?
 .
.
View Solution
