Three capcaitors of capacities 1μF,2μF and 3μF are charged by 10V,20V and 30V respectively. Now positive plates of first two capacitors are connected with the negative plate of third capacitor on one side and negative plates of first wo capacitors are connectes with positive of third capacitor on the other side. Find
a. common potential V
b. final charges on different capacitors.
To solve the problem step by step, we will follow the outlined procedure to find the common potential V and the final charges on the different capacitors.
Step 1: Calculate the initial charges on each capacitor
The charge Q on a capacitor can be calculated using the formula:
Q=C×V
where C is the capacitance and V is the voltage.
1. For the first capacitor (1 µF charged at 10 V):
Q1=1μF×10V=10μC
2. For the second capacitor (2 µF charged at 20 V):
Q2=2μF×20V=40μC
3. For the third capacitor (3 µF charged at 30 V):
Q3=3μF×30V=90μC
Step 2: Determine the total charge in the system
When the capacitors are connected as described, we need to consider the polarity of the charges. The positive plates of the first two capacitors are connected to the negative plate of the third capacitor, and the negative plates of the first two capacitors are connected to the positive plate of the third capacitor.
The total charge Q in the system can be calculated as:
Q=Q3−Q1−Q2
Substituting the values:
Q=90μC−10μC−40μC=40μC
Step 3: Calculate the total capacitance of the system
The total capacitance C of the system can be calculated by summing the capacitances of the three capacitors:
C=C1+C2+C3=1μF+2μF+3μF=6μF
Step 4: Calculate the common potential V
The common potential V across the system can be calculated using the formula:
V=QC
Substituting the values:
V=40μC6μF=406=203V
Step 5: Calculate the final charges on each capacitor
Now we can find the final charges on each capacitor using the common potential V:
1. Final charge on the first capacitor Q′1:
Q′1=V×C1=203V×1μF=203μC
2. Final charge on the second capacitor Q′2:
Q′2=V×C2=203V×2μF=403μC
3. Final charge on the third capacitor Q′3:
Q′3=V×C3=203V×3μF=20μC
Summary of Results
- Common potential V=203V
- Final charges:
- Q′1=203μC
- Q′2=403μC
- Q′3=20μC
The charge Q on a capacitor can be calculated using the formula:
Q=C×V
where C is the capacitance and V is the voltage.
Q1=1μF×10V=10μC
Q2=2μF×20V=40μC
Q3=3μF×30V=90μC
When the capacitors are connected as described, we need to consider the polarity of the charges. The positive plates of the first two capacitors are connected to the negative plate of the third capacitor, and the negative plates of the first two capacitors are connected to the positive plate of the third capacitor.
Q=Q3−Q1−Q2
Substituting the values:
Q=90μC−10μC−40μC=40μC
The total capacitance C of the system can be calculated by summing the capacitances of the three capacitors:
C=C1+C2+C3=1μF+2μF+3μF=6μF
The common potential V across the system can be calculated using the formula:
V=QC
Substituting the values:
V=40μC6μF=406=203V
Now we can find the final charges on each capacitor using the common potential V:
Q′1=V×C1=203V×1μF=203μC
Q′2=V×C2=203V×2μF=403μC
Q′3=V×C3=203V×3μF=20μC
- Common potential V=203V
- Final charges:
- Q′1=203μC
- Q′2=403μC
- Q′3=20μC
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - Exercise
155 Videos
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
Two capacitors of 2μF and 3μF are charged to 150V and 120V, respectively. The plates of capacitor are connected as shown in the figure. An uncharged capacitor of capacity 1.5μF falls to the free end of the wire. Then
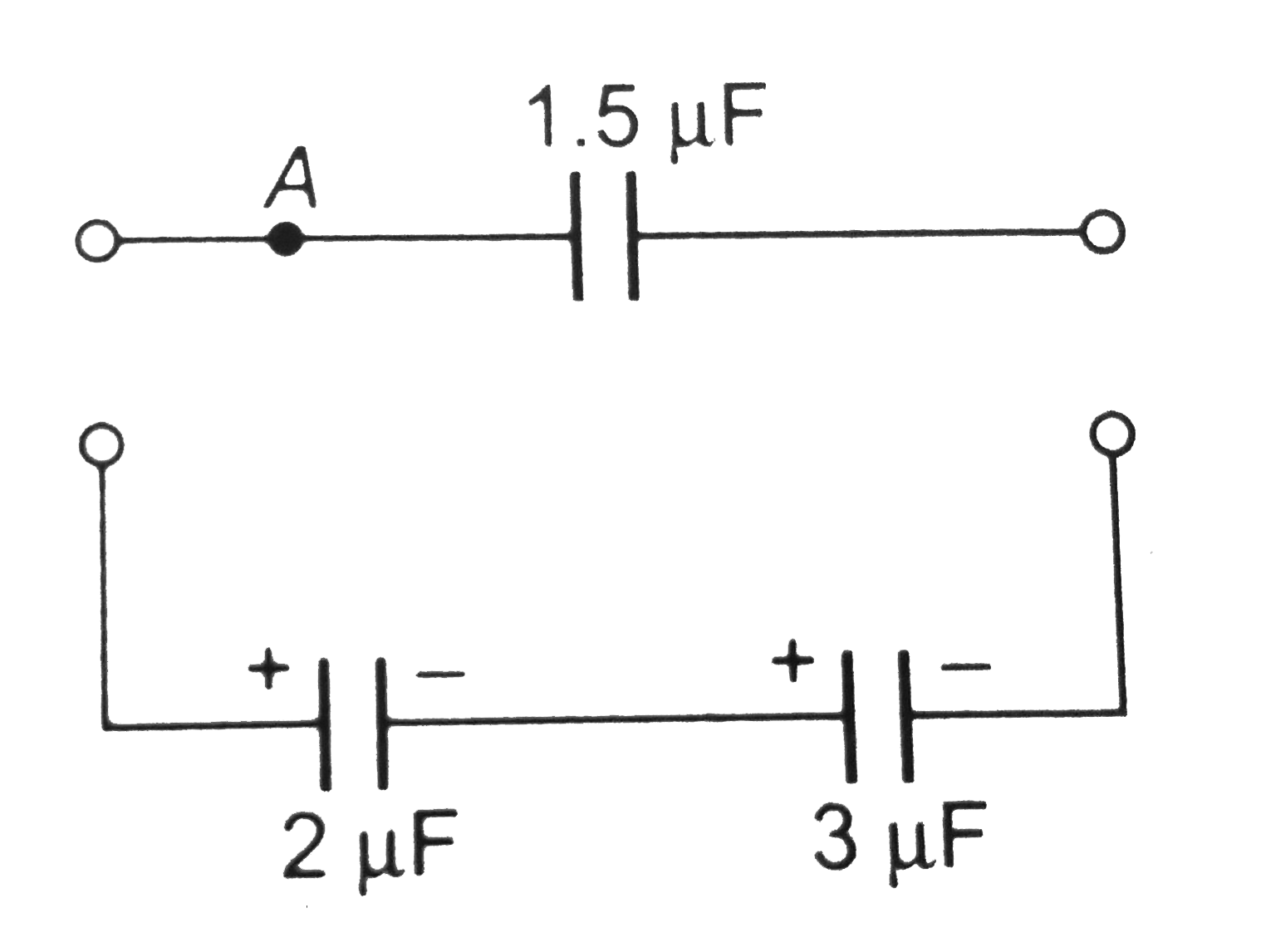
View SolutionTwo capacitors of 2μF and 3μF are charged to 150V and 120V, respectively. The plates of capacitor are connected as shown in the figure. An uncharged capacitor of capacity 1.5μF falls to the free end of the wire. Then

View SolutionTwo capacitors of capacitance 2μFand5μF are charged to a potential difference 100V and 50 V respectively and connected such that the positive plate of one capacitor is connected to the negative plate of the other capacitor after the switch is closed, the initial current in the circuit is 50 mA. the total resistance of the connecting wires is (in Ohm):
View SolutionTwo capacitors of capacitance 2μF and 3μF respectively are charged to potential difference 20 V and 40 V respectively. Now the capacitors are connected in series with a resistance such that the positively charged plate of one capacitor is connected to the positively charged plate of the other. The initial current through the resistance is I0. The potential difference across the 2μF capacitor at the instant the current has reduced to I02 is_______ V.
View Solution
Three capacitors of capacitances 5μF,2μF and 2μF are charged to 20 V, 30 V and 10 V respectively and then connected in the circuit with polarities as shown. The magnitude of charge flown through the battery after closing the switch S is
View SolutionTwo parallel plates capacitors A and B having capacitance of 1μFand5μF are charged separately to the same potential of 100 V. Now, the positive plate of A is connected to the negative plate of B and the negative plate of A to the positive plate of B. Find the final charges on each capacitors.
View SolutionTwo capacitors A and B with capacities 3μF and 2μF are charged to a potential differece of 100V and 180V, respectively. The plates ot the capacitors are connected as shown in, with one wire free from each capacitor. The upper plate of A is positive and that of B is negative An uncharged 2μF capacitor C with lead wires falls on the free ends to complete the circuit.
i. Calculate the final charge on the three capacitors,
ii. Find the amount of electrostatic energy stored in the system before and after the completion of the circuit.
 .
.
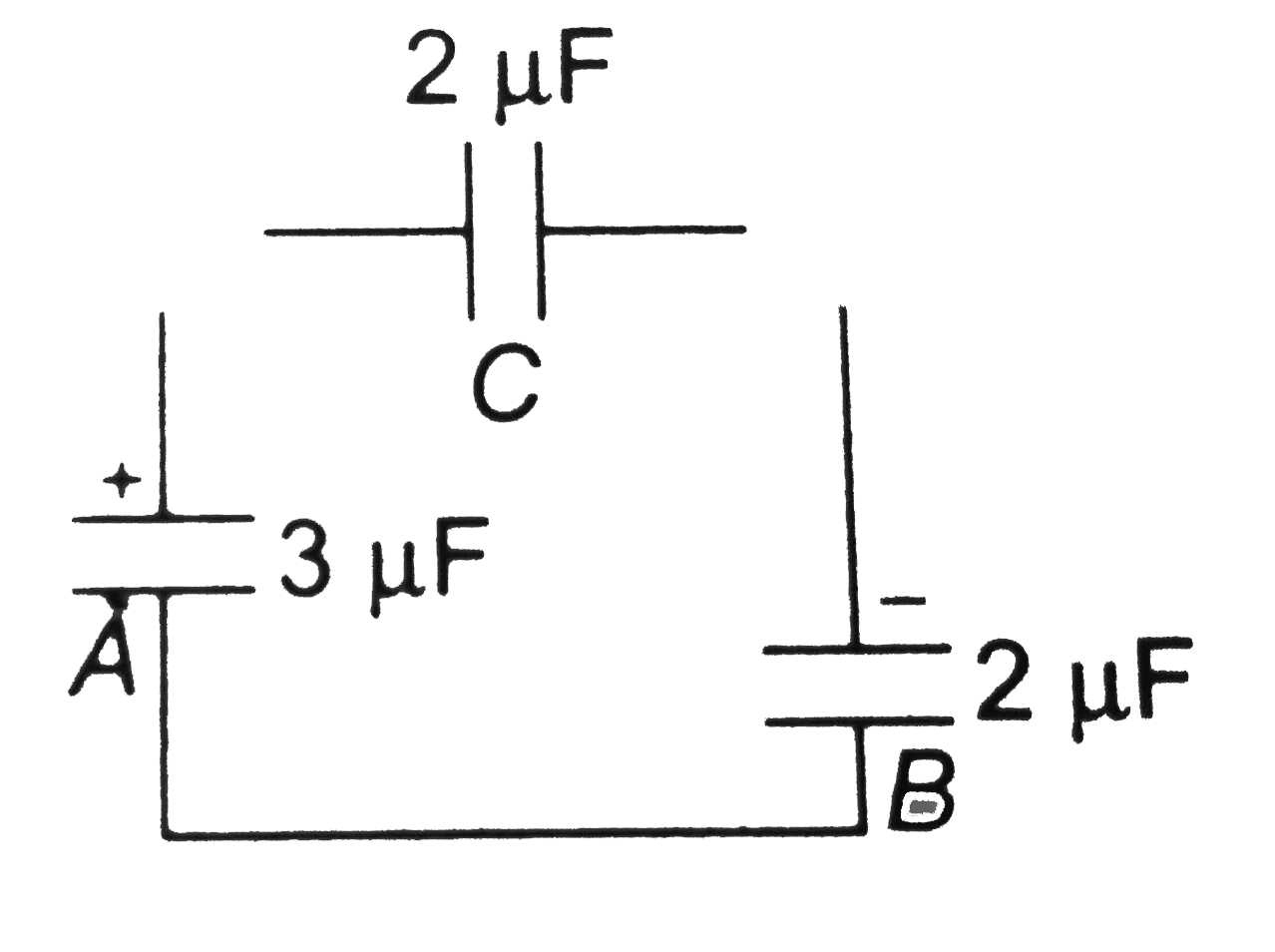
View SolutionTwo capacitors A and B with capacities 3μF and 2μF are charged to a potential difference of 100V and 180V, respectively. The plates of the capacitors are connected as show in figure with one wire of each capacitor free. The upper plate of A is positive and that of B is negastive. An uncharged 2μF capcitor C with lead wires falls on the free ends to complete the circuit. Calculate
a. the final charge on the three capacitors.
b. the amount of electrostatic energy stored in the system before and after completion of the circuit.
View SolutionThree capacitors of capacitances 2μF, 3μF and 6μF are connected in series with a 12 V battery. All the connecting wire are disconnected, the three positive plates are connected together and the three negative plates are connected together. Find the charges on the three capacitors after the reconnection.
View SolutionTwo capacitors of capacitance 2μF and 3μF are joined in series. Outer plate first capacitor is at 1000 volt and outer plate of second capacitor is earthed (grounded). Now the potential on inner plate of each capacitor will be
View Solution
