In a region of space the electric field in the x-direction and proportional to xi.e., →E=E0xˆi. Consider an imaginary cubical volume of edge a with its parallel to the axes of coordinates. The charge inside this volume will be
To find the charge inside a cubical volume in an electric field defined by →E=E0x^i, we can use Gauss's law. Here are the steps to solve the problem:
Step 1: Understand the Electric Field
The electric field is given as →E=E0x^i, which means the electric field varies linearly with the x-coordinate. At any point x, the electric field has a magnitude of E0x and points in the positive x direction.
Step 2: Define the Cubical Volume
Consider a cube with edge length a, positioned such that one of its corners is at the origin (0,0,0) and the opposite corner is at (a,a,a). The cube's faces are parallel to the coordinate axes.
Step 3: Apply Gauss's Law
Gauss's law states that the net electric flux ΦE through a closed surface is equal to the charge Qenc enclosed by that surface divided by the permittivity of free space ϵ0:
ΦE=Qencϵ0
Step 4: Calculate the Electric Flux
The electric flux through a surface is given by:
ΦE=∫→E⋅d→A
For our cube, we need to consider the contributions from the two faces that are perpendicular to the x-axis (the front face at x=a and the back face at x=0).
- Front Face (at x=a):
- Electric field at this face: →E=E0a^i
- Area vector d→A=a2^i
- Contribution to flux:
Φfront=→E⋅d→A=(E0a)⋅(a2)=E0a3
- Back Face (at x=0):
- Electric field at this face: →E=E0⋅0^i=0
- Contribution to flux:
Φback=0
Step 5: Total Electric Flux
The total electric flux through the cube is:
ΦE=Φfront+Φback=E0a3+0=E0a3
Step 6: Relate Flux to Charge
Using Gauss's law:
ΦE=Qencϵ0
Substituting the expression for flux:
E0a3=Qencϵ0
Step 7: Solve for Enclosed Charge
Rearranging gives:
Qenc=E0a3ϵ0
Final Answer
The charge inside the cubical volume is:
Qenc=E0a3ϵ0
---
The electric field is given as →E=E0x^i, which means the electric field varies linearly with the x-coordinate. At any point x, the electric field has a magnitude of E0x and points in the positive x direction.
Consider a cube with edge length a, positioned such that one of its corners is at the origin (0,0,0) and the opposite corner is at (a,a,a). The cube's faces are parallel to the coordinate axes.
Gauss's law states that the net electric flux ΦE through a closed surface is equal to the charge Qenc enclosed by that surface divided by the permittivity of free space ϵ0:
The electric flux through a surface is given by:
- Electric field at this face: →E=E0a^i
- Area vector d→A=a2^i
- Contribution to flux:
Φfront=→E⋅d→A=(E0a)⋅(a2)=E0a3
- Electric field at this face: →E=E0⋅0^i=0
- Contribution to flux:
Φback=0
The total electric flux through the cube is:
ΦE=Φfront+Φback=E0a3+0=E0a3
Using Gauss's law:
ΦE=Qencϵ0
Substituting the expression for flux:
E0a3=Qencϵ0
Rearranging gives:
Qenc=E0a3ϵ0
The charge inside the cubical volume is:
Qenc=E0a3ϵ0
Similar Questions
In a uniform electric field E if we consider an imaginary cubical closed surface of side a, then find the net flux through the cube ?
View SolutionThe electric field in a region is given by →E=E0xˆi. The charge contained inside a cubical volume bounded by the surface x=0, x=2m, y=0, y=2m, z=0 and z=2m is nε0E0. Find the va,ue of n.
View SolutionThe electric field in a region is given by →E=E0axˆi. Find the electric flux passing through a cubical volume bounded by the surfaces x=0,x=a,y=0,y=a,z=0 and z=a.
View SolutionThe electric field in a cubical volume is
→E=E0(1+za)ˆi+E0(za)ˆj
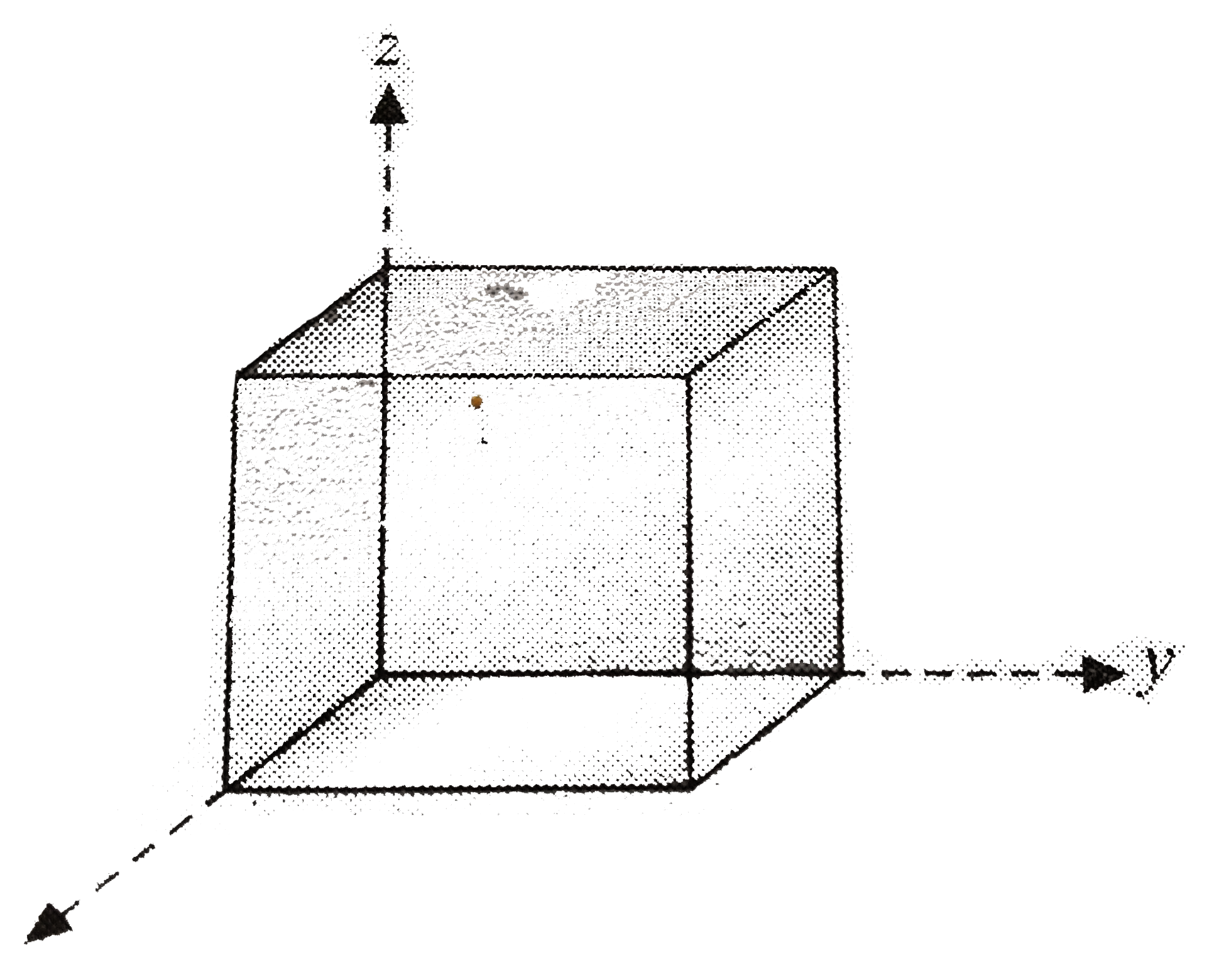
Each edge of the cube measures d, and one of the corners lies at the origin of the coordinates. Determine the net charge within the cube.
View SolutionThe electric field in a region of space is given by, →E=E0ˆi+2E0ˆj where E0=100N/C. The flux of this field through a circular surface of radius 0.02m parallel to the Y-Z plane is nearly.
View SolutionIn a region of space uniform electric field is present as →E=E0ˆi and uniform magnetci field is present as →B=−B0ˆj . An electron is released from rest at origin. What is the path followed by electron after released. (E0&B0are positive constants )
View SolutionElectric field in a region is given by →E=−4xˆi+6yˆj. Then find the charge enclosed in the cube of side 1m oriented as shown in the diagram
View SolutionThe electric field in a region is given by E=E0xlˆi. Find the charge contained inside a cubical 1 volume bounded by the surfaces x=0,x=a,y=0,yh=,z=0 and z=a. Take E0=5×103N/C l=2cm and a=1m.
View SolutionTwo long parallel conducting horizontal rails are connected by a conducting wire at one end. A uniform magnetic field B (directed vertically downwards) exists in the region of space.

A light uniform ring of diameter d which is practically equal to separation between the rails is placed over the rails as shown in Fig. If resistance of ring be (λ) per unit length
The force required to pull the ring with uniform velocity v is
View SolutionThe magnetic field existing in a region is given by →B=B0(1+xl)→k. A square loop of edge l and carrying a current I, is placed with its edges parallel to the x-y axes. Find the magnitude of the net magnetic force experienced by the loop.
View Solution