Two long parallel conducting horizontal rails are connected by a conducting wire at one end. A uniform magnetic field B (directed vertically downwards) exists in the region of space.
A light uniform ring of diameter d which is practically equal to separation between the rails is placed over the rails as shown in Fig. If resistance of ring be (λ) per unit length
The force required to pull the ring with uniform velocity v is
The flux of electric field through the differential cube is zero
The flux of electric field through the cube = 12 dx dy dz
The charge enclosed by the cube is zero.
The charge enclosed by a spherical surface of radius r, centered at origin is 16πε0r3
The correct Answer is:B, D
Step by step video & image solution for Two long parallel conducting horizontal rails are connected by a conducting wire at one end. A uniform magnetic field B (directed vertically downwards) exists in the region of space. A light uniform ring of diameter d which is practically equal to separation between the rails is placed over the rails as shown in Fig. If resistance of ring be (lambda) per unit length The force required to pull the ring with uniform velocity v is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -III ELECTRO FLUX & GAUSS.S LAW) (LEVEL - I (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)3videos
ELECTROSTATICS
- BOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -III ELECTRO FLUX & GAUSS.S LAW) (LEVEL - I (ADVANCED) MATRIX MATCHING TYPE QUESTIONS1videos
ELECTROSTATICS
- BOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -III ELECTRO FLUX & GAUSS.S LAW) (LEVEL - I (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTION)14videos
ELECTROSTATICS
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE13videos
ELECTROMAGNETICS
- BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS10videos
ELEMENTS OF VECTORS
Similar Questions
Two long parallel conducting horizontal rails are connected by a conducting wire at one end. A uniform magnetic field B (directed vertically downwards) exists in the region of space.
A light uniform ring of diameter d which is practically equal to separation between the rails is placed over the rails as shown in Fig. If resistance of ring be (λ) per unit length
The current in the wire MN isView SolutionA small conducting rod of length l, moves with a uniform velocity v in a uniform magnetic field B as shown in fig __
View Solution
Knowledge Check
- Question 1 - Select One
A conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
Ait is rotated about its axis.Bit is rotated about its diameter.Cit is not moved.Dit is given translational motion in the field.
Two parallel fixed conducting rails are l distance apart. They are connected by a conducting wire xy. A uniform magnetic field B is applied normal to its plane. Two other rods PQ and RT(RS = ST) are moved with a constant velocity v. Resistance/ length of these two rods are λ no other wire has resistance. Then :
View SolutionA long conducting wire AH is moved over a conducting triangular wire CDE with a constant velocity v in a uniform magnetic field →B directed into the plane of the paper. Resistance per unit length of each wire is ρ. Then
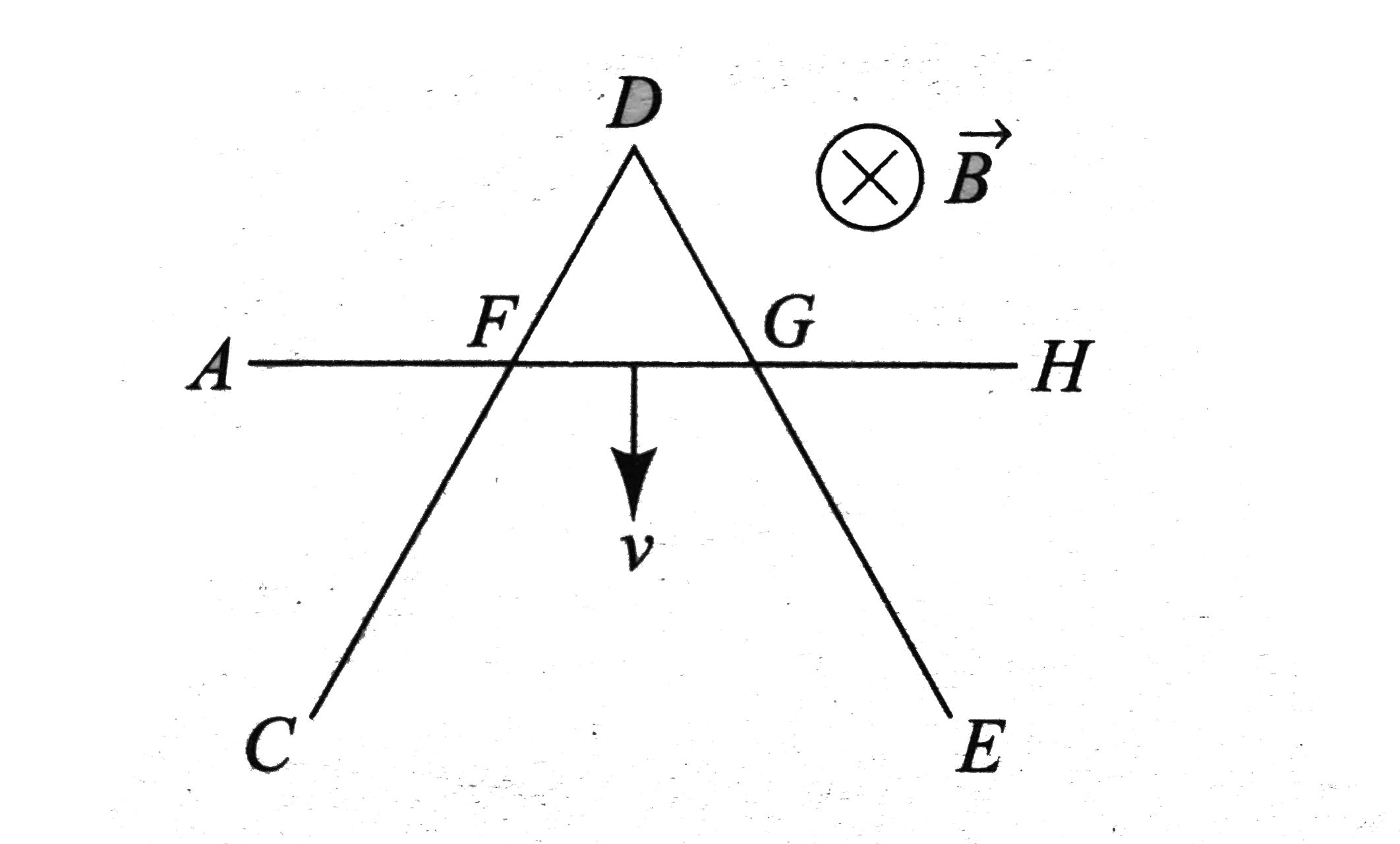View SolutionA semicircle conducting ring of radius R is placed in the xy plane, as shown in Fig. A uniform magnetic field is set up along the x-axis. No emf, will be induced in the ring if
View SolutionTwo parallel resistanceless rails are connected by an inductor of inductance L at one end as shows in Fig. A magnetic field B exists in the space which is perendicular to the plane of the rails. Now a conductor of length l and mass m is placed transverse on the rail and given an inpulse J toward the rightward direction. Then choose the correct option (S).
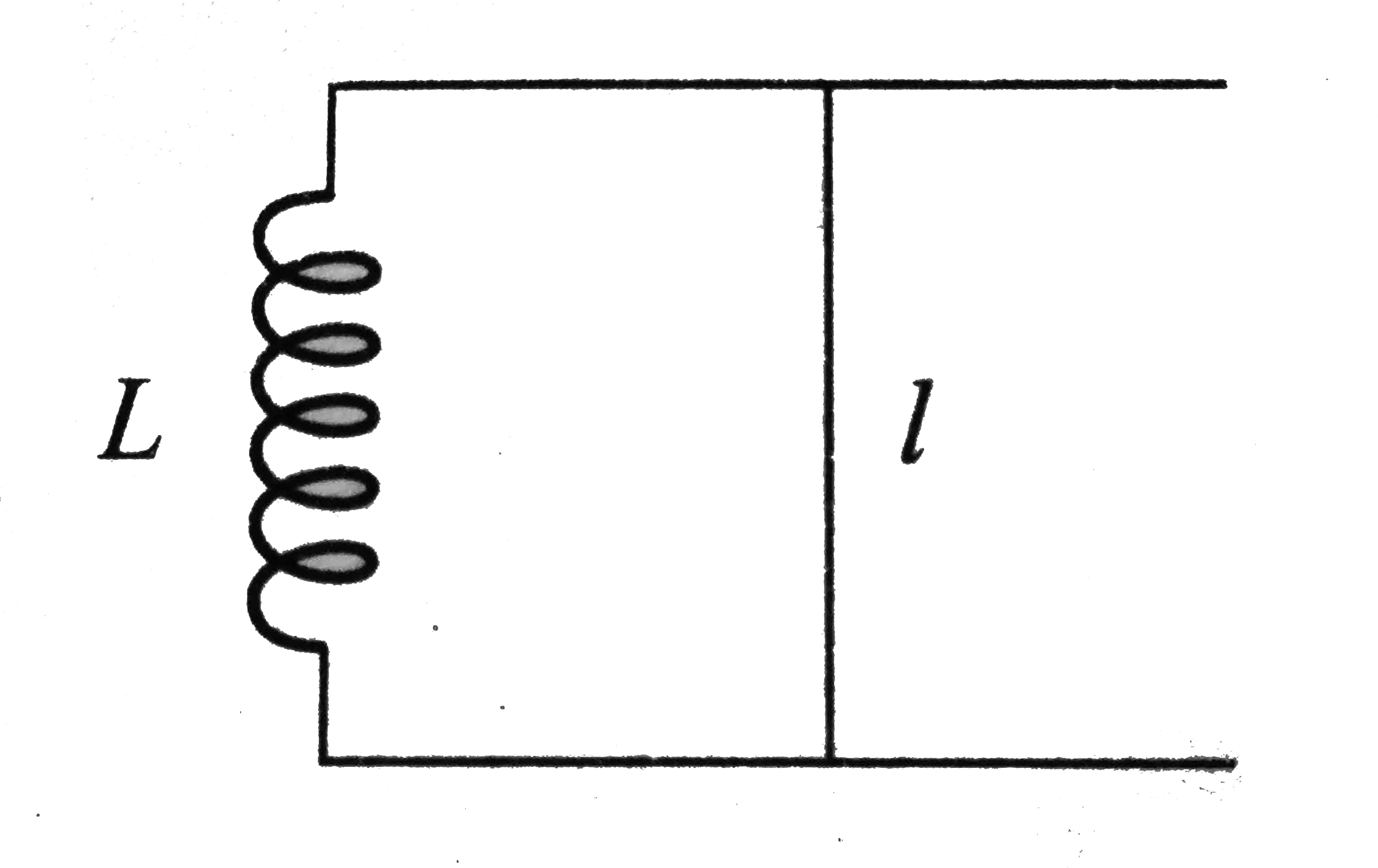View SolutionA pair of parallel conducting rails lie at right angle to a uniform magnetic field of 2.0T as shown in the fig. two resistor 10Ω and 5Ω are to slide without friction along the rail. The distance between the conducting rails is 0.1m. Then
View SolutionShows two long metal rails placed horizontally and parallel to each other at a separation i. A uniform magnetic field b exists in the vertically downward direction. A wire of mass m can slide on the rails. The rails are connected to a constant current source which drives a current I in the circuirt. The friction coefficient between the rails and the wire is μ. (a) What should be the minimum value of μ which can prevent the wire from sliding on the rails? (b) Describe the motion of the wire if the value of μ is half the value found in the previous part.
View Solution
A conducting wire MN carrying a current I is bent into the shape as shown and placed in xy plane. A uniform magnetic field →B=−Bˆk is existing in the region. The net magnetic force experenced by the conducting wire MN isView Solution