In a region of space the electric field in the x-direction and proportional to xi.e., →E=E0xˆi. Consider an imaginary cubical volume of edge a with its sides parallel to the axes of coordinates. The charge inside this volume will be
zero
ε0E0a3
1ε0E0a3
16ε0E0a3
The correct Answer is:b
Field at face ABCD=−E0x0ˆi
Flux over the face ABCD=−E0x0a2
The negative sign arises as the field is directed into the cube.
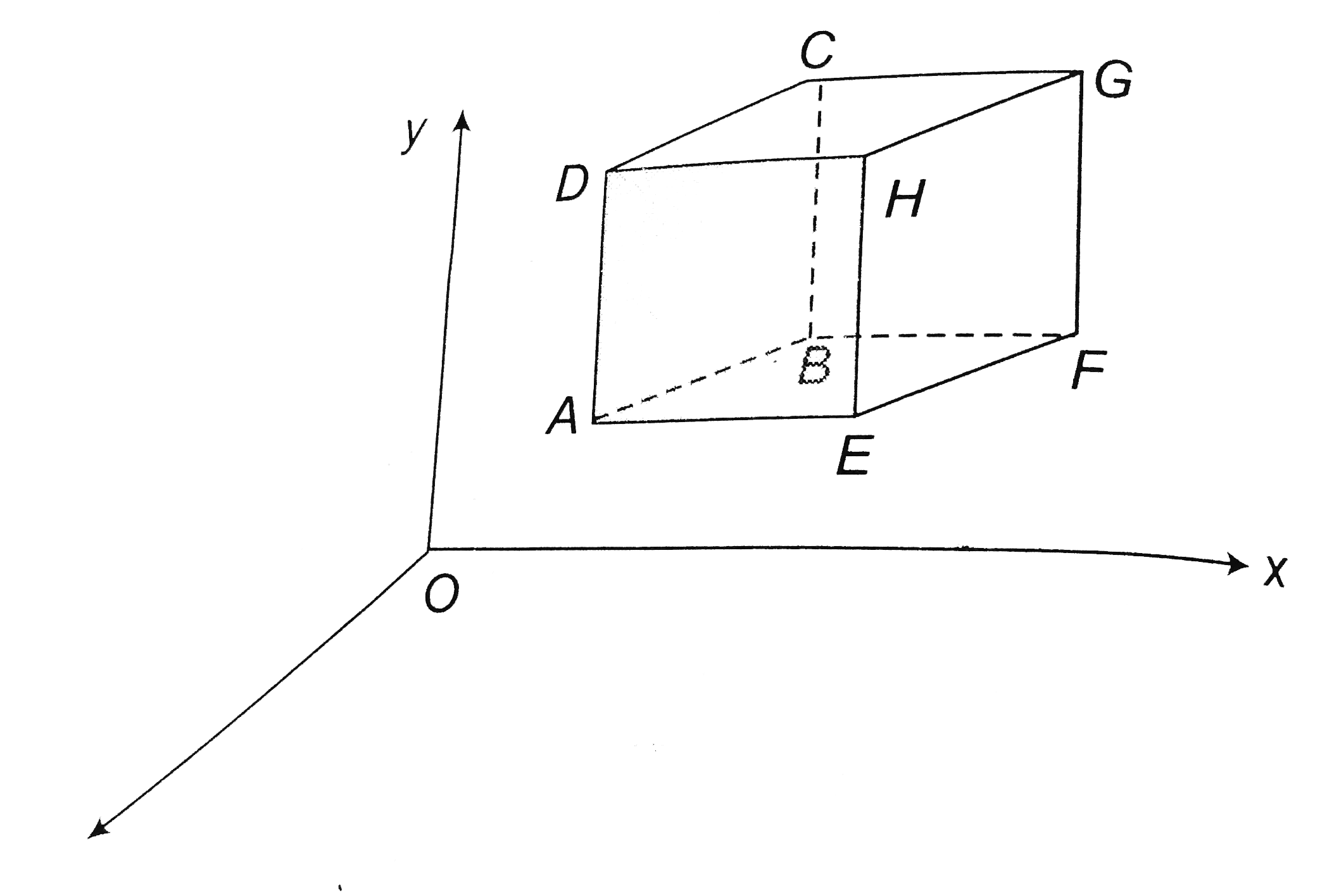
Field at face EFGH=E0(x0+a)ˆi
Flux over the face EFGH=E0(x0+a)a2
Flux over the other four faces is zero as the field is parallel to the surfaces.
Total flux over the cube =E0a3=1ε0q.
Where q si the total charge under the cube
∴q=ε0E0a3.
Topper's Solved these Questions
- ELECTRIC CHARGE, FIELD & FLUXBook:A2ZChapter:ELECTRIC CHARGE, FIELD & FLUXExercise:Electric Dipole
Explore 29 Videos
- ELECTRIC CHARGE, FIELD & FLUXBook:A2ZChapter:ELECTRIC CHARGE, FIELD & FLUXExercise:Problems Based On Mixed Concepts
Explore 40 Videos
- ELECTRIC CHARGE, FIELD & FLUXBook:A2ZChapter:ELECTRIC CHARGE, FIELD & FLUXExercise:Electric Field And Motion
Explore 37 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:A2ZChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Section D - Chapter End Test
Explore 30 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBook:A2ZChapter:ELECTRIC POTENTIAL & CAPACITANCEExercise:Section D - Chapter End Test
Explore 29 Videos
Similar Questions
The electric fields in a region is given by →E=E0xLˆi ,Find the charge contained inside a cubical volume bounded by the surface x=0,x=L,y=0,y=L,z=0,z=L.
View SolutionIn a uniform electric field E if we consider an imaginary cubical closed surface of side a, then find the net flux through the cube ?
View Solution
Knowledge Check
The electric field in a certain region is given by →E=(Kx3)→i. The dimensions of K are -
AMLT−3A−1BML−2T−3A−1CML4T−3A−1Ddimensionless
In a certain region of space the electric field increases radially as →E=90r(−ˆr) .The electric charge contained within a sphere of radius 2m centred at the origin is:
View SolutionThe electric field in a region is given by →E=E0xˆi. The charge contained inside a cubical volume bounded by the surface x=0, x=2m, y=0, y=2m, z=0 and z=2m is nε0E0. Find the va,ue of n.
View SolutionIn a certain region of space, the electric field always pointing in x - direction but its magnitude decreases from E=560N/Cat x=0 to E=410N/C at x=25m if a cubical box of side length I = 25 m is oriented, such that its four sides are parallel to the field lines, then charge enclosed by the box is......
View SolutionThe electric field in a cubical volume is
→E=E0(1+za)ˆi+E0(za)ˆj
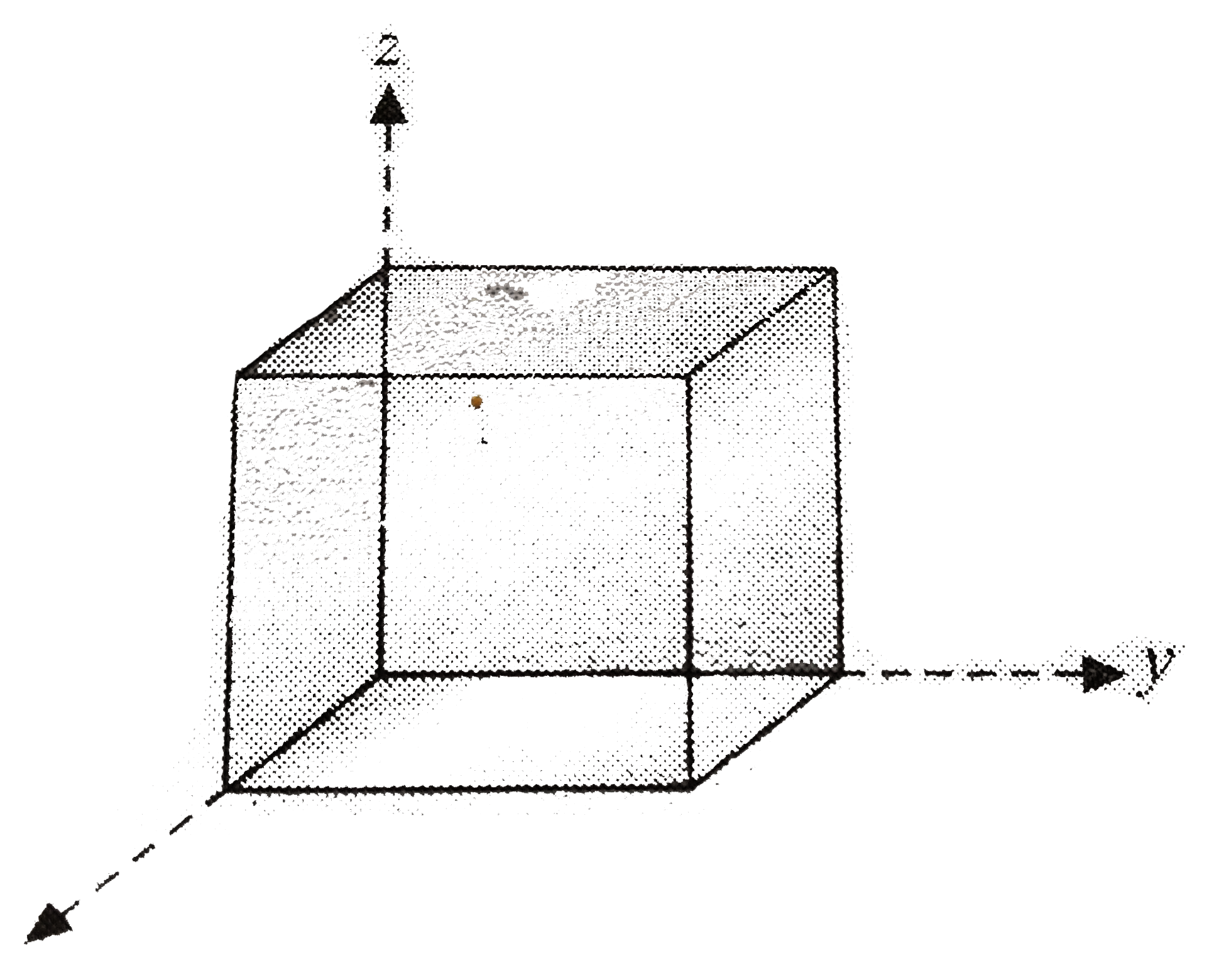
Each edge of the cube measures d, and one of the corners lies at the origin of the coordinates. Determine the net charge within the cube.
View SolutionThe electric field in a region is given by →E=E0axˆi. Find the electric flux passing through a cubical volume bounded by the surfaces x=0,x=a,y=0,y=a,z=0 and z=a.
View SolutionThe electric field in a region of space is given ¯¯¯E=E0ˆi+2E0ˆj where E0=100NC .The flux of this field through a circular surface of radius 0.02m parallel to the Y-Z plane is nearly:
View SolutionThe magnetic field existing in a region is given by →B=B0(1+xl)→k. A square loop of edge l and carrying a current I, is placed with its edges parallel to the x-y axes. Find the magnitude of the net magnetic force experienced by the loop.
View Solution

