The following table gives the current l ( in amperes) through two devies for several values of potential differences V( in volt ) . From these data which does not obey ohm's law ?
To determine which device does not obey Ohm's law, we need to analyze the relationship between the potential difference (V) and the current (I) for both devices. According to Ohm's law, the ratio VI (which represents resistance, R) should remain constant for a device that obeys Ohm's law.
1. List the Data:
- Device 1:
- V1=2V,I1=4.5A
- V2=3V,I2=6.75A
- V3=4V,I3=9A
- Device 2:
- V1=2V,I1=1.5A
- V2=3V,I2=2.2A
- V3=4V,I3=2.8A
2. Calculate the Ratios for Device 1:
- For V=2V,I=4.5A:
R1=V1I1=24.5=49Ω
- For V=3V,I=6.75A:
R2=V2I2=36.75=49Ω
- For V=4V,I=9A:
R3=V3I3=49Ω
3. Calculate the Ratios for Device 2:
- For V=2V,I=1.5A:
R1=V1I1=21.5=43Ω
- For V=3V,I=2.2A:
R2=V2I2=32.2≈1.36Ω
- For V=4V,I=2.8A:
R3=V3I3=42.8≈1.43Ω
4. Analyze the Results:
- For Device 1, the resistance R is constant at 49Ω.
- For Device 2, the resistance values are 43Ω, 1.36Ω, and 1.43Ω. These values are not constant.
5. Conclusion:
- Device 1 obeys Ohm's law as the ratio VI is constant.
- Device 2 does not obey Ohm's law as the ratio VI changes with different values of V and I.
Final Answer:
Device 2 does not obey Ohm's law.
- Device 1:
- V1=2V,I1=4.5A
- V2=3V,I2=6.75A
- V3=4V,I3=9A
- Device 2:
- V1=2V,I1=1.5A
- V2=3V,I2=2.2A
- V3=4V,I3=2.8A
- For V=2V,I=4.5A:
R1=V1I1=24.5=49Ω
- For V=3V,I=6.75A:
R2=V2I2=36.75=49Ω
- For V=4V,I=9A:
R3=V3I3=49Ω
- For V=2V,I=1.5A:
R1=V1I1=21.5=43Ω
- For V=3V,I=2.2A:
R2=V2I2=32.2≈1.36Ω
- For V=4V,I=2.8A:
R3=V3I3=42.8≈1.43Ω
- For Device 1, the resistance R is constant at 49Ω.
- For Device 2, the resistance values are 43Ω, 1.36Ω, and 1.43Ω. These values are not constant.
- Device 1 obeys Ohm's law as the ratio VI is constant.
- Device 2 does not obey Ohm's law as the ratio VI changes with different values of V and I.
Device 2 does not obey Ohm's law.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:AAKASH INSTITUTE ENGLISHChapter:CURRENT ELECTRICITYExercise:Try Yourself
Explore 34 Videos
- CURRENT ELECTRICITYBook:AAKASH INSTITUTE ENGLISHChapter:CURRENT ELECTRICITYExercise:ASSIGNMENT(SECTION-A(OBJECTIVE TYPE QUESTIONS))
Explore 69 Videos
- COMMUNICATION SYSTEMS Book:AAKASH INSTITUTE ENGLISHChapter:COMMUNICATION SYSTEMS Exercise:ASSIGNMENT SECTION D (Assertion-Reason)
Explore 10 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:AAKASH INSTITUTE ENGLISHChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:ASSIGNMENT (SECTION-D)
Explore 10 Videos
Similar Questions
When a current of (2.5±0.5) ampere flows through a wire, it develops a potential difference of (20±1) volt, the resistance of the wire is
View SolutionThe following table gives the length of three copper rods, their diameters, and the potential differences between their ends. Rank the rods according to (a) the magnitude of the electric field within them, (b) the current density within them, and (c ) the drift speed of electrons through them, greates first.

View SolutionA current of (2.5±0.05) A flows through a wire and develops a potential difference of (10±0.1) volt. Resistance of th wire in ohm, is
View SolutionA current of (2.5±0.05) A flows through a wire and develops a potential difference of (10±0.07) volt. Resistance of the wire in ohm, is
View SolutionThe values of current (I) flowng through a given resistor of resistance (R ), for the corresponding values of potential difference (V) across the resistor are as given below :

Plot a graph between current (I) and potential difference (V) and determine the resistance (R ) of the resistor.
View SolutionA part of a complete circuit is shown in the figure . At some instant the value of current I is 1 A and it is decreasing at a rate of 102As−1 . The value of the potential difference VP−VQ, (in volts) at that instant , is ____________.
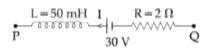
View SolutionIf V is the potential difference between the ends of conductor and l is the current through it, then ohm's law states that
View SolutionAn α−particle is accelerated through a potential difference of V volts from rest. The de-Broglie's wavelengths associated with it is.
View SolutionAn α−particle is accelerated through a potential difference of V volts from rest. The de-Broglie's wavelengths associated with it is.
View SolutionThe circuit shown in the figure is a series LCR circuit connected to an AC source. This circuit has many important applications in practical electronic systems. In the given circuit, L=20mH and frequency of applied alternating potential difference is ω=8000rad/s. Initial phase of applied potential difference has such a minimum value that initial value of instantaneous potential difference is half of is peak value while initial phase of current in the circuit has such a minimum value that initial value of instantaneous current equals its peak value. We also observe that current in the circuit leads the net voltage across the circuit. It is given that peak values of potential difference across R and L are I VR(peak))=25V
V(L)peak=20V
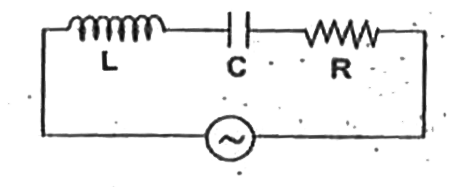
rms value of potential difference across capacitor is nearly
View Solution
