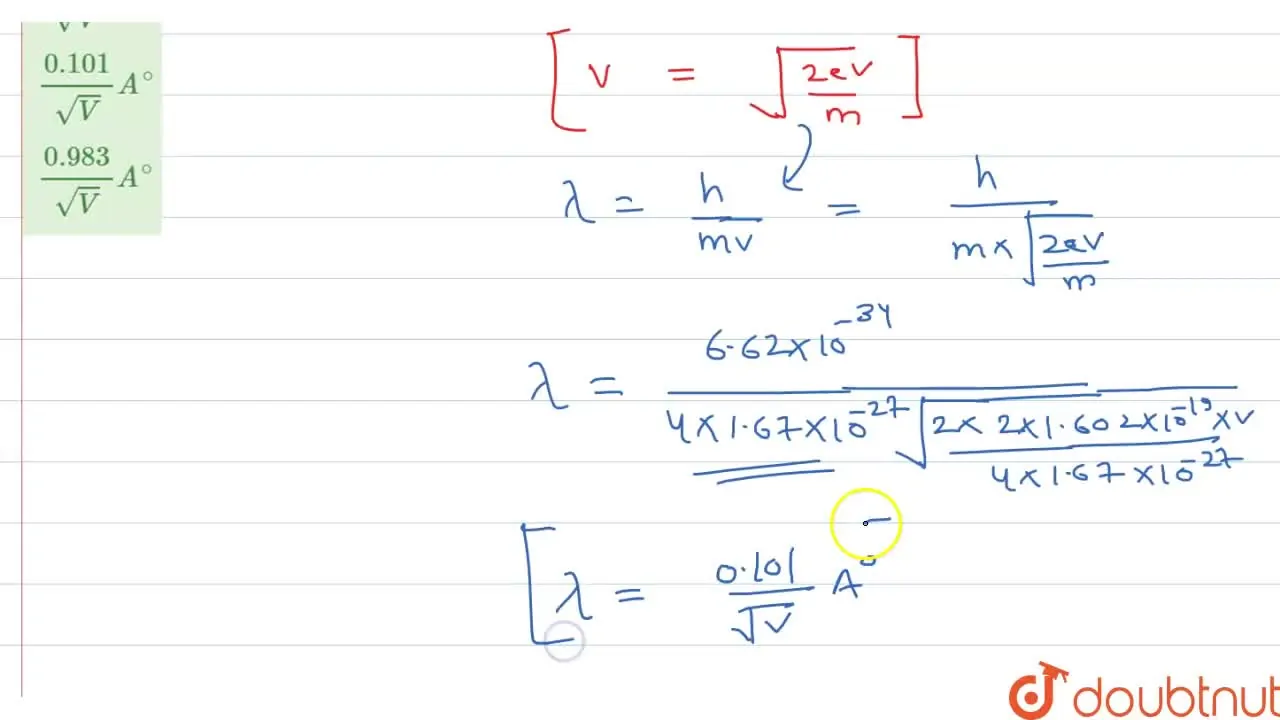
An α−particle is accelerated through a potential difference of V volts from rest. The de-Broglie's wavelengths associated with it is.
√150VA∘
0.286√VA∘
0.101√VA∘
0.983√VA∘
The correct Answer is:C
Step by step video & image solution for An alpha-"particle" is accelerated through a potential difference of V volts from rest. The de-Broglie's wavelengths associated with it is. by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - ALLENCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercise - 0259videos
ATOMIC STRUCTURE
- BOOK - ALLENCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercise - 0321videos
ATOMIC STRUCTURE
- BOOK - ALLENCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercise - 05[A]14videos
ATOMIC STRUCTURE
- BOOK - ALLENCHAPTER - IUPAC NOMENCLATUREEXERCISE - Exercise - 05(B)7videos
IUPAC NOMENCLATURE
Similar Questions
The de Broglie wavelength associated with particle is
View SolutionAn electron is accelerated through a potential difference of V volit .Find th e de Broglie wavelength associated with electron.
View SolutionAn electron is accelerated by a potential difference of 9.375 V . Find the de-Broglie wavelength associated with it is Å
View SolutionAn α - particle is accelerated through a potential difference of 100 V. Its de-Broglie's wavelength is
View SolutionAn electron is accelerated through a potential difference of 100 volts. What is the de-Broglie wavelength associated with it ? To which part of the electromagnetic does this value of wavelength correspond ?
View SolutionAn electron is accelerated through a potential difference of 64volts. What is the de-broglie wavelength associated with it? To which part of the electromagnetic spectrum does this value of wavelength correspond?
View SolutionA chemist was performing an experiment to study the effect of varying voltage and de-Broglie wavelength of the electron. In first experiment, the electron was accelerated through a potential difference of 1 kV from rest and in second experiment, it was accelerated through a potential difference of 2 kV from rest. The wavelength of de-Broglie waves associated with electron is given by
λ=h√2qVm
Where, V is the voltage through which one electron is accelerated
Putting the values of h, m and q, we get
λ=12.3√VÅ
Answer the following question
In order of get half velocity of electron than in second case , the applied potential difference from rest will be :View SolutionA chemist was performing an experiment to study the effect of varying voltage and de-Broglie wavelength of the electron. In first experiment, the electron was accelerated through a potential difference of 1 kV from rest and in second experiment, it was accelerated through a potential difference of 2 kV from rest.
The wavelength of de-Broglie waves associated with electron is given by
λ=h√2qVm
Where, V is the voltage through which one electron is accelerated
Putting the values of h, m and q, we get
λ=12.3√VÅ
Answer the following question
The wavelength of electron will be :View SolutionAn electron is accelerated through a potential difference of 100 V , then de-Broglie wavelength associated with it is approximately_____. A∘
View SolutionAn electron is accelerated by a potential difference of 25 V. Find the de Broglie wavelength associated with it.
View Solution