In Gauss's law ε0∮→E.¯¯¯¯ds=Qenclosed, is →E only due to charges enclosed ?
To answer the question, "In Gauss's law, is the electric field (E) only due to charges enclosed?", we can break down the explanation step by step:
1. Understanding Gauss's Law:
Gauss's law states that the electric flux (Φ) through a closed surface is proportional to the charge (Q_enclosed) enclosed within that surface. Mathematically, it is expressed as:
Φ=∮→E⋅d→s=Qenclosedϵ0
2. Defining Electric Flux:
The electric flux (Φ) is defined as the integral of the electric field (E) over a closed surface (S). This means that the total flux through the surface is determined by the electric field lines passing through it.
3. Analyzing the Electric Field:
The electric field (E) at any point in space can be influenced by all charges present in the vicinity, not just those enclosed by the surface. Therefore, while calculating the electric field at a point, we must consider contributions from both enclosed and external charges.
4. Example Scenario:
Imagine a closed surface surrounding a charge Q_enclosed. If there is another charge Q2 outside this surface, the electric field at a point on the surface will be influenced by both Q_enclosed and Q2. However, the flux through the surface will only depend on Q_enclosed.
5. Conclusion:
To directly answer the question: No, the electric field (E) is not only due to the charges enclosed. It can also be affected by charges that are outside the closed surface.
Summary:
- The electric field (E) at a point is influenced by all nearby charges, both enclosed and external.
- The electric flux through a closed surface, however, is solely due to the charge enclosed within that surface.
Gauss's law states that the electric flux (Φ) through a closed surface is proportional to the charge (Q_enclosed) enclosed within that surface. Mathematically, it is expressed as:
Φ=∮→E⋅d→s=Qenclosedϵ0
The electric flux (Φ) is defined as the integral of the electric field (E) over a closed surface (S). This means that the total flux through the surface is determined by the electric field lines passing through it.
The electric field (E) at any point in space can be influenced by all charges present in the vicinity, not just those enclosed by the surface. Therefore, while calculating the electric field at a point, we must consider contributions from both enclosed and external charges.
Imagine a closed surface surrounding a charge Q_enclosed. If there is another charge Q2 outside this surface, the electric field at a point on the surface will be influenced by both Q_enclosed and Q2. However, the flux through the surface will only depend on Q_enclosed.
To directly answer the question: No, the electric field (E) is not only due to the charges enclosed. It can also be affected by charges that are outside the closed surface.
- The electric field (E) at a point is influenced by all nearby charges, both enclosed and external.
- The electric flux through a closed surface, however, is solely due to the charge enclosed within that surface.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS Book:AAKASH INSTITUTE ENGLISHChapter:ELECTRIC CHARGES AND FIELDS Exercise:TRY YOURSELF
Explore 33 Videos
- ELECTRIC CHARGES AND FIELDS Book:AAKASH INSTITUTE ENGLISHChapter:ELECTRIC CHARGES AND FIELDS Exercise:ASSIGNMENT(SECTION-A) Objective Type Question
Explore 45 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:AAKASH INSTITUTE ENGLISHChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:ASSIGNMENT (SECTION-D)
Explore 10 Videos
- ELECTROMAGNETIC INDUCTIONBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:ASSIGNMENT(SECTION -D) Assertion-Reason type Question)
Explore 15 Videos
Similar Questions
Statement - 1 : If a concentric spheerical Gaussian surface is drawn inside thin spheical shell charge, electric field (E) at each point of surface must be zero.
Statement - 2 : In accordance with Gauss's law
ϕE=∮→E.d→A=Qnet enclosedε0
Qnet enclosed=0 implies ϕE=0
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
A Gaussian surface encloses two of the four positively charged particles. The particles that contribute to the electric field at a point P on the surface are
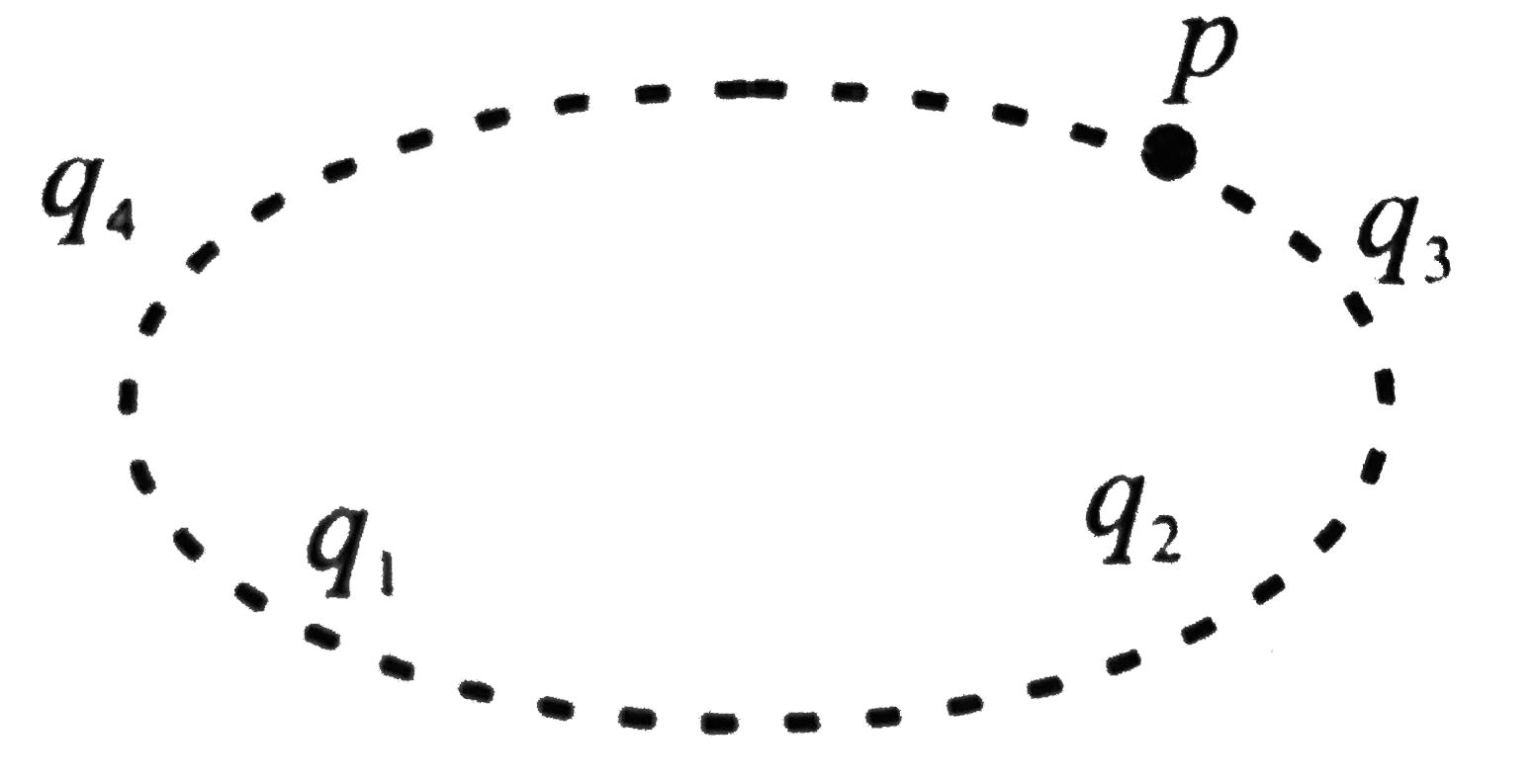
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
If the charge q3 and q4 are displaced (always remaining outside the Gaussian surface), then consider the following two statements :
A: Electric field at each point on the Gaussian surface will remain same .
B: The value of ∮→E.d→A for the Gaussian surface will remain same.
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
The net flux of the electric field through the surface due to q3 and q4 is
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when qencl is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
The net flux of the electric field through the surface is
View Solutionfive charge q1,q2,q3,q4and q5 are fixed at their positions as shown in figure .s is Gaussian surface .The Gauss's law is given by ∮→E.→ds=qε0
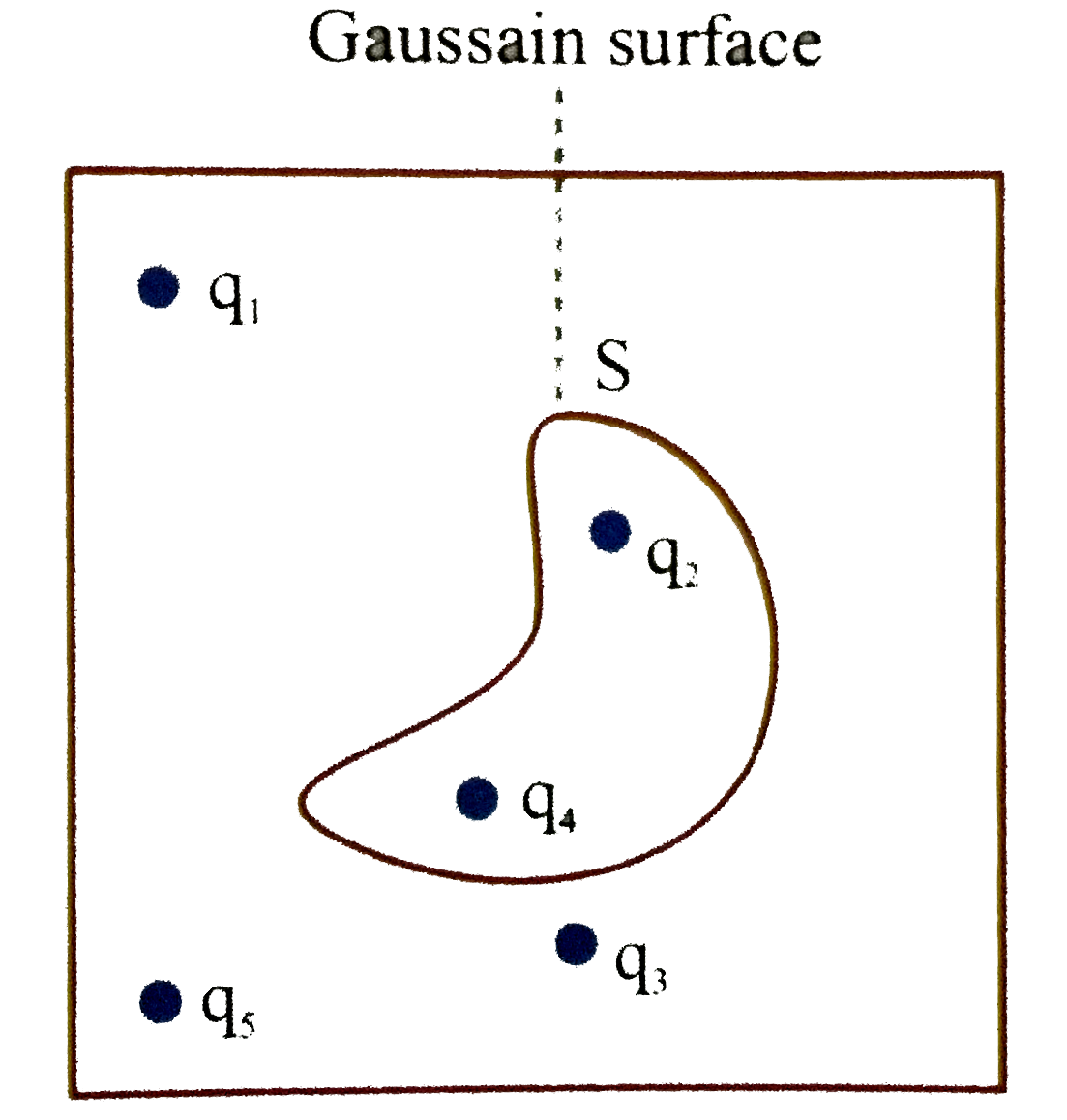
Which of the following statement is correct?
View SolutionGauss.s law is true only if force due to a charge varies as:
View SolutionSTATEMENT -1 : If ∮→E.¯¯¯¯ds over a closed surface is negative,it means the surface encloses a net negative charge.
STATEMENT-2 : We may have a Gaussian surface in which three lines enter and five field lines are coming out.
STATEMENT-3 : The quantity ∮→E.¯¯¯¯ds is independent of the charge distribution inside the surface.
View SolutionFigure shows a conducting sphere with a cavity. A point charge q1 is placed inside cavity, and q2 is placed out side the sphere →Ein is electric field due to charge induced on surface of cavity. →Eout is electric field due to charge induced on outer surface of sphere and →Enet is net field at any point. Two closed gaussian surface S1 & S2 are also drawn in the figure.

View Solution(a) Use Gauss's law to derive the expression for the electric filed (→E) due to straight uniformaly charges infinite line of charges density λC/m.
(b) Draw a graph to show the variation of E with perpendicular from the line of charge.
(c) Find the work done in brining a charge q from prependicular distance r1 to r2(r2>r1).
View Solution