Question

Gauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ${\epsilon }_0\varphi =q_{encl}$,when $q\left(encl\right)$ is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
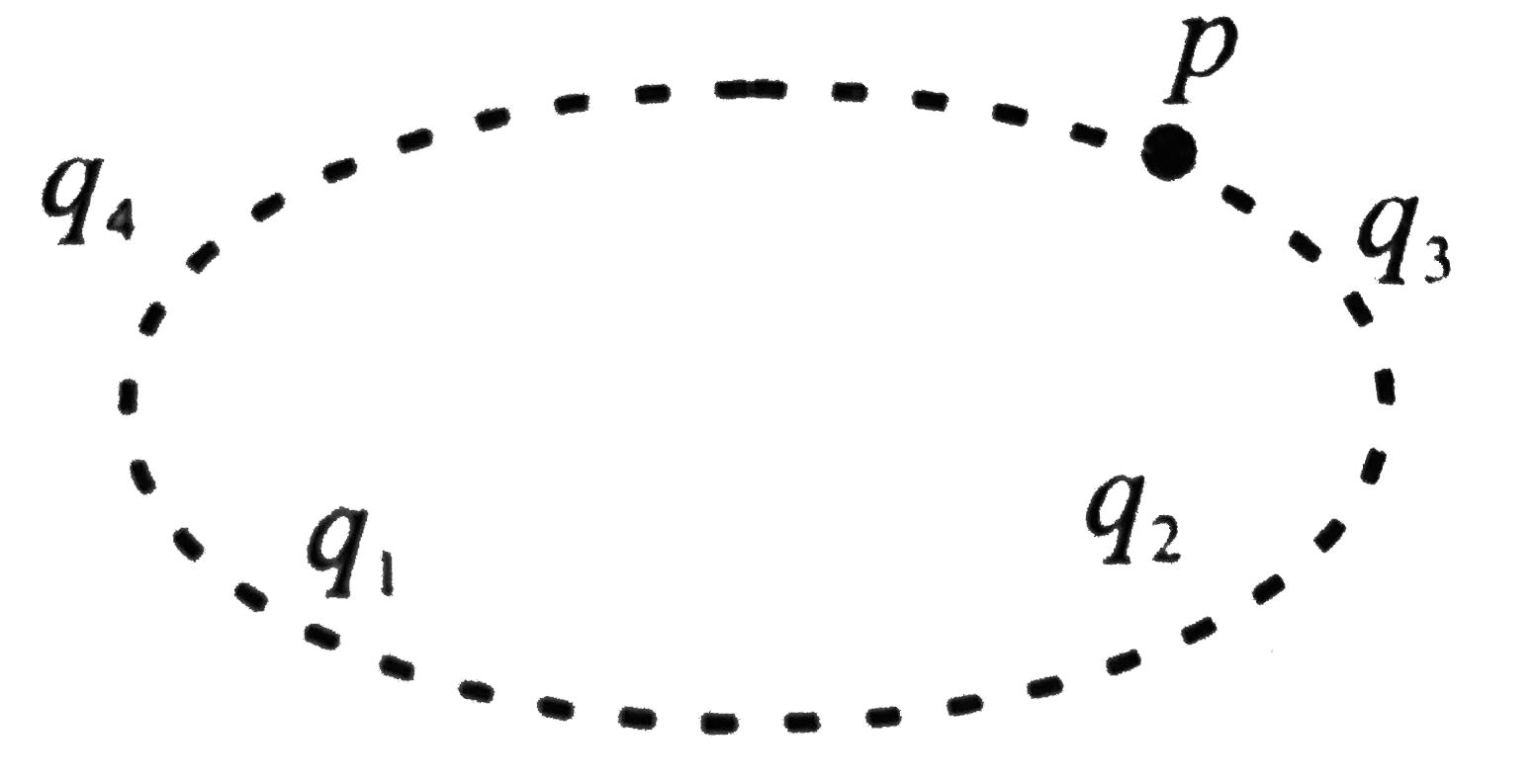
If the charge $q_3$ and $q_4$ are displaced (always remaining outside the Gaussian surface), then consider the following two statements :
$A$: Electric field at each point on the Gaussian surface will remain same .
$B$: The value of $\oint \overrightarrow{E}.d\overrightarrow{A}$ for the Gaussian surface will remain same.

Options

A. Both `A` and `B` are true .
B. Both `A` and `B` are false.
C. `A` is true , but `b` is false.
D. `B` is true , but `A` is false.

Answer

D

Explanation

To solve the problem, we need to analyze the two statements given in the context of Gauss's law and the effect of moving charges outside a Gaussian surface.

1. Understanding Gauss's Law: Gauss's law states that the electric flux (Φ) through a closed surface is proportional to the charge (q_encl) enclosed within that surface. Mathematically, it is expressed as:
\( \epsilon_0 \Phi = q_{encl} \)
where \( \epsilon_0 \) is the permittivity of free space.

2. Identifying the Charges: In this problem, we have charges \( q_3 \) and \( q_4 \) that are located outside the Gaussian surface. The charges that are inside the Gaussian surface are \( q_1 \) and \( q_2 \).

3. Analyzing Statement A:
- Statement A claims that the electric field at each point on the Gaussian surface will remain the same when \( q_3 \) and \( q_4 \) are displaced.
- Since the electric field due to a point charge is given by \( E = \frac{1}{4 \pi \epsilon_0} \frac{q}{r^2} \), moving \( q_3 \) and \( q_4 \) will change the distance \( r \) from these charges to points on the Gaussian surface.
- Therefore, the electric field at points on the Gaussian surface will vary as the positions of \( q_3 \) and \( q_4 \) change. Thus, Statement A is false.

4. Analyzing Statement B:
- Statement B claims that the value of \( \oint \vec{E} \cdot d\vec{A} \) for the Gaussian surface will remain the same.
- The integral \( \oint \vec{E} \cdot d\vec{A} \) represents the electric flux through the Gaussian surface. According to Gauss's law, this flux depends only on the charge enclosed within the surface.
- Since \( q_3 \) and \( q_4 \) are outside the Gaussian surface, their displacement does not affect the enclosed charge \( q_1 + q_2 \). Therefore, the electric flux through the Gaussian surface remains unchanged. Thus, Statement B is true.

Final Conclusion:
- Statement A: False
- Statement B: True