A solid of density 2.5 kg m−3 floats in a fluid with one-third of its volume immersed in it. What is the density of the fluid?
To solve the problem, we need to use the principle of buoyancy, which states that the buoyant force acting on a submerged object is equal to the weight of the fluid displaced by the object. Here's a step-by-step solution:
Step 1: Understand the Given Data
- Density of the solid (ρB) = 2.5 kg/m³
- Volume of the solid (V) = V (unknown)
- Volume of the solid submerged in the fluid = 13V
Step 2: Write the Equation for Buoyant Force
The buoyant force (Fb) acting on the solid is given by:
Fb=ρF⋅Vsubmerged⋅g
Where:
- ρF = density of the fluid (unknown)
- Vsubmerged=13V
- g = acceleration due to gravity (we can cancel it out later)
Step 3: Write the Equation for Weight of the Solid
The weight (W) of the solid is given by:
W=ρB⋅V⋅g
Where:
- ρB=2.5 kg/m³
Step 4: Set Up the Equation for Equilibrium
Since the solid is floating, the buoyant force is equal to the weight of the solid:
ρF⋅(13V)⋅g=ρB⋅V⋅g
Step 5: Cancel Out Common Terms
We can cancel g and V (assuming V≠0):
ρF⋅13=ρB
Step 6: Solve for the Density of the Fluid
Now, substituting the value of ρB:
ρF⋅13=2.5
Multiplying both sides by 3:
ρF=3⋅2.5=7.5 kg/m3
Final Answer
The density of the fluid (ρF) is:
ρF=7.5 kg/m3
---
- Density of the solid (ρB) = 2.5 kg/m³
- Volume of the solid (V) = V (unknown)
- Volume of the solid submerged in the fluid = 13V
The buoyant force (Fb) acting on the solid is given by:
Fb=ρF⋅Vsubmerged⋅g
Where:
- ρF = density of the fluid (unknown)
- Vsubmerged=13V
- g = acceleration due to gravity (we can cancel it out later)
The weight (W) of the solid is given by:
W=ρB⋅V⋅g
Where:
- ρB=2.5 kg/m³
Since the solid is floating, the buoyant force is equal to the weight of the solid:
ρF⋅(13V)⋅g=ρB⋅V⋅g
We can cancel g and V (assuming V≠0):
ρF⋅13=ρB
Now, substituting the value of ρB:
ρF⋅13=2.5
Multiplying both sides by 3:
ρF=3⋅2.5=7.5 kg/m3
The density of the fluid (ρF) is:
ρF=7.5 kg/m3
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:SECTION - A
Explore 50 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:SECTION - B
Explore 23 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:SECTION - J
Explore 9 Videos
- MAGNETISM AND MATTER Book:AAKASH INSTITUTE ENGLISHChapter:MAGNETISM AND MATTER Exercise:ASSIGNMENT (SECTION D)
Explore 26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Assignment(Section-D)
Explore 14 Videos
Similar Questions
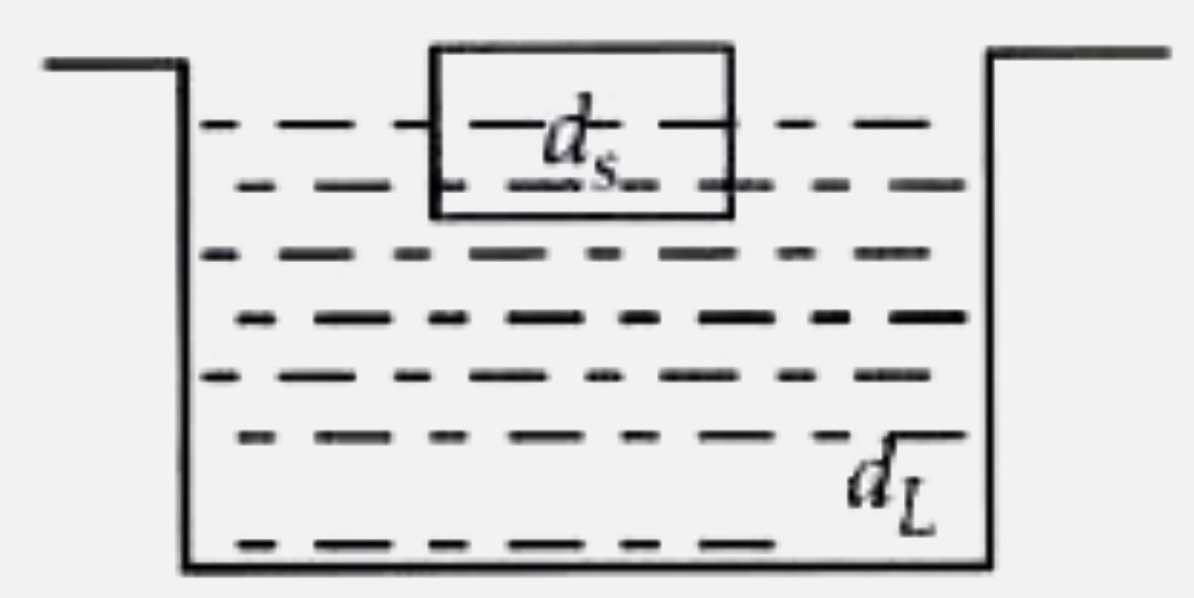
The figure above shows a solid of density dS floating in a liquid of density dL.
The same solid floats in water with 3th5 of its volume immersed in it. Calculate the density of the solid. (density of water = 1 g cm−3 )
View SolutionA block of density ρ floats in a liquid with its one third volume immersed. The density of the liquid is
View SolutionA body floats in water with its one-third volume above the surface. The same body floats in a liquid with one-third volume immersed. The density of the liquid is
View SolutionA body P floats in water with half its volume immersed. Another body Q floats in a liquid of density 34th of the density of water with two - third of the volume immersed. The ratio of density of P to that of Q is
View SolutionA block of wood of volume 25cm3 floats on water with 20cm3 of its volume immersed. Calculate (i) the density, and (ii) the weight of block of wood.
View SolutionA wooden block floats in water with two third of its volume submerged. A. Calculate the density of wood.b. When the same block is placed in oil, three - quarter of its volume in immersed in oil. Calculate the density of oil.
View SolutionA body of density ρ floats with volume V1 of its total volume V immersed in a liquid of density ρ1 and with the remainder of volume V2 immersed in another liquid of density ρ2 where ρ1>ρ2. Find the volume immersed in two liquids. (V1 and V2).
View SolutionA uniform cube of mass M is floating on the surface of a liquid with three fourth of its volume immersed in the liquid (density=ρ). The length of the side of the cube is equal to

View SolutionA rubber ball floats on water with its 1/3 rd volume outside water. What is the density of rubber?
View SolutionA block of wood of volume 30cm3 floats it water with 20cm3 of its volume immersed.
Calculate the density.
View Solution