A tank containing water has an orifice 2 m below the surface of water. If there is no wastage of energy. Find the speed of discharge.
To find the speed of discharge from an orifice located 2 meters below the surface of water in a tank, we can use Bernoulli's principle. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have a tank filled with water, and there is an orifice located 2 meters below the water surface. The pressure at the surface of the water is atmospheric pressure (P0), and we need to find the speed of the water as it exits the orifice.
Step 2: Apply Bernoulli's Equation
According to Bernoulli's principle, for two points in a fluid flow, the following equation holds:
P1+12ρV21+ρgh1=P2+12ρV22+ρgh2
Where:
- P1 and P2 are the pressures at points 1 and 2.
- ρ is the density of the fluid (water in this case).
- V1 and V2 are the velocities at points 1 and 2.
- g is the acceleration due to gravity.
- h1 and h2 are the heights at points 1 and 2.
Step 3: Define the Points
- Point 1: At the surface of the water (height = 2 m)
- Point 2: At the orifice (height = 0 m)
Step 4: Assign Values
- P1=P0 (atmospheric pressure)
- V1=0 (velocity of water at the surface is negligible)
- h1=2 m
- P2=P0 (pressure at the orifice)
- V2=V (velocity at the orifice, which we need to find)
- h2=0 m
Step 5: Substitute into Bernoulli's Equation
Substituting the values into Bernoulli's equation:
P0+0+ρg(2)=P0+12ρV2+0
Step 6: Simplify the Equation
Since P0 appears on both sides, we can cancel it out:
ρg(2)=12ρV2
Step 7: Cancel the Density
We can cancel ρ from both sides (assuming it is not zero):
g(2)=12V2
Step 8: Solve for V
Multiply both sides by 2:
2g(2)=V2
V2=4g
Now take the square root:
V=√4g
Step 9: Substitute the Value of g
Using g≈9.81m/s2:
V=√4×9.81
V=√39.24
V≈6.26m/s
Final Answer
The speed of discharge from the orifice is approximately 6.26 m/s.
---
We have a tank filled with water, and there is an orifice located 2 meters below the water surface. The pressure at the surface of the water is atmospheric pressure (P0), and we need to find the speed of the water as it exits the orifice.
According to Bernoulli's principle, for two points in a fluid flow, the following equation holds:
- P1 and P2 are the pressures at points 1 and 2.
- ρ is the density of the fluid (water in this case).
- V1 and V2 are the velocities at points 1 and 2.
- g is the acceleration due to gravity.
- h1 and h2 are the heights at points 1 and 2.
- Point 1: At the surface of the water (height = 2 m)
- Point 2: At the orifice (height = 0 m)
- P1=P0 (atmospheric pressure)
- V1=0 (velocity of water at the surface is negligible)
- h1=2 m
- P2=P0 (pressure at the orifice)
- V2=V (velocity at the orifice, which we need to find)
- h2=0 m
Substituting the values into Bernoulli's equation:
Since P0 appears on both sides, we can cancel it out:
We can cancel ρ from both sides (assuming it is not zero):
Multiply both sides by 2:
Using g≈9.81m/s2:
The speed of discharge from the orifice is approximately 6.26 m/s.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - A
50 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - B
23 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J
9 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-D)
14 Videos
Similar Questions
Knowledge Check
A small bulb (assumed to be a point source) is placed at the bottom of a tank containing water to a depth of 80cm. Find out the area of the surface of water through which light from the bulb can emerge. Take the value of refractive index of water to be 4/3.
A2.6m2B3.6m2C4.2m2D5.8m2
A tank containing water has an orifice in one vertical side. If the centre of orifice is 4.9 m below the surface level in the tank, the velocity of discharge is:
View SolutionAn under water swimmer is at a depth of 12 m below the surface of water. A bird is at a height of 18 m from the surface of water, directly above his eyes. For the swimmer the bird appears to be at a distance from the surface of water equal to (Refractive Index of water is 4/3)
View SolutionA small bulb (assumed to be a point source) is placed at the bottom of a tank containing water to a depth of 80cm. Find out the area of the surface of water through which light from the bulb can emerge. Take the value of refractive index of water to be 4/3.
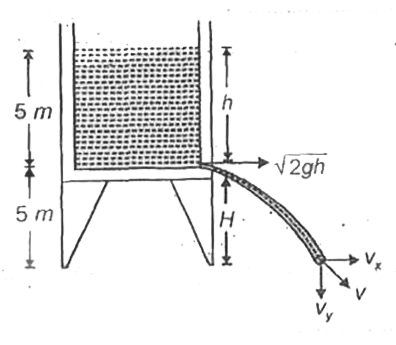
View SolutionA water tank is placed on a platform of height 5 m high and there is an orifice near the bottom in the wall of tank at 5 m below the level of water. Find the speed with which water will hit the ground [Take g = 10 m/s2 ]
View SolutionWater is filled in a rectangular tank of size 3m×2m×1m. a) Find the total force exerted by the water on the bottom surface of the tank. b) Consider a vertical side of area 2m×1m. Take a horizontal strip of wide δx metre in this side, situated at a depth of x metre from the surface of water.Find the force by the water on this strip. c) Find the torque of the force calculate in part b) about the bottom edge of this side. d) Find the total force by the water on this side. e) Find the total torque by the water on the side about the bottom edge. neglect the atmospheric pressure and take =10ms−2.
View SolutionA boat carrying steel balls is floating on the surface of water in a tank. If the balls are thrown into the tank one by one, how will it affect the level of water ?
View SolutionHeight of a tank in the form of an inverted cone is 10 m and radius of its circular base is 2 m. The tank contains water and it is leaking through a hole at its vertex at the rate of 0.02m3/s. Find the rate at which the water level changes and the rate at which the radius of water surface changes when height of water level is 5 m.
View Solution
