Find the total pressure inside a sperical air bubble of radius 0.2 mm. The bubble is at a depth 5 cm below the surface of a liquid of density kg and surface tension 0.082 N . (Given : atmospheric pressure = 1.01 )
Hint :
= atmospheric pressure + gauge pressure of liquid column.
To find the total pressure inside a spherical air bubble at a certain depth in a liquid, we can use the formula:
Pi=Po+2SR
Where:
- Pi is the total pressure inside the bubble.
- Po is the pressure exerted on the bubble from the outside.
- S is the surface tension of the liquid.
- R is the radius of the bubble.
Step 1: Calculate the gauge pressure due to the liquid column
The gauge pressure due to the liquid column can be calculated using the formula:
Pg=ρgh
Where:
- ρ is the density of the liquid (given as 2×103kg/m3).
- g is the acceleration due to gravity (approximately 9.81m/s2).
- h is the depth of the bubble (given as 5cm=0.05m).
Substituting the values:
Pg=(2×103)×(9.81)×(0.05)
Calculating this gives:
Pg=2×103×9.81×0.05=981Pa
Step 2: Calculate the total external pressure Po
The total external pressure Po is the sum of atmospheric pressure and the gauge pressure:
Po=Patm+Pg
Where:
- Patm is the atmospheric pressure (given as 1.01×105Pa).
Substituting the values:
Po=1.01×105+981
Calculating this gives:
Po=1.01×105+981=1.01981×105Pa
Step 3: Calculate the excess pressure inside the bubble
The excess pressure due to surface tension is given by:
Pexcess=2SR
Where:
- S is the surface tension (given as 0.082N/m).
- R is the radius of the bubble (given as 0.2mm=0.2×10−3m).
Substituting the values:
Pexcess=2×0.0820.2×10−3
Calculating this gives:
Pexcess=0.1640.0002=820Pa
Step 4: Calculate the total pressure inside the bubble
Now we can find the total pressure inside the bubble using the formula:
Pi=Po+Pexcess
Substituting the values:
Pi=1.01981×105+820
Calculating this gives:
Pi=1.01981×105+0.00082×105=1.0282×105Pa
Final Answer
Thus, the total pressure inside the spherical air bubble is:
Pi=1.0282×105Pa
---
- Pi is the total pressure inside the bubble.
- Po is the pressure exerted on the bubble from the outside.
- S is the surface tension of the liquid.
- R is the radius of the bubble.
- ρ is the density of the liquid (given as 2×103kg/m3).
- g is the acceleration due to gravity (approximately 9.81m/s2).
- h is the depth of the bubble (given as 5cm=0.05m).
- Patm is the atmospheric pressure (given as 1.01×105Pa).
- S is the surface tension (given as 0.082N/m).
- R is the radius of the bubble (given as 0.2mm=0.2×10−3m).
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - A
50 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - B
23 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J
9 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-D)
14 Videos
Similar Questions
Calculate the pressue inside air bubble of diameter 0.2 mm situated just below the surface of water. Surface tension of water is 72×10−3Nm−1.
View SolutionThe pressure inside an air bubble of radius 2 cm formed 20 cm below an open water surface is (Given surface tension of water = 70×10−3Nm−1)
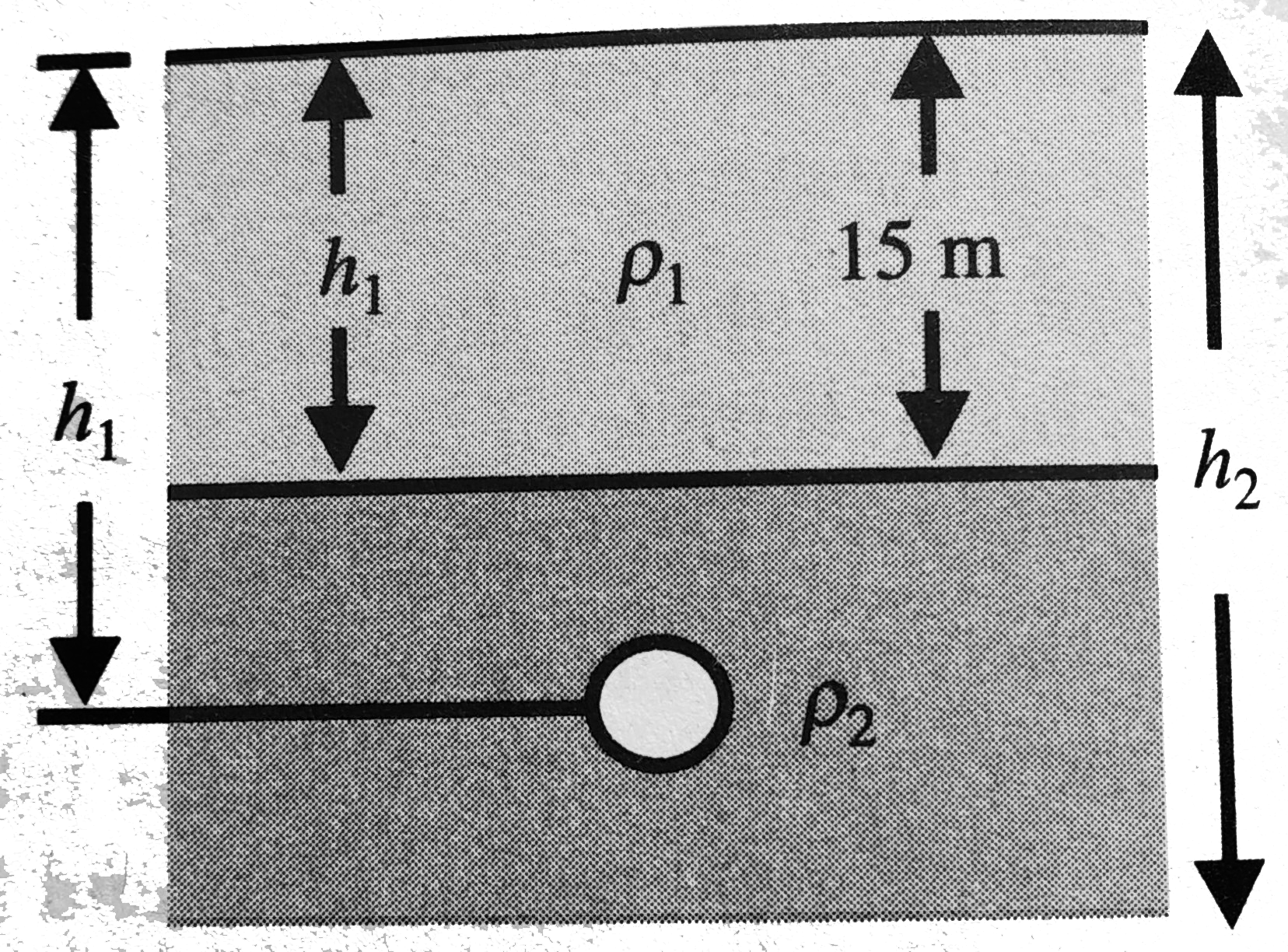
View SolutionCalculate the pressure indise a small air bubble of radius 0.01mm situated at a depth of h=20m below the fre surface of liquid of density ρ1=103kg/m3,ρ2=800km/m3 and surface tension T2=7.5×10−2N/m. The thickness of the first liqid is h1=15m and h2=25m.
View SolutionTo what height does a liquid of density 0.4×103 kg m−3 and surface tension 0.05 Nm−1 rise in a capillary tube of radius 0.2 mm when dipped in ? [Given cosθ=0.4g=10ms−2]
View SolutionFind the pressure inside an air bubble of radius 1 mm at a depth of 20 m in water. (Assume P0 105N/m2, surface tension of water 0.072N/m )
View SolutionThe pressure inside a soap bubble of radius 1 cm balances a 1.5 mm column of oil of density 800 kgm−3. Find the surface tension of the soap solution.
View SolutionWhat should be the pressure inside a small air bubble of 0.1mm radius situated just below the surface of water? Surface tension of water =72×10−3N/m and atmospheric pressure =1.013×105N/m2
View SolutionA spherical air bubble is formed in water at a depth of 1.2 m from the surface. The diameter of the bubble is 0.6 mm and surface tension of water is 0.073Nm−1. Calculate the pressure inside . Atmospheric pressure =10.3m of water.
View SolutionThe absolute pressure at a depth h below the surface of a liquid of density ρ is [Given Pa = atmospheric pressure, g = acceleration due to gravity]
View SolutionWhat should be the pressure inside a small air bubble of 0.1mm radius situated just below the water surface. Surface tension of water =7.2×10−2N/m and atmosphere pressure=1.013×105N/m2.
View Solution
