A rubber ball floats on water with its 1/3 rd volume outside water. What is the density of rubber?
The correct Answer is:
To find the density of rubber when a rubber ball floats on water with one-third of its volume above the surface, we can follow these steps:
1. Identify the Volume of the Ball:
Let the total volume of the rubber ball be V.
2. Determine the Volume Above Water:
Since one-third of the ball's volume is above the water, we can express this as:
Volume above water=13V
3. Calculate the Volume Immersed in Water:
The volume of the ball that is submerged in water can be calculated by subtracting the volume above water from the total volume:
Volume immersed=V−13V=23V
4. Apply Archimedes' Principle:
According to Archimedes' Principle, the weight of the water displaced by the submerged part of the ball is equal to the weight of the ball itself. This can be expressed as:
Weight of water displaced=Weight of the ball
5. Express the Weights:
The weight of the water displaced can be calculated using the density of water (ρwater) and the volume immersed:
Weight of water displaced=ρwater×Volume immersed=ρwater×23V
The weight of the ball can be expressed using the density of rubber (ρrubber):
Weight of the ball=ρrubber×V
6. Set Up the Equation:
Setting the two expressions for weight equal gives us:
ρwater×23V=ρrubber×V
7. Simplify the Equation:
We can cancel V from both sides (assuming V≠0):
ρwater×23=ρrubber
8. Substitute the Density of Water:
The density of water is approximately 1000kg/m3. Substituting this into the equation gives:
ρrubber=1000×23
9. Calculate the Density of Rubber:
Performing the multiplication:
ρrubber=20003≈666.67kg/m3
We can round this to:
ρrubber≈667kg/m3
Final Answer:
The density of rubber is approximately 667kg/m3.
Let the total volume of the rubber ball be V.
Since one-third of the ball's volume is above the water, we can express this as:
Volume above water=13V
The volume of the ball that is submerged in water can be calculated by subtracting the volume above water from the total volume:
Volume immersed=V−13V=23V
According to Archimedes' Principle, the weight of the water displaced by the submerged part of the ball is equal to the weight of the ball itself. This can be expressed as:
Weight of water displaced=Weight of the ball
The weight of the water displaced can be calculated using the density of water (ρwater) and the volume immersed:
Weight of water displaced=ρwater×Volume immersed=ρwater×23V
The weight of the ball can be expressed using the density of rubber (ρrubber):
Weight of the ball=ρrubber×V
Setting the two expressions for weight equal gives us:
ρwater×23V=ρrubber×V
We can cancel V from both sides (assuming V≠0):
ρwater×23=ρrubber
The density of water is approximately 1000kg/m3. Substituting this into the equation gives:
ρrubber=1000×23
Performing the multiplication:
ρrubber=20003≈666.67kg/m3
We can round this to:
ρrubber≈667kg/m3
The density of rubber is approximately 667kg/m3.
Topper's Solved these Questions
- UPTHRUST IN FLUIDS, ARCHIMEDES' PRINCIPLE AND FLOATATIONBook:ICSEChapter:UPTHRUST IN FLUIDS, ARCHIMEDES' PRINCIPLE AND FLOATATIONExercise:EXERCISE 5(c) (Multiple Choice Question)
Explore 3 Videos
- SOUNDBook:ICSEChapter:SOUNDExercise:TOPIC 2 Infrasonic and Ultrasonic Waves ( 3 Marks Questions)
Explore 3 Videos
Similar Questions
A cubical block of side 0.5 M floats on water with 30% of its volume under water. What is the maximum weight that can be put on the block without fully submerging it under water?
[Take density of water =103kg/m3]
View SolutionA body floats in water with 40% of its volume outside water. When the same body floats in an oil. 60% of its volume remians outside oil. The relative density of oil is
View SolutionA block of wood floats on water with 25 th of its volume above the water surface. Calculate the density of wood.
View SolutionA wooden block floats in water with two third of its volume submerged. A. Calculate the density of wood.b. When the same block is placed in oil, three - quarter of its volume in immersed in oil. Calculate the density of oil.
View SolutionAn ice cube floats in water. What percentage of volume is outside water. Density of water =1g/cc, density of ice =0.9g/cc.
View Solution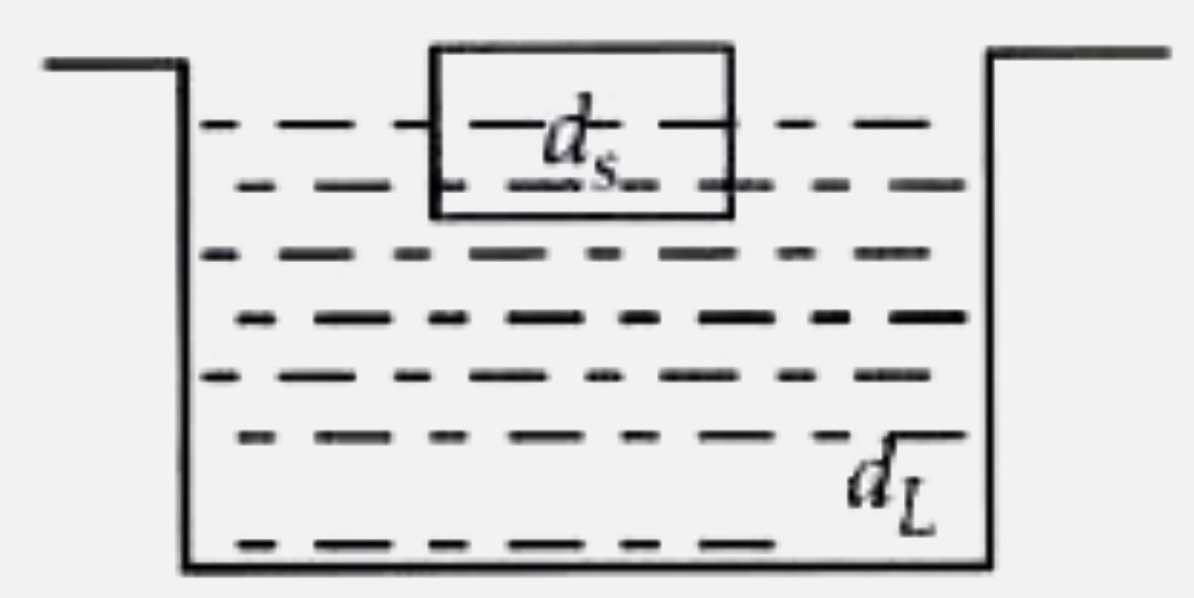
The figure above shows a solid of density dS floating in a liquid of density dL.
The same solid floats in water with 3th5 of its volume immersed in it. Calculate the density of the solid. (density of water = 1 g cm−3 )
View Solution(a) Ice floats in water with about wine-tenths of its volume submerged. What is the fraction sub merged for an iceberg floating on freshwater lake of a hypothetical) planet whose gravity is to times that of the earth?
(b) What is the fractional volume submerged of an ice cube in a fall of water placed in an enclosure which is freely falling under gravity?
View SolutionA block of wood of volume 25cm3 floats on water with 20cm3 of its volume immersed. Calculate (i) the density, and (ii) the weight of block of wood.
View SolutionA wooden block floating in a bucket of water has 4/5 of its volume submerged. When certain amount of an oil is poured into the bucket, it is found that the block is just under the oil surface with half of its volume under water and half in oil. The density of oil relative to that of water is
View SolutionA solid of density 2.5 kg m−3 floats in a fluid with one-third of its volume immersed in it. What is the density of the fluid?
View Solution

