A column of water 40cm high supports a 30cm column of an unknown liquid . What is the density of the liquid ?
To find the density of the unknown liquid supported by a column of water, we can use the principle that the pressure at the base of both columns is equal. Here’s a step-by-step solution:
Step 1: Understand the relationship between pressure and height of the liquid columns
The pressure exerted by a column of liquid is given by the formula:
P=ρ⋅g⋅h
where:
- P is the pressure,
- ρ is the density of the liquid,
- g is the acceleration due to gravity (which we can assume to be constant and will cancel out),
- h is the height of the liquid column.
Step 2: Set up the equation for both columns
For the water column and the unknown liquid column, we can set up the equation:
ρwater⋅g⋅hwater=ρliquid⋅g⋅hliquid
Step 3: Cancel out g from both sides
Since g is present in both terms, we can cancel it out:
ρwater⋅hwater=ρliquid⋅hliquid
Step 4: Rearrange the equation to solve for the density of the unknown liquid
Rearranging gives us:
ρliquid=ρwater⋅hwaterhliquid
Step 5: Substitute the known values
We know:
- The density of water, ρwater=1000kg/m3 (or 103kg/m3),
- The height of the water column, hwater=40cm=0.4m,
- The height of the unknown liquid column, hliquid=30cm=0.3m.
Substituting these values into the equation:
ρliquid=1000kg/m3⋅0.4m0.3m
Step 6: Calculate the density of the unknown liquid
Calculating this gives:
ρliquid=4000.3kg/m3=40003kg/m3≈1333.33kg/m3
Thus, the density of the unknown liquid is approximately:
ρliquid≈1.33×103kg/m3
Final Answer:
The density of the unknown liquid is approximately 1333.33kg/m3.
---
The pressure exerted by a column of liquid is given by the formula:
P=ρ⋅g⋅h
where:
- P is the pressure,
- ρ is the density of the liquid,
- g is the acceleration due to gravity (which we can assume to be constant and will cancel out),
- h is the height of the liquid column.
For the water column and the unknown liquid column, we can set up the equation:
ρwater⋅g⋅hwater=ρliquid⋅g⋅hliquid
Since g is present in both terms, we can cancel it out:
ρwater⋅hwater=ρliquid⋅hliquid
Rearranging gives us:
ρliquid=ρwater⋅hwaterhliquid
We know:
- The density of water, ρwater=1000kg/m3 (or 103kg/m3),
- The height of the water column, hwater=40cm=0.4m,
- The height of the unknown liquid column, hliquid=30cm=0.3m.
ρliquid=1000kg/m3⋅0.4m0.3m
Calculating this gives:
ρliquid=4000.3kg/m3=40003kg/m3≈1333.33kg/m3
ρliquid≈1.33×103kg/m3
The density of the unknown liquid is approximately 1333.33kg/m3.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - A
50 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - B
23 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J
9 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-D)
14 Videos
Similar Questions
Two miscible liquids of densities 1.2gm/cm and 1.4gm/cm aer mixed with a proportion ratio of their volumes equal to 2.5: what is the density of redulting liquid?
View SolutionA metallic sphere weighs 210g in air, 180 g in water and 120 g in an unknown liquid. Find the density of metal and of liquid.
View SolutionHow many molecule are present in 12 L of liquid CCl4? The density of the liquid is 1.59 g cm−3?
View SolutionA piece of steel has a weight w in air, w1 when completely immersed in water and w2 when completely immersed in an unknown liquid. The relative density (specific gravity) of liquid is
View SolutionA piece of steel has a weight w in air, w1 when completely immersed in water and w2 when completely immersed in an unknown liquid. The relative density (specific gravity) of liquid is
View SolutionAn air bubble of diameter 2 cm is allowed to rise through a long cylindrical column of viscous liquid and travels at the rate of 0.21cms−1. If the density of the liquid is 1.47gcm−3. find the coefficient of viscosity. Density of air is neglected.
View SolutionA 0.02 cm liquid column balances the excess pressure inside a soap bubble of radius 7.5 mm. Determine the density of the liquid. Surface tension of soap solution 0.03Nm−1.
View SolutionAn open -ended U-tube of uniform cross-sectional area contains water (density 1.0g/cm23) standing initially 20 cm from the bottom in each arm. An immiscible liquid of density 4.0g/cm2 is added to one arm until a layer 5 cm high forms, as shown in the figure above. What is the ratio h2/h1 of the heights of the liquid in the two arms ?
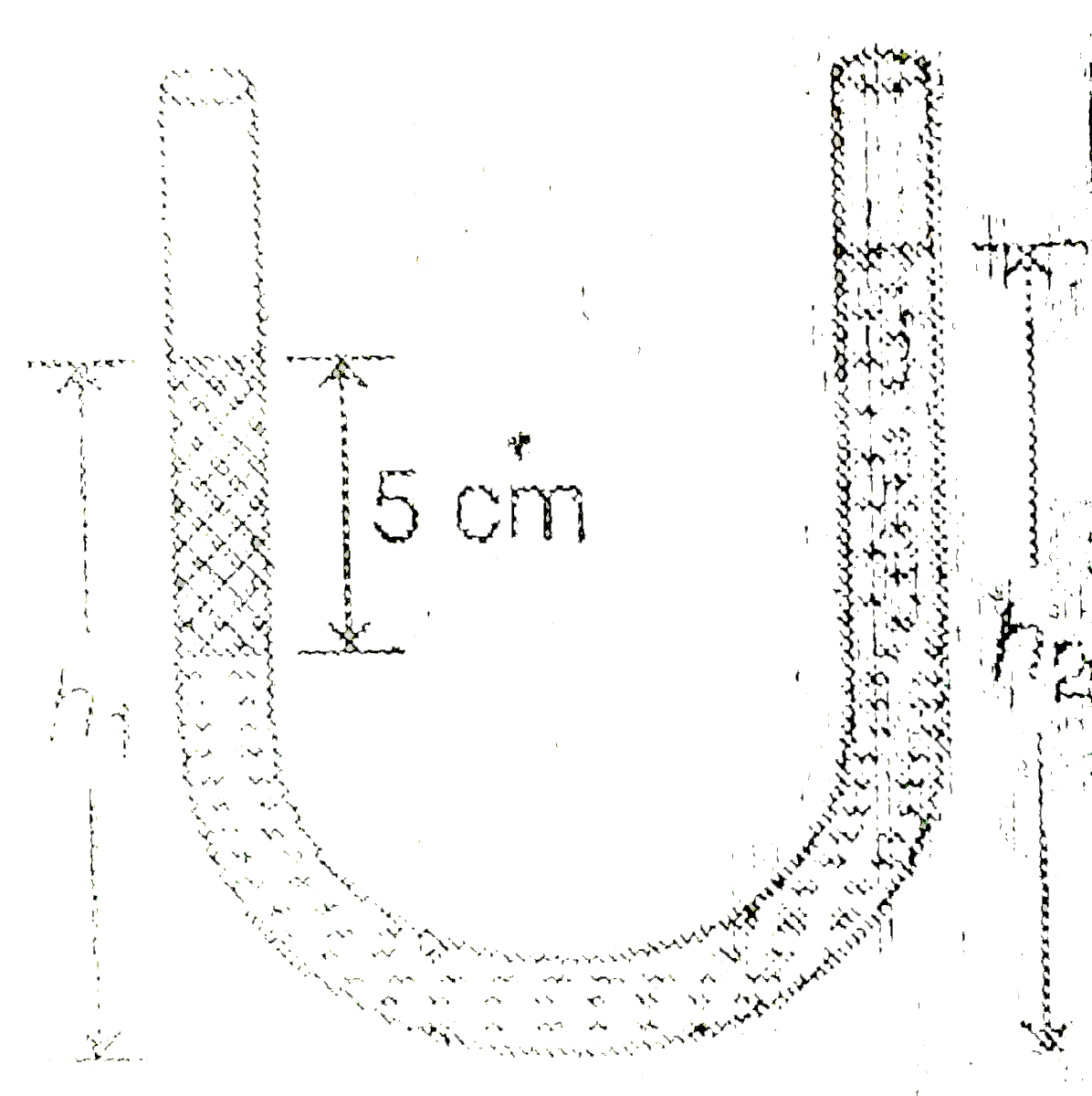
View SolutionColumn - I and Column - II contains four emtries each. Entries of Column -I are to be matched with some entries of Column - II . One or more than one entries of Column -I may have the matching with the same entries of Column - II.
column-Icolumn-II(A) Chemisorption(P) Not specific and decreases with temperature (B) physisorption(Q)sepecific and increases with temperature(C) Desorption of a solute on liquid surface(R) Increases the surface tension of the liquid (D)Adsorption of a solute on a liquid (S) Decreases the surface tension of the liquid
View SolutionA block of material has a density ρ1 and floats three-fourth submerged in a liquid of unknown density. Show tht the density ρ2 of the unknown liquid is given by ρ2=43ρ1.
View Solution
