A cubical block of side 'a' is held at rest, against a rough vertical wall by applying a force acting along the centre. The mass of the block is . Taking acceleration due to gravity as 'g' , determine
The minimum coefficient of friction between the block and wall
The torque by normal reaction about the centre of mass
To solve the problem, we will break it down into two parts as requested.
Part (i): Minimum Coefficient of Friction
1. Identify the forces acting on the block:
- The gravitational force Fg=mg acting downward.
- The applied force F acting horizontally towards the wall.
- The normal force N acting perpendicular to the wall.
- The frictional force f acting upward to prevent the block from sliding down.
2. Establish equilibrium conditions:
- Since the block is at rest, the net force in both horizontal and vertical directions must be zero.
- In the horizontal direction:
N=F
- In the vertical direction:
f=mg
3. Relate frictional force to the normal force:
- The maximum static frictional force is given by:
fmax=μN
- For equilibrium, we have:
mg=μN
4. Substitute the normal force:
- From the horizontal equilibrium, substitute N=F into the friction equation:
mg=μF
5. Solve for the minimum coefficient of friction:
- Rearranging gives:
μ=mgF
Part (ii): Torque by Normal Reaction about the Centre of Mass
1. Identify the point of application of forces:
- The normal force N acts at the wall, which is at the edge of the block.
- The friction force f acts at the bottom of the block.
2. Calculate the torque due to the normal force:
- The torque τ about the center of mass due to the normal force is given by:
τN=N⋅dN
- Here, dN is the perpendicular distance from the center of mass to the line of action of the normal force. Since the block is cubical with side a, this distance is a2.
3. Substitute the normal force:
- We know N=F, so:
τN=F⋅a2
4. Calculate the torque due to friction:
- The torque due to friction τf is similarly calculated:
τf=f⋅df
- The distance df from the center of mass to the line of action of the friction force is also a2, so:
τf=mg⋅a2
5. Equate torques:
- In equilibrium, the torque due to the normal force balances the torque due to friction:
τN=τf
Final Answers
- (i) The minimum coefficient of friction μ is given by:
μ=mgF
- (ii) The torque by the normal reaction about the center of mass is:
τN=F⋅a2
- The gravitational force Fg=mg acting downward.
- The applied force F acting horizontally towards the wall.
- The normal force N acting perpendicular to the wall.
- The frictional force f acting upward to prevent the block from sliding down.
- Since the block is at rest, the net force in both horizontal and vertical directions must be zero.
- In the horizontal direction:
N=F
- In the vertical direction:
f=mg
- The maximum static frictional force is given by:
fmax=μN
- For equilibrium, we have:
mg=μN
- From the horizontal equilibrium, substitute N=F into the friction equation:
mg=μF
- Rearranging gives:
μ=mgF
- The normal force N acts at the wall, which is at the edge of the block.
- The friction force f acts at the bottom of the block.
- The torque τ about the center of mass due to the normal force is given by:
τN=N⋅dN
- Here, dN is the perpendicular distance from the center of mass to the line of action of the normal force. Since the block is cubical with side a, this distance is a2.
- We know N=F, so:
τN=F⋅a2
- The torque due to friction τf is similarly calculated:
τf=f⋅df
- The distance df from the center of mass to the line of action of the friction force is also a2, so:
τf=mg⋅a2
- In equilibrium, the torque due to the normal force balances the torque due to friction:
τN=τf
- (i) The minimum coefficient of friction μ is given by:
μ=mgF
- (ii) The torque by the normal reaction about the center of mass is:
τN=F⋅a2
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration
4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)
62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
A block of mass 1 kg is held at rest against a rough vertical surface by pushing by a force F horizontally. The coefficient of friction is 0.5. When

View SolutionA block weighs W is held against a vertical wall by applying a horizontal force F. The minimum value of F needed to hold the block is
View Solution
Knowledge Check
A block of mass M is held against a rough vertical wall by pressing it with a finger . If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g , calculate the minimum force required to be applied by the finger to hold the block against the wall.
AμMgBMgCMgμD2μMg
Block a of mass 4 kg is to be kept at rest against a smooth vertical wall by applying a force F as shown in figure. The force required is :- (g=10m/s2)
View SolutionA block of mass M is held against a rough vertical wall by pressing it with a finger . If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g , calculate the minimum force required to be applied by the finger to hold the block against the wall.
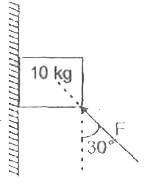
View SolutionA block of mass 10 kg is held at rest against a rough vertical wall [μ=0.5] under the action a force F as shown in figure. The minimum value of F required for it is (g=10m/s2)
View SolutionA block of mass 1 kg is pushed against a rough vertical wall of μ=0.1
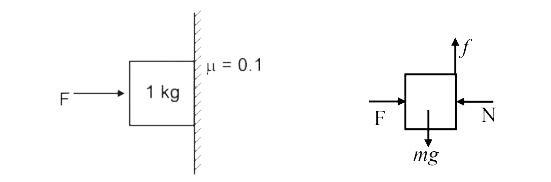
For F = 150, 50 or 100 N the force of friction on the blocks is respectively :
View SolutionA block of mass 0.1 kg is held against a wall applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is :
View SolutionA block of mass 0.1 is held against a wall applying a horizontal force of 5N on block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is:
View SolutionA body is pushed against vertical wall as shown. If the coefficient of friction between the body and the wall is 0.5, the magnitude of acceleration of the block is 10 K. Where K is
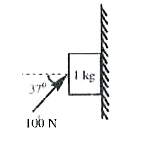
View Solution
