A particle moves in x-y plane under action of a path dependent force F=yˆi+xˆj. The work done by the force as it moves in x-y plane can be evaluated by solving the integral ∫→F.→dr,where →dr=dxˆi+dyˆj. The position coordinates x and y will vary according to some constraint determined by teh path followed by the particle. For example, if particle moves along a straight line from one position to other, then an possible rarticle. For example, if particle moves along a straight line from one position to other, then a possible relation is y=mx+c. NOw. try to solve the following questions.
1. The particel moves along a straight line from origin to (a ,a) . The work done by the force on the particle is
(1)a2 (2)2s (3)a22 (4)Zero
2. The particle moves from (0,0) to (a,0) and then from, (a,0) to (a,a), in straight line paths. The work done by the force on the particle is
(1)a2 (2)2a (3)a22 (4) Zero
3. The differential work by the given force over an elementary displacement is given as dW=→F.→dr=ydx+xdy
This can be expressed as dW=d(xy). From this, it can be inferred that the work done by the force
(1) Depends only on initial and final values of x and y
(2) Depends on initial and final values and on the path followed
(3) Is zero for any values of x and y
(4) Is zero when object returns to original position after following any path
To solve the given questions step by step, we will analyze each part of the problem systematically.
Question 1:
The particle moves along a straight line from origin to (a, a). The work done by the force on the particle is:
1. Identify the path: The particle moves from (0, 0) to (a, a). The equation of the line is y=x.
2. Express dy in terms of dx: Since y=x, we have dy=dx.
3. Write the differential displacement vector:
→dr=dx^i+dy^j=dx^i+dx^j=dx(^i+^j).
4. Substitute y in the force vector: The force vector is given by →F=y^i+x^j. Since y=x, we can write:
→F=x^i+x^j=x(^i+^j).
5. Calculate the dot product →F⋅→dr:
→F⋅→dr=x(^i+^j)⋅dx(^i+^j)=xdx(^i⋅^i+^j⋅^j)=xdx(1+1)=2xdx.
6. Integrate to find the work done:
W=∫a02xdx=2(x22)a0=2(a22−0)=a2.
Final Answer for Question 1: (1)a2
Question 2:
The particle moves from (0, 0) to (a, 0) and then from (a, 0) to (a, a). The work done by the force on the particle is:
1. Path 1: From (0, 0) to (a, 0):
- Here, y=0 and dy=0.
- The displacement vector is →dr=dx^i.
- The force becomes →F=0^i+x^j=x^j.
- Therefore, →F⋅→dr=0.
- Work done W1=∫a00dx=0.
2. Path 2: From (a, 0) to (a, a):
- Here, x=a (constant) and dx=0.
- The displacement vector is →dr=dy^j.
- The force becomes →F=y^i+a^j.
- Therefore, →F⋅→dr=ady.
- Work done W2=∫a0ady=a(y)a0=a2.
3. Total work done:
W=W1+W2=0+a2=a2.
Final Answer for Question 2: (1)a2
Question 3:
The differential work by the given force over an elementary displacement is given as dW=→F⋅→dr=ydx+xdy. This can be expressed as dW=d(xy). From this, it can be inferred that the work done by the force:
1. Understanding the expression: The expression dW=d(xy) implies that the work done depends on the change in the product xy.
2. Path independence: Since dW can be expressed as a total differential, the work done only depends on the initial and final values of x and y, not on the path taken.
3. Conclusion: The work done depends only on the initial and final values of x and y.
Final Answer for Question 3: (1)Depends only on initial and final values of x and y
The particle moves along a straight line from origin to (a, a). The work done by the force on the particle is:
→dr=dx^i+dy^j=dx^i+dx^j=dx(^i+^j).
→F=x^i+x^j=x(^i+^j).
→F⋅→dr=x(^i+^j)⋅dx(^i+^j)=xdx(^i⋅^i+^j⋅^j)=xdx(1+1)=2xdx.
W=∫a02xdx=2(x22)a0=2(a22−0)=a2.
The particle moves from (0, 0) to (a, 0) and then from (a, 0) to (a, a). The work done by the force on the particle is:
- Here, y=0 and dy=0.
- The displacement vector is →dr=dx^i.
- The force becomes →F=0^i+x^j=x^j.
- Therefore, →F⋅→dr=0.
- Work done W1=∫a00dx=0.
- Here, x=a (constant) and dx=0.
- The displacement vector is →dr=dy^j.
- The force becomes →F=y^i+a^j.
- Therefore, →F⋅→dr=ady.
- Work done W2=∫a0ady=a(y)a0=a2.
W=W1+W2=0+a2=a2.
The differential work by the given force over an elementary displacement is given as dW=→F⋅→dr=ydx+xdy. This can be expressed as dW=d(xy). From this, it can be inferred that the work done by the force:
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - IILUSTRATION
2 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - TRY YOURSELF
95 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
Knowledge Check
A force F is related to the position of a particle by the relation F=(10x2)N . Find the work done by the force when the particle moves from x=2m→x=4m.
A563 JB560 JC5603 JD3560 J
The force F acting on a particle is moving in a straight line as shown in figure. What is the work done by the force on the particle in the 4 m of the trajectory?
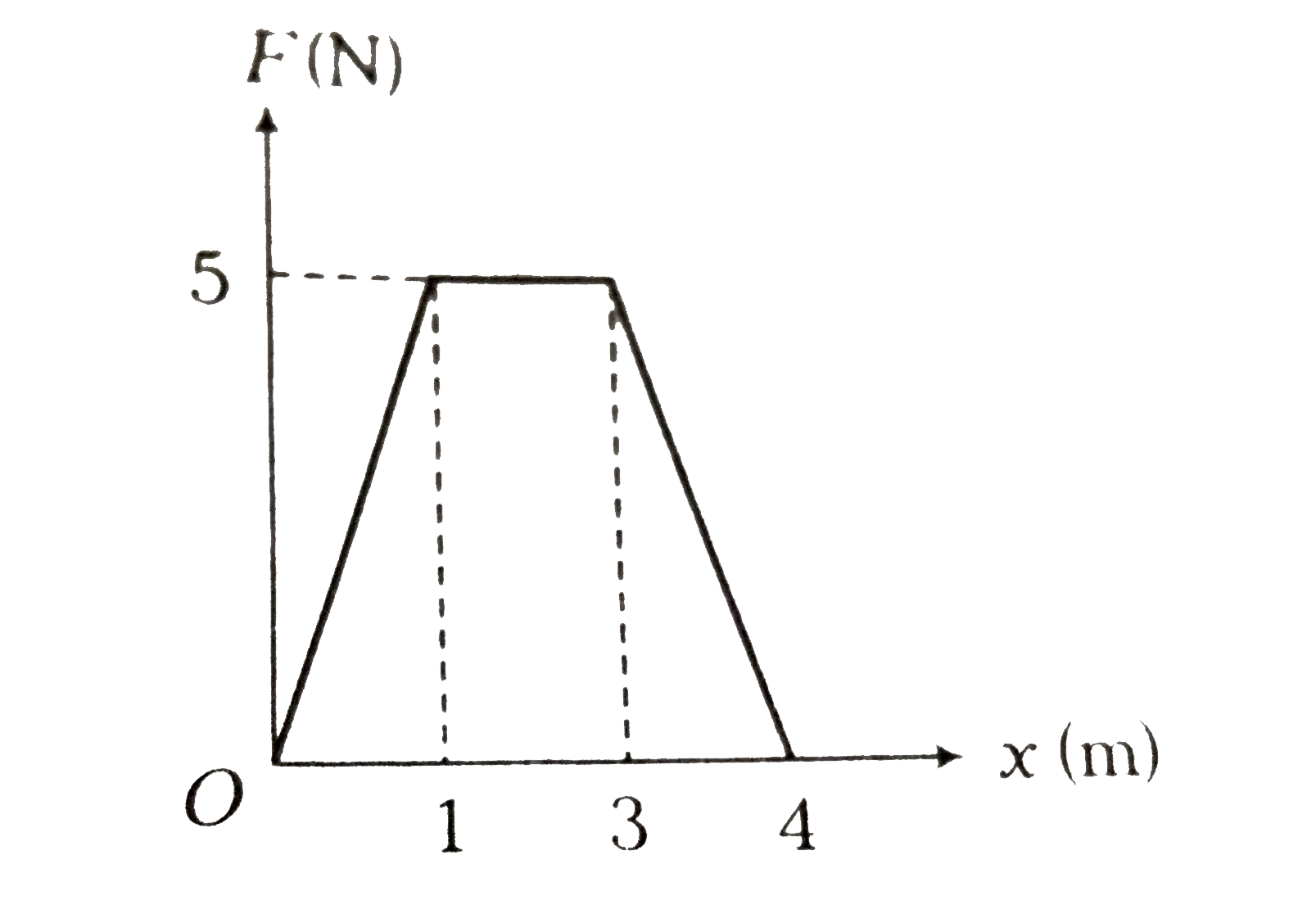
View SolutionA particle moves along the x-axis from x=0 to x=5m under the influence of a given by F=7−2x+3x2. The work done by the applied force to the particle is.
View SolutionA force f=10+2x acts on a particle moving in straight line on x axis the work done by this force during a displacement from x=0 and x=3m
View SolutionA particle moves in the x-y plane. It x and y coordinates vary with time t according to equations x=t2+2t and y=2t. Possible shape of path followed by the particle is
View SolutionA particle is moving with a constant speed along a straight line path. A force is not required to
View SolutionA force F=−k(^ˆi+xˆj) (where k is a positive constant) acts on a particle moving in the x−y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0) and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
(a) −2ka2 , (b) 2ka2,(c)-ka^(2),(d)ka^(2)
View SolutionForce F on a particle moving in a straight line varies with distance d as shown in the figure. The work done on the particle during its displacement of 12m is
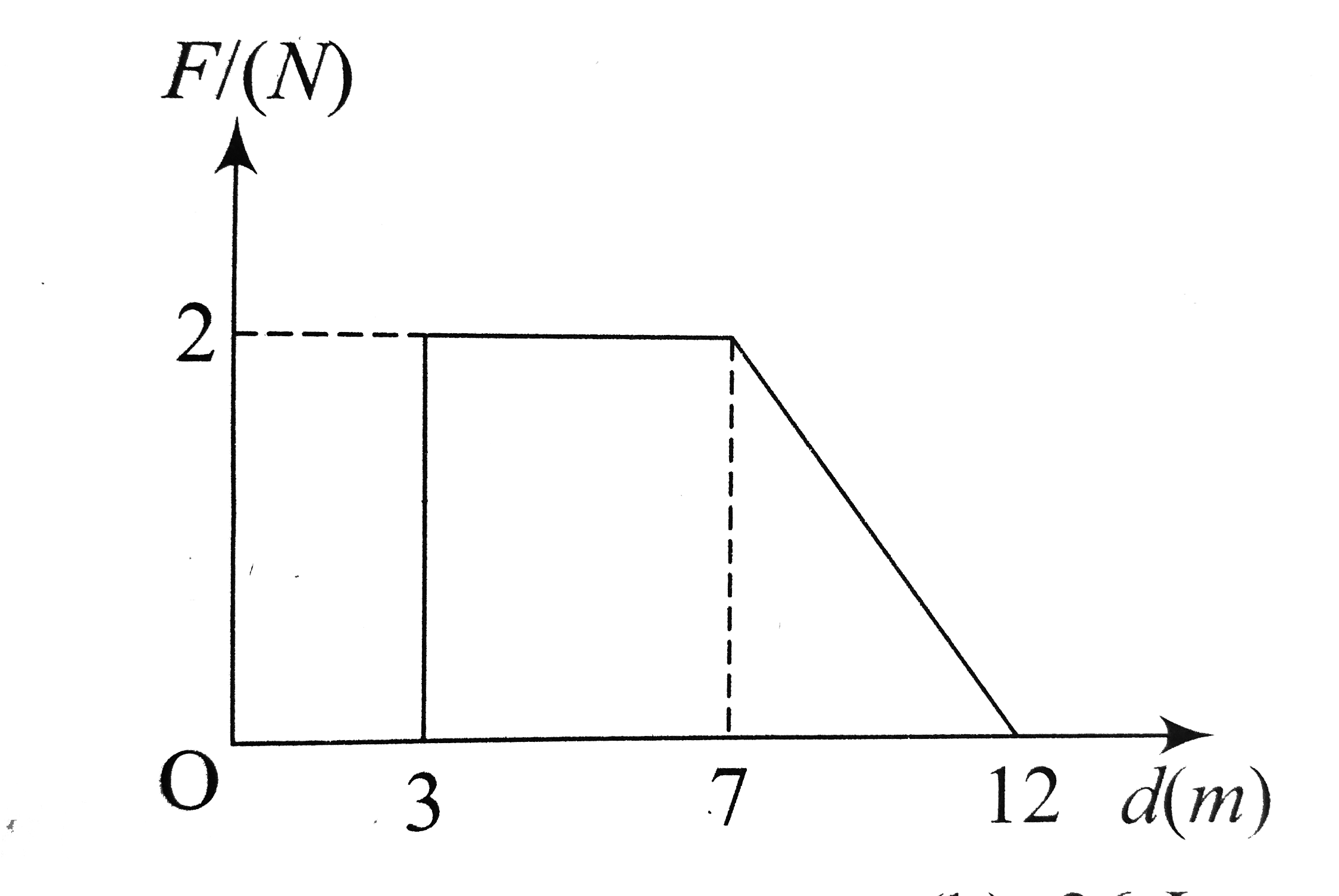
View Solution
