Question

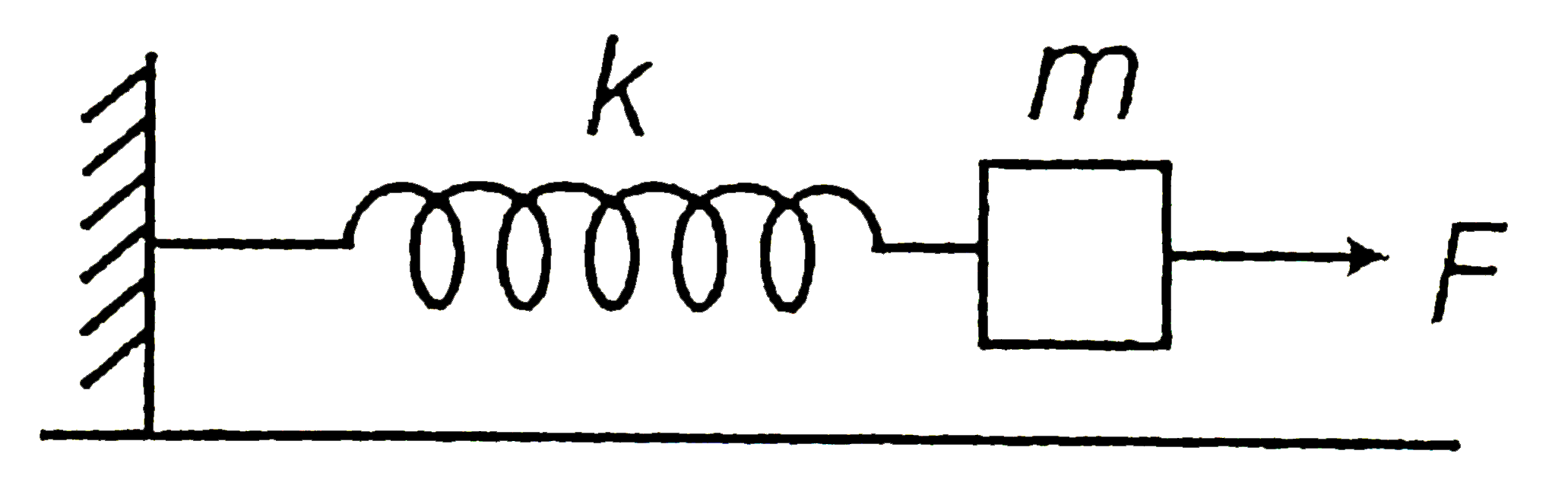
Figure shows a block of mass 'm' resting on a smooth horizontal surface. It is connected to a rigid wall by a massless spring of stiffness 'k'. The spring is in its natural length. A constant horizontal force F starts acting on the block towards right. Find (i) speed of the block as it moves throught a distance x, (ii) speed when the block is in equlibrium and (iii) maximum extension produced in the speing.

Explanation

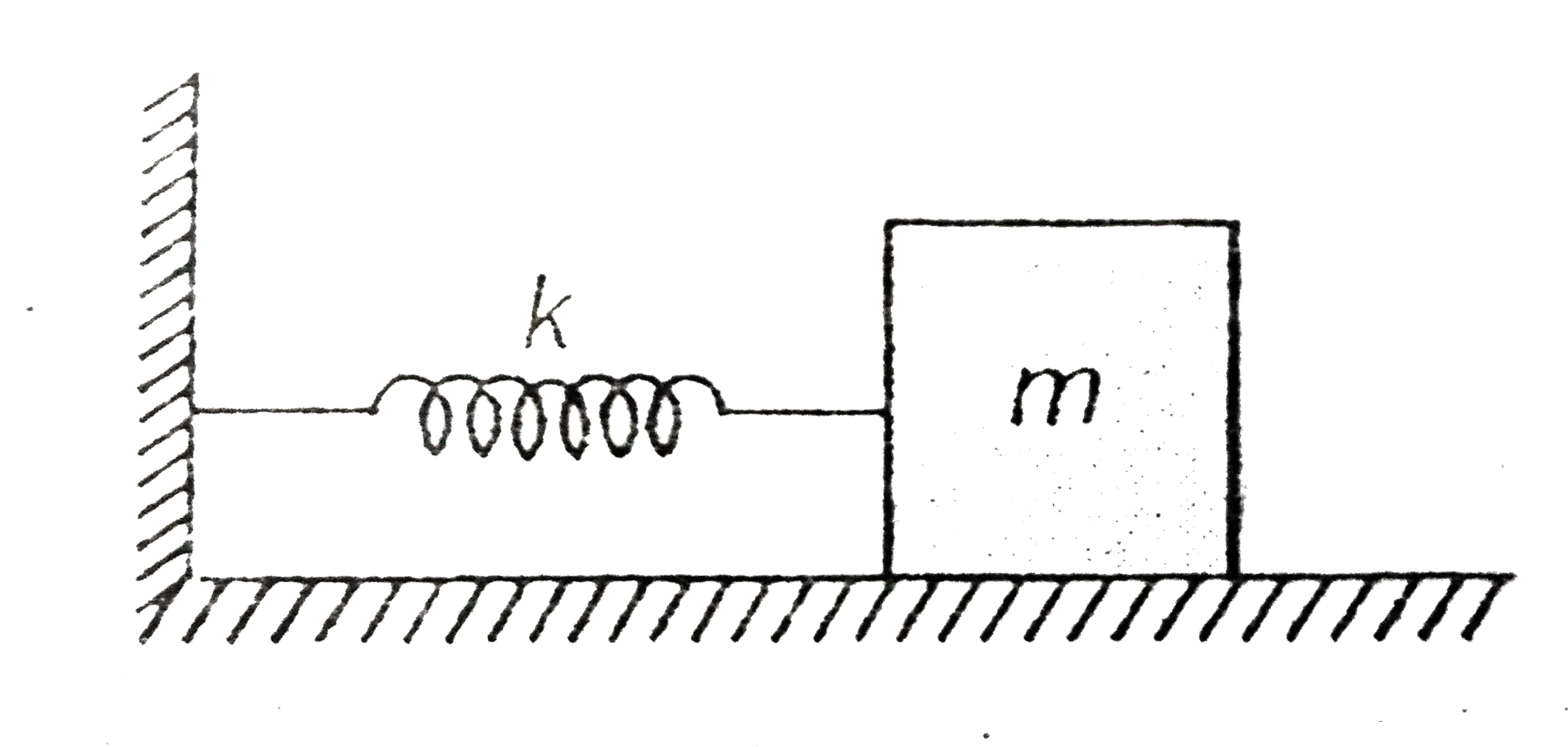
The various forces action on the block during its motion are (a) Weight, mg, downwards (b) Normal reaction N upwards (c ) Spring force, kx, leftward. The work done by the weight and normal reaction is zero
The work done by the speing force is `W_(sp)=-underset(0)overset(x)intkxdx`

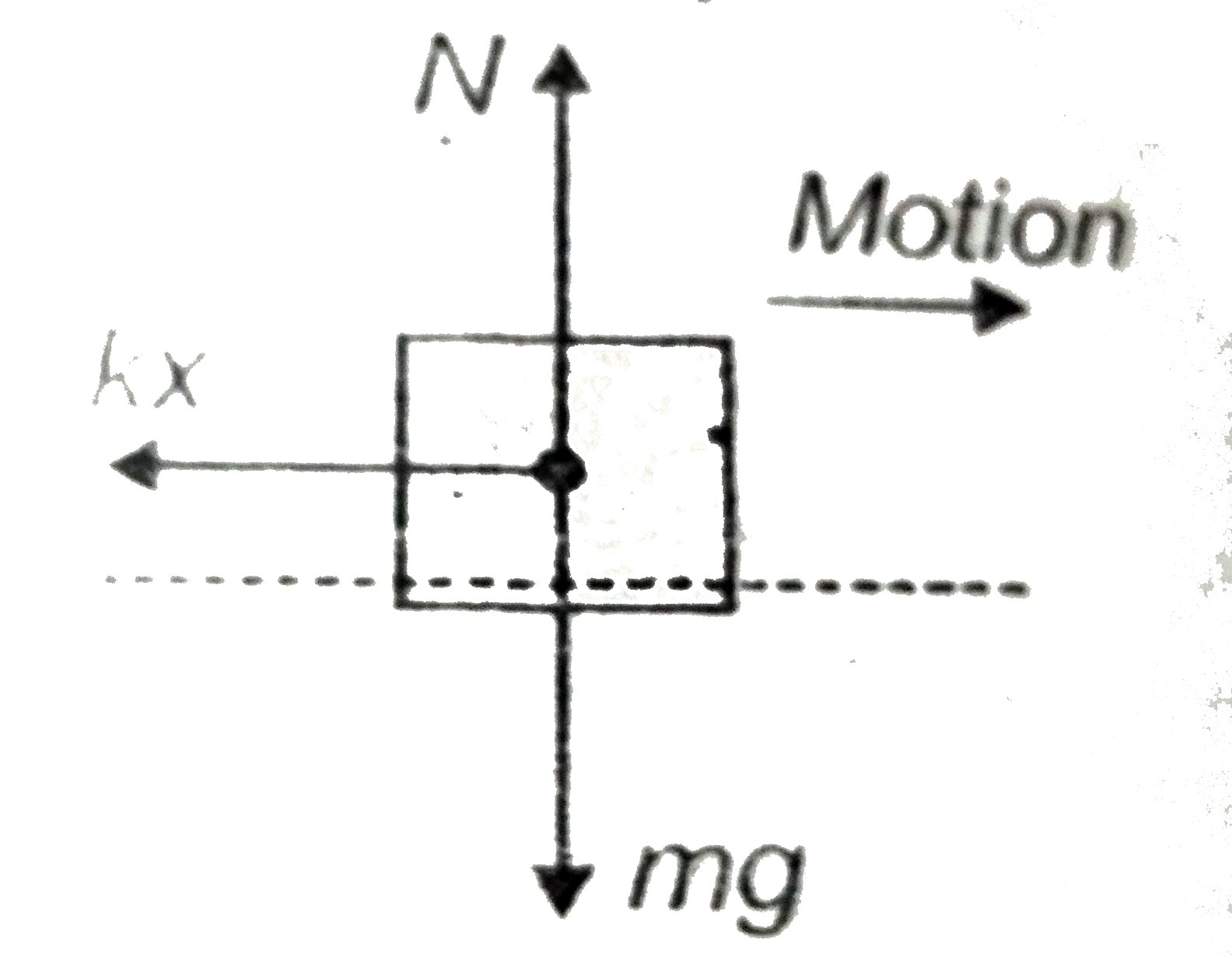
negative sign appears as block moves towards right, whereas force act feftward.
(i) By work-energy principle, `W=Deltak`
`implies-underset(0)overset(x)intkxdx=1/2mv_(1)^(2)-1/2mv^(2)`
`implies(mv_(1)^(2)-mv^(2))/(2)=(-kx^(2))/(2)`
`thereforev_(1)=sqrt(v^(2)-k/mx^(2))`
(ii) The compression in the spring increases till the block moves towards teh wall. At the instant speed of the block reduces to zero, the compression is maximum. After that, compression will start decresing again.
So when `x=x_(max)v_(f)=0`
`implies0=sqrt(v^(2)-k/mx_(max)^(2))`
`or x_(max)=sqrt((mv^(2))/(k))`