The relation between the acceleration and time for an object is given below. Calculate the velocity with which the object is moving at t = 1 s.
a=3t−4t2
The correct Answer is:0.16m/s.
To solve the problem, we need to find the velocity of the object at t=1 second given the acceleration function a(t)=3t−4t2.
1. Understand the relationship between acceleration and velocity:
The acceleration a is defined as the rate of change of velocity v with respect to time t:
a=dvdt
2. Substitute the given acceleration function:
We can substitute the given acceleration function into the equation:
dvdt=3t−4t2
3. Rearrange the equation for integration:
Rearranging gives us:
dv=(3t−4t2)dt
4. Integrate both sides:
Now, we integrate both sides. The left side integrates to v, and the right side needs to be integrated with respect to t:
∫dv=∫(3t−4t2)dt
5. Perform the integration:
The integral of the left side is:
v=∫(3t−4t2)dt=32t2−43t3+C
where C is the constant of integration.
6. Evaluate the integral at t=1 second:
We need to find the velocity at t=1 second. We substitute t=1 into the integrated equation:
v(1)=32(12)−43(13)+C
This simplifies to:
v(1)=32−43+C
7. Find a value for the constant C:
Since we don't have initial conditions provided (like initial velocity), we can assume C=0 for simplicity. Thus:
v(1)=32−43
8. Calculate the final value:
To combine the fractions, we find a common denominator (which is 6):
v(1)=96−86=16
9. Convert to decimal:
The final velocity at t=1 second is:
v(1)=0.1667 m/s(approximately)
Final Answer:
The velocity of the object at t=1 second is approximately 0.1667m/s.
The acceleration a is defined as the rate of change of velocity v with respect to time t:
a=dvdt
We can substitute the given acceleration function into the equation:
dvdt=3t−4t2
Rearranging gives us:
dv=(3t−4t2)dt
Now, we integrate both sides. The left side integrates to v, and the right side needs to be integrated with respect to t:
∫dv=∫(3t−4t2)dt
The integral of the left side is:
v=∫(3t−4t2)dt=32t2−43t3+C
where C is the constant of integration.
We need to find the velocity at t=1 second. We substitute t=1 into the integrated equation:
v(1)=32(12)−43(13)+C
This simplifies to:
v(1)=32−43+C
Since we don't have initial conditions provided (like initial velocity), we can assume C=0 for simplicity. Thus:
v(1)=32−43
To combine the fractions, we find a common denominator (which is 6):
v(1)=96−86=16
The final velocity at t=1 second is:
v(1)=0.1667 m/s(approximately)
The velocity of the object at t=1 second is approximately 0.1667m/s.
Topper's Solved these Questions
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - A)
50 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - B)
19 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)
2 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
Similar Questions
The position-time (x-t) graph of an object in uniform motion is shown below. Calculate the velocity with which the object is moving.
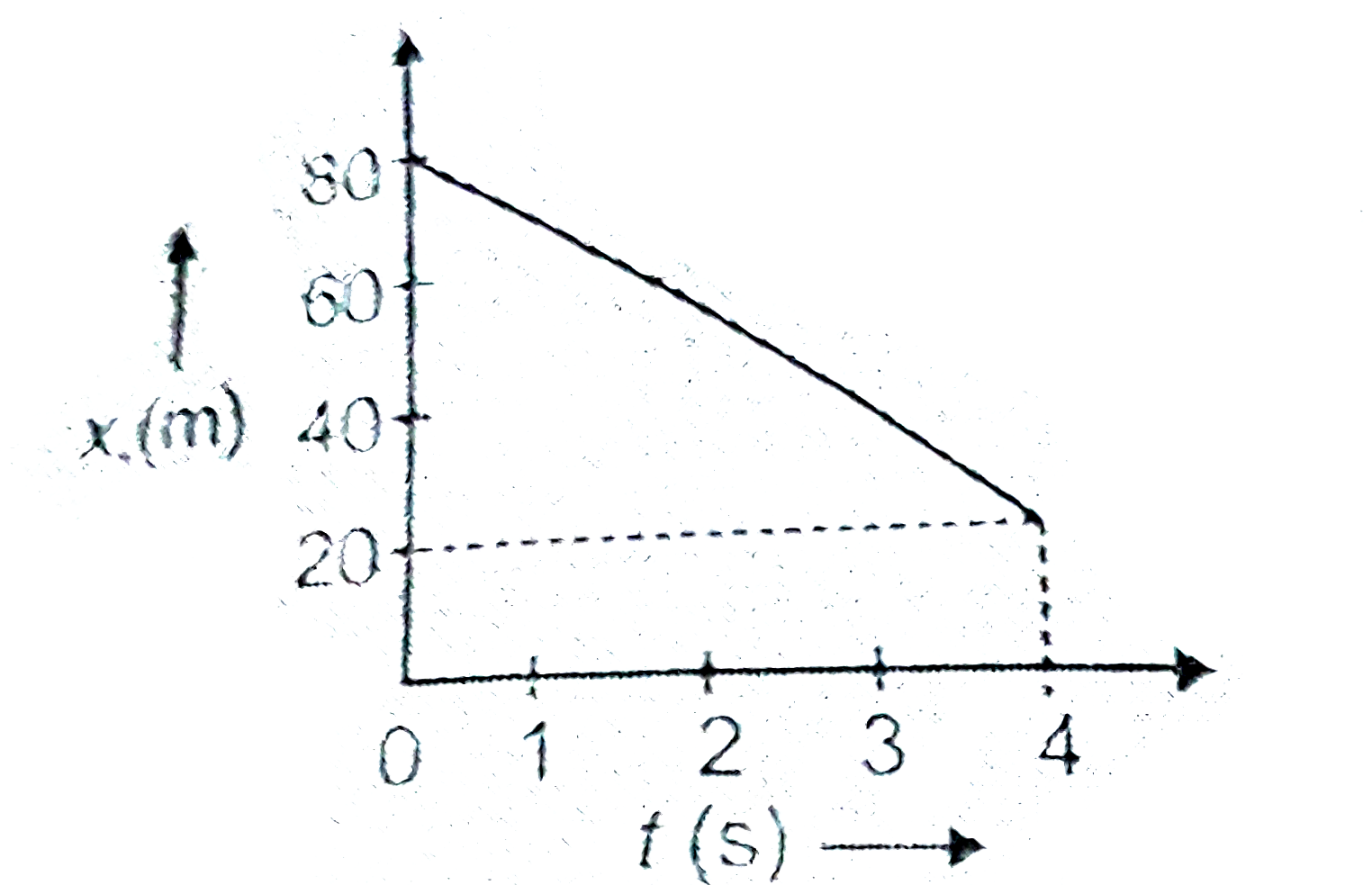
View SolutionIf the relation between acceleration and time for an object is given by
a=2t+4t2
Calculate the position of object from the origin at t = 4 s. Assume the object to be at rest at t=0.
View SolutionThe velocity-time graph of an object is given below. Calculate the average acceleration of the object in the time interval of 4 s to 6 s.

View SolutionIf acceleration of a particle at any time is given by a=2t+5
Calculate the velocity after 5 s, if it starts from rest
View SolutionThe position - time (x−t) graph of an object in uniform motion is shown below, the velocity of object is
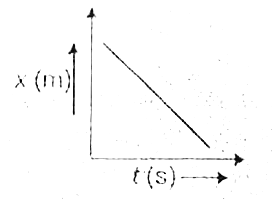
View SolutionThe displacement x of an object is given as a function of time x=2t+3t2
Calculate the instantaneous velocity of the object at t = 2 s
View SolutionThe v-t plot of a moving object ios shown in the figure. The average velocity of the object during the first 10 s is

View SolutionThe velocity of an object is changing with time and relation is given by the following equation.
v=2t+3t2
Calculate the position of the object from the origin at t = 2 s.
Assume particle to be at origin at t = 0
View SolutionThe displacement x of an object is given as a funstion of time, x=2t+3t2. The instantaneous velocity of the object at t = 2 s is
View SolutionVelocity is given by v=4t(1−2t), then find time at which velocity is maximum
View Solution
