Question

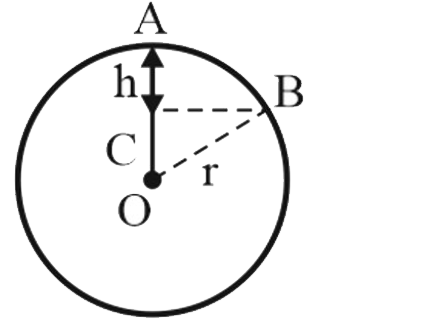
A particle originally at rest at the highest point of a smooth vertical circle is slightly displaced. It will leave the circle at a vertical distance $h$ below the highest points, such that $h$ is equal to

Options

A. `R`
B. `(R)/(4)`
C. `(R)/(2)`
D. `(R)/(3)`

Explanation

To solve the problem, we need to find the vertical distance $$h$$ below the highest point of a smooth vertical circle at which a particle, originally at rest, will leave the circle after being slightly displaced.

1. Understanding the Setup:
- The particle is initially at the highest point of a vertical circle of radius \( r \).
- When slightly displaced, it will start moving downwards due to gravity.

2. Identify Key Points:
- Let the particle be at the highest point initially (point A).
- After being displaced, it moves to a point B at a vertical distance \( h \) below point A.

3. Using Energy Conservation:
- Initially, the particle has potential energy and no kinetic energy since it is at rest.
- At the height \( h \), the potential energy will be converted into kinetic energy.
- The initial potential energy at the highest point is \( mg \cdot r \) (where \( m \) is the mass of the particle and \( g \) is the acceleration due to gravity).
- The potential energy at point B is \( mg(r - h) \).
- The kinetic energy at point B is given by \( \frac{1}{2} mv^2 \).

By conservation of energy:
\( mg \cdot r = mg(r - h) + \frac{1}{2} mv^2 \)

4. Simplifying the Energy Equation:
- Cancel \( m \) from all terms (assuming \( m \neq 0 \)):
\( g \cdot r = g(r - h) + \frac{1}{2} v^2 \)
- Rearranging gives:
\( g \cdot r - g(r - h) = \frac{1}{2} v^2 \)
- This simplifies to:
\( gh = \frac{1}{2} v^2 \quad \text{(Equation 1)} \)

5. Finding the Velocity:
- At the point where the particle leaves the circle, the centripetal force is provided by the component of gravitational force acting towards the center of the circle.
- The centripetal force required for circular motion is \( \frac{mv^2}{r} \).
- The component of weight acting towards the center is \( mg \cos \theta \).
- At the point of leaving the circle, the normal force becomes zero, thus:
\( mg \cos \theta = \frac{mv^2}{r} \)
- Cancel \( m \):
\( g \cos \theta = \frac{v^2}{r} \quad \text{(Equation 2)} \)

6. Relating Equations 1 and 2:
- From Equation 1, we have \( v^2 = 2gh \).
- Substitute \( v^2 \) from Equation 2 into Equation 1:
\( g \cos \theta = \frac{2gh}{r} \)
- Cancel \( g \) (assuming \( g \neq 0 \)):
\( \cos \theta = \frac{2h}{r} \quad \text{(Equation 3)} \)

7. Expressing \( h \):
- From the geometry of the circle, we know that:
\( h = r - r \cos \theta \)
- Substitute \( \cos \theta \) from Equation 3:
\( h = r - r \left(\frac{2h}{r}\right) \)
- Simplifying gives:
\( h = r - 2h \implies 3h = r \implies h = \frac{r}{3} \)

Final Answer:
The vertical distance \( h \) below the highest point where the particle leaves the circle is:
\( h = \frac{r}{3} \)