In a large room , a person receives direct sound waves from a source 120 metres away from him. He also receives waves from the same source which reach , being reflected from the 25m high ceiling at a point halfway between them . The two waves interfere constructively for a wavelength of
20,203,205 , etc.
10,5,2.5, etc.
10,20,30, etc.
15,25,35, etc.
The correct Answer is:B
To solve the problem, we need to determine the wavelength for which the direct sound waves and the reflected sound waves interfere constructively. Here's a step-by-step solution:
Step 1: Understand the setup
We have a sound source located 120 meters away from a person. The sound waves travel directly to the person and also reflect off the ceiling (which is 25 meters high) before reaching the person.
Step 2: Determine the geometry of the situation
The distance from the sound source to the person is 120 meters. The sound reflects off the ceiling at a point halfway between the source and the person. Therefore, the distance from the source to the halfway point is:
Halfway distance=1202=60 meters
Step 3: Calculate the path of the reflected wave
The reflected wave travels from the source to the halfway point, then reflects off the ceiling, and finally travels to the person. To find the total distance traveled by the reflected wave, we can use the Pythagorean theorem.
1. The horizontal distance from the source to the halfway point is 60 meters.
2. The vertical distance from the halfway point to the ceiling is 25 meters.
Using the Pythagorean theorem:
d=√(602)+(252)
d=√3600+625
d=√4225
d=65 meters
Since the wave travels to the halfway point and back down to the person, the total distance for the reflected wave is:
Total distance=2×65=130 meters
Step 4: Determine the path difference
The path difference between the direct wave and the reflected wave is:
Path difference=Distance of reflected wave−Distance of direct wave
Path difference=130 meters−120 meters=10 meters
Step 5: Apply the condition for constructive interference
For constructive interference, the path difference must be an integral multiple of the wavelength (nλ):
Path difference=nλ
Thus, we have:
10=nλ
Step 6: Solve for the wavelength
From the equation 10=nλ, we can express the wavelength as:
λ=10n
Step 7: Find possible wavelengths
We can find different wavelengths for different integer values of n:
- For n=1: λ=10 meters
- For n=2: λ=5 meters
- For n=3: λ≈3.33 meters
- For n=4: λ=2.5 meters
Conclusion
Among the possible wavelengths, the correct answer is λ=5 meters when n=2.
Final Answer
The wavelength for which the waves interfere constructively is λ=5 meters.
---
We have a sound source located 120 meters away from a person. The sound waves travel directly to the person and also reflect off the ceiling (which is 25 meters high) before reaching the person.
The distance from the sound source to the person is 120 meters. The sound reflects off the ceiling at a point halfway between the source and the person. Therefore, the distance from the source to the halfway point is:
Halfway distance=1202=60 meters
The reflected wave travels from the source to the halfway point, then reflects off the ceiling, and finally travels to the person. To find the total distance traveled by the reflected wave, we can use the Pythagorean theorem.
2. The vertical distance from the halfway point to the ceiling is 25 meters.
d=√(602)+(252)
d=√3600+625
d=√4225
d=65 meters
Total distance=2×65=130 meters
The path difference between the direct wave and the reflected wave is:
Path difference=Distance of reflected wave−Distance of direct wave
Path difference=130 meters−120 meters=10 meters
For constructive interference, the path difference must be an integral multiple of the wavelength (nλ):
Path difference=nλ
Thus, we have:
10=nλ
From the equation 10=nλ, we can express the wavelength as:
λ=10n
We can find different wavelengths for different integer values of n:
- For n=1: λ=10 meters
- For n=2: λ=5 meters
- For n=3: λ≈3.33 meters
- For n=4: λ=2.5 meters
Among the possible wavelengths, the correct answer is λ=5 meters when n=2.
The wavelength for which the waves interfere constructively is λ=5 meters.
Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Multiple
26 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Assertion - Reasoning
6 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Subjective
24 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 24
1 Video
Similar Questions
In a hall, a person receives direct sound waves from a source 120m away. He also receives waves from the same source which reach him after being reflected from the 25m high ceiling at a point halfway between them. The two waves interfere constructively for wavelengths (in metres)
View SolutionIn a large room , a person receives direct sound waves from a source 120m away . He also receives waves from the same source which reach him after being reflected from the 5m high ceiling at a point halfway between them . For which wavelengths will these two sound waves interfere constructively ?
View SolutionIn a large room , a person receives direct sound waves from a source 120m away . He also receives waves from the same source which reach him after being reflected from the 5−m high ceiling at a point halfway between them . For which wavelengths will these two sound waves interfere constructively ?
View SolutionA detector at x=0 receives waves from three sources each of amplitude A and frequencies f+2,f and f−2.
The time at which intensity is maximum, is
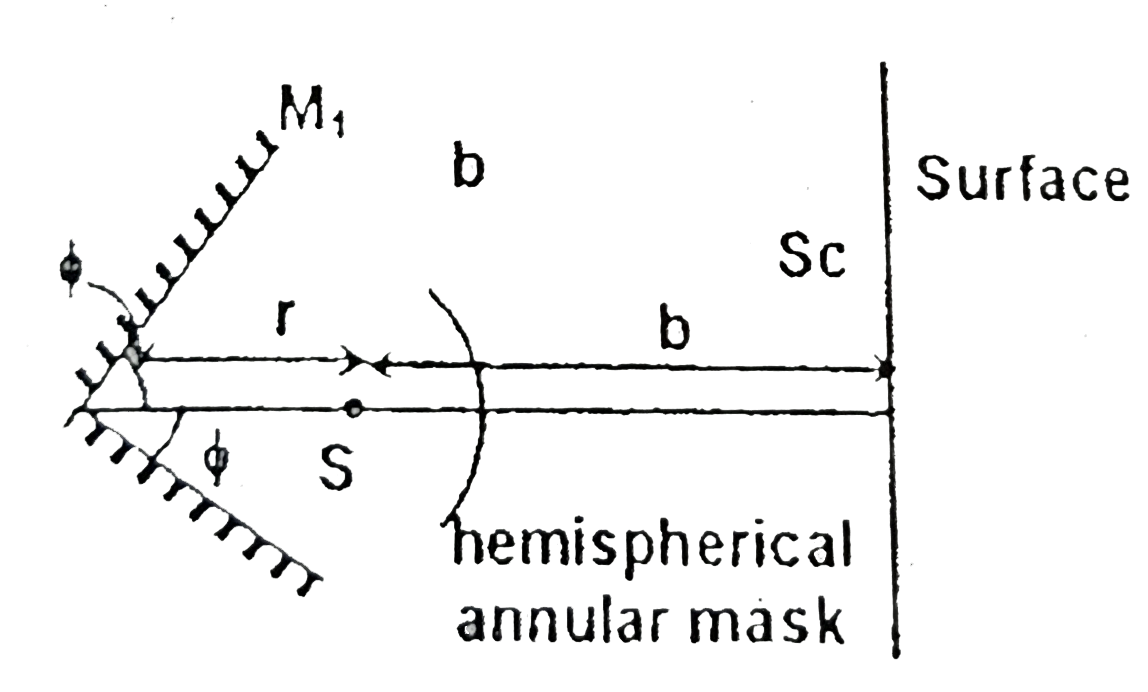
View SolutionTwo mirror M1 and M2 make an angle ϕ with line AB. A point source S is kept at a distance r from the point of intersection of mirror. A small hemispherical annular mask is kept close to S so that no ray emanting from S directly reaches the screen kept at a distance b from the source. Interference pattern of rays reflected from M1 and M2 is oberved on the screen. Find the fringe width of this interference pattern λ= wavelength of light being emitted by source.
View SolutionA cylinderical tube, open at one end and closed at the other, is in acoustic unison (resonance) with an external source of sound of singal frequency held at the open end of the tube, in its fundamental note.
Then :
A. the displacement wave from the source gets reflected with a phase change of π at the closed end
B. the pressrue wave from the source get reflected without a phase change at the closed end
C. the wave reflected from the closed and again gets reflected at the open end
D. the wave reflected from the closed end does not suffer reflection at the open end
View SolutionAn electromagnetic wave emitted by source travels 21 km to arrive at a receiver. The wave while travelling in another path is reflected from a surface at 19 km away and further travels 12 km to reach the same receiver. If destructive interference occurs at the receiving end, the mximum wavelength of the wave is
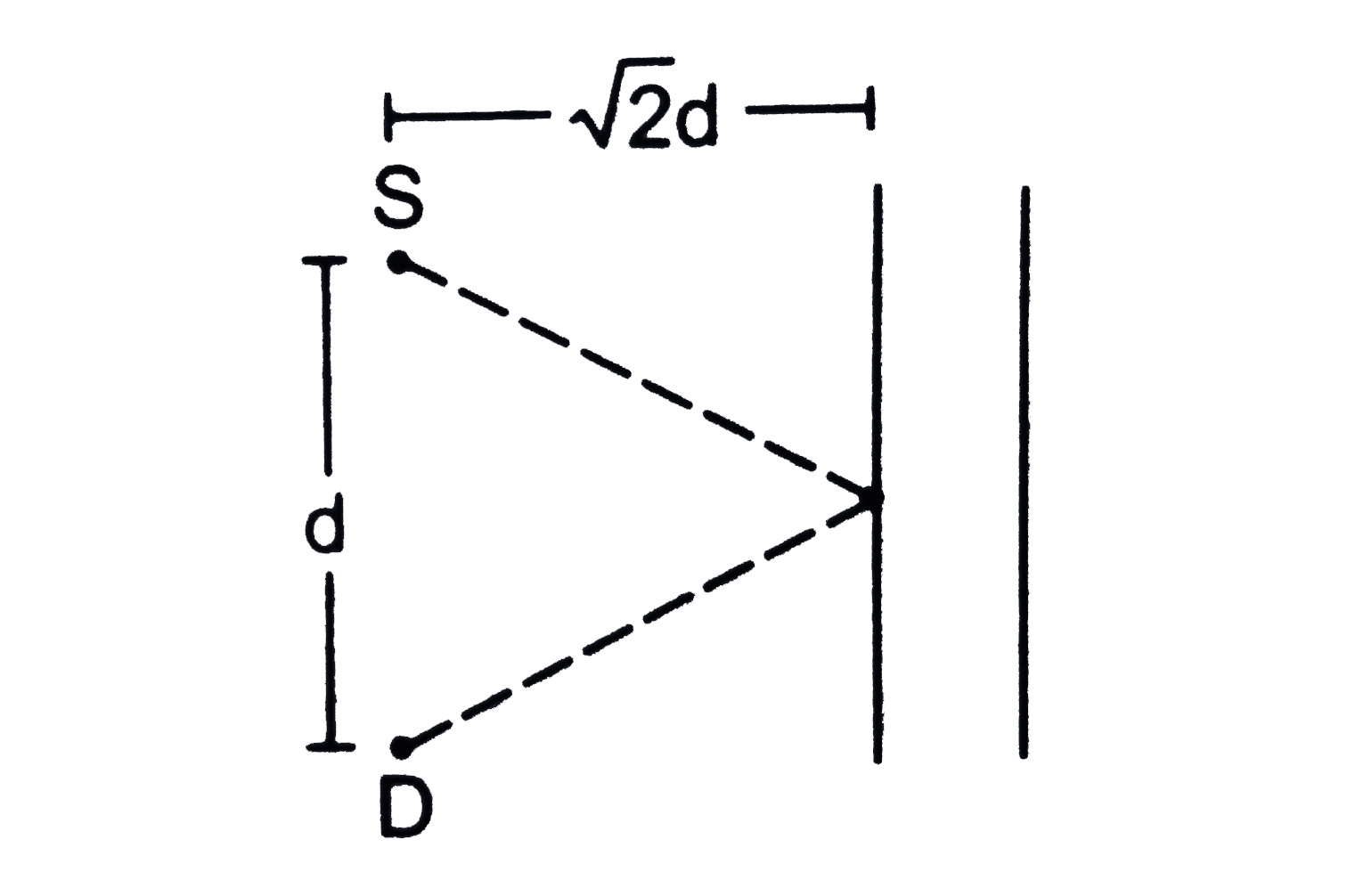
View SolutionA source S and a detector D are placed at a distance d apart. A big cardboard is placed at a distance √2d from the source and the detector as shown in figure. The source emits a wave of wavelength =d2 which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave ?
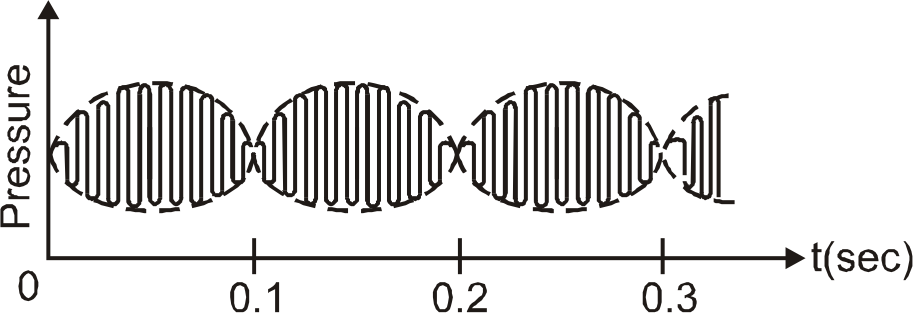
View SolutionTwo sound waves are superimposed. The resulting pressure variation at a single point at a distance 'x' from the source is graphed below :
The beat frequency of the resulting sound wave is :
View SolutionThe path length difference between two waves coming from coherent sources for destructive interference should be
View Solution
