In a large room , a person receives direct sound waves from a source 120m away . He also receives waves from the same source which reach him after being reflected from the 5−m high ceiling at a point halfway between them . For which wavelengths will these two sound waves interfere constructively ?
To solve the problem step by step, we need to determine the conditions for constructive interference of the sound waves reaching the person from the source directly and after reflection from the ceiling.
Step 1: Understand the Setup
- The source of sound is located 120m away from the person.
- The sound wave reflects off a ceiling that is 5m high at a point halfway between the source and the person.
Step 2: Determine the Path Lengths
- The direct path length from the source to the person is 120m.
- The reflected path involves two segments:
1. From the source to the midpoint (which is 60m).
2. From the midpoint to the ceiling and then back down to the person.
Step 3: Calculate the Length of the Reflected Path
- The height of the ceiling is 5m, and the horizontal distance to the midpoint is 60m.
- Using the Pythagorean theorem, the length of the reflected path (hypotenuse) can be calculated:
\(
\text{Reflected path length} = \sqrt{(60)^2 + (5)^2} = \sqrt{3600 + 25} = \sqrt{3625} \approx 60.41 \text{ m}
\)
- Since the sound travels to the ceiling and back, the total length of the reflected path is:
\(
\text{Total reflected path} = 2 \times 60.41 \approx 120.82 \text{ m}
\)
Step 4: Calculate the Path Difference
- The path difference between the direct path and the reflected path is:
\(
\text{Path difference} = \text{Total reflected path} - \text{Direct path} = 120.82 \text{ m} - 120 \text{ m} = 0.82 \text{ m}
\)
Step 5: Condition for Constructive Interference
- For constructive interference, the path difference must be an integer multiple of the wavelength (\( \lambda \)):
\(
\text{Path difference} = n \lambda
\)
where \( n \) is an integer.
Step 6: Solve for Wavelengths
- Rearranging the equation gives:
\(
\lambda = \frac{0.82}{n}
\)
- For different integer values of \( n \):
- For \( n = 1 \): \( \lambda = 0.82 \text{ m} \)
- For \( n = 2 \): \( \lambda = 0.41 \text{ m} \)
- For \( n = 3 \): \( \lambda = 0.273 \text{ m} \)
- And so on...
Final Answer
The wavelengths for which the two sound waves will interfere constructively are:
- \( \lambda = \frac{0.82}{n} \) for \( n = 1, 2, 3, \ldots \)
- The source of sound is located 120m away from the person.
- The sound wave reflects off a ceiling that is 5m high at a point halfway between the source and the person.
- The direct path length from the source to the person is 120m.
- The reflected path involves two segments:
1. From the source to the midpoint (which is 60m).
2. From the midpoint to the ceiling and then back down to the person.
- The height of the ceiling is 5m, and the horizontal distance to the midpoint is 60m.
- Using the Pythagorean theorem, the length of the reflected path (hypotenuse) can be calculated:
\(
\text{Reflected path length} = \sqrt{(60)^2 + (5)^2} = \sqrt{3600 + 25} = \sqrt{3625} \approx 60.41 \text{ m}
\)
- Since the sound travels to the ceiling and back, the total length of the reflected path is:
\(
\text{Total reflected path} = 2 \times 60.41 \approx 120.82 \text{ m}
\)
- The path difference between the direct path and the reflected path is:
\(
\text{Path difference} = \text{Total reflected path} - \text{Direct path} = 120.82 \text{ m} - 120 \text{ m} = 0.82 \text{ m}
\)
- For constructive interference, the path difference must be an integer multiple of the wavelength (\( \lambda \)):
\(
\text{Path difference} = n \lambda
\)
where \( n \) is an integer.
- Rearranging the equation gives:
\(
\lambda = \frac{0.82}{n}
\)
- For different integer values of \( n \):
- For \( n = 1 \): \( \lambda = 0.82 \text{ m} \)
- For \( n = 2 \): \( \lambda = 0.41 \text{ m} \)
- For \( n = 3 \): \( \lambda = 0.273 \text{ m} \)
- And so on...
The wavelengths for which the two sound waves will interfere constructively are:
- \( \lambda = \frac{0.82}{n} \) for \( n = 1, 2, 3, \ldots \)
Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Exercise 7.2
32 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Subjective
24 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 24
1 Videos
Similar Questions
In a hall, a person receives direct sound waves from a source 120m away. He also receives waves from the same source which reach him after being reflected from the 25m high ceiling at a point halfway between them. The two waves interfere constructively for wavelengths (in metres)
View SolutionIn a large room , a person receives direct sound waves from a source 120 metres away from him. He also receives waves from the same source which reach , being reflected from the 25m high ceiling at a point halfway between them . The two waves interfere constructively for a wavelength of
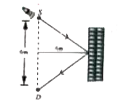
View SolutionA person standing at a distance of 6 m from a source of sound receives sound wave in two ways, one directly from the source and other after reflection from a rigid boundary as shown in the figure. The maximum wavelength for which, the person will receive maximum sound intensity, is
View SolutionA detector at x=0 receives waves from three sources each of amplitude A and frequencies f+2,f and f−2.
The time at which intensity is maximum, is
View SolutionThe sound level at a point 5.0 m away from a point source is 40 dB. What will be the level at a point 50 m away from the source ?
View SolutionTwo coherent sources A and B of radio waves are 5.00 m apart. Each source emits waves with wavelength 6.00m. Consider points along the line between the two sources. At what distances, if any, from A is the interference (a) constructive (b) destructive?
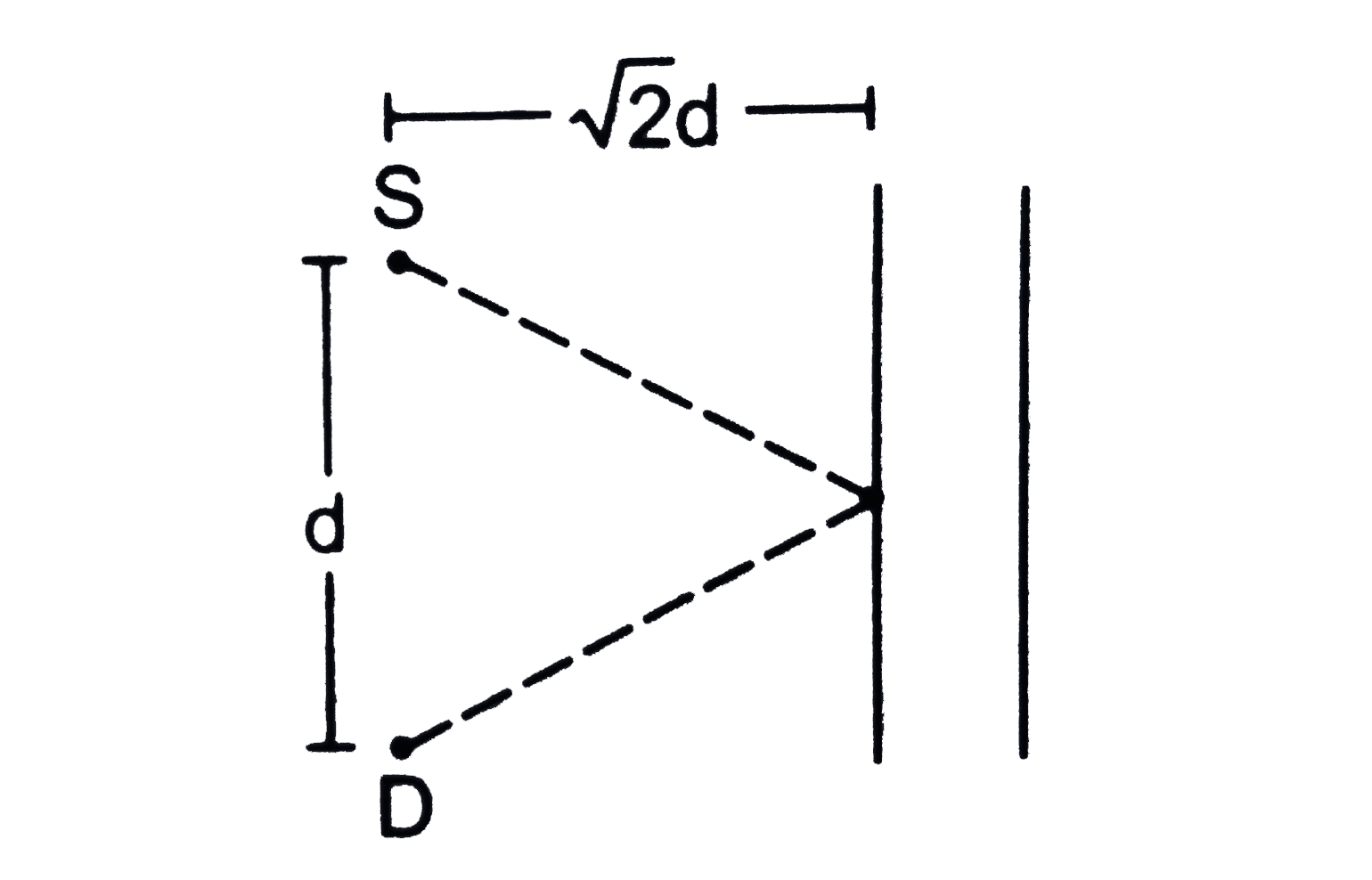
View SolutionA source S and a detector D are placed at a distance d apart. A big cardboard is placed at a distance √2d from the source and the detector as shown in figure. The source emits a wave of wavelength =d2 which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave ?
View SolutionA sound wave starting from source S, follows two paths AOBandACB to reach the detector D. If ABC is an equilateral traingle , of side l and there is silence at point D, the maximum wavelength (λ) of sound wave must be

View SolutionAn electromagnetic wave emitted by source travels 21 km to arrive at a receiver. The wave while travelling in another path is reflected from a surface at 19 km away and further travels 12 km to reach the same receiver. If destructive interference occurs at the receiving end, the mximum wavelength of the wave is
View SolutionA man standing 25 m away from a wall produces a sound and receives the reflected sound.
Calculate the time after which he receives the reflected sound if the speed of sound in air is 350 m s−1.
View Solution
