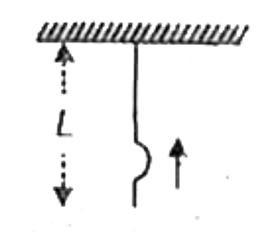
It is stated in the previous problem that a pilse travels from the bottom to the top of a hanging rope of length L in the time interval Δ=2√Lg. Use this result to answer the following question. (It is not neccesary to set up any new integrations.) (a) over what time interval does a pulse travel halfway up the rope? Give your answer as a fraction of the quantity 2√Lg. (b) A pulse starts travelling up the rope. how far it travelled after a time interval √Lg)?
The wave pulse travels faster as it goes up the rope because the tension higer in the rope is greater (to support the weight of the rope below it ). Therefore it should take mote than half the total time Δt for the wave to travel halfway up the rope. likewise, the pulse should travel less than halfway up the rope in time Δt/2.
By using the time relationship given in the problem and making suitable substitution, we can find the required time and distance.
(a) From the equation given, the time for a pulse to pulse to travel any distance, d, up from the bottom of the rope is Δtd=2√d/(g). so the time for a pulse to travel a distance L/2 from the botom is Δt1/2=2√L2g=0.707(2√Lg)
(b) Likewise, the distance a pulse a pulse travels from the bottom of a rope in a time Δtd is d=(gΔt2d. so the distance travelled by a pulse after a time
Δd=√Lgisd=g(L/g)4=L4
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Example
9 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.1
9 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
Study the experimental set-up given below and answer the following questions:
What is your observation for flasks .A. and .B.?
View Solutionln=∫xn√a2−x2dx, then answer the following questions:
The value of l1 is
View SolutionThe velocity time graph of a particle moving along a straight line is shown in the figure. In the time interval from t=0 to t=8 second, answer the following three question.

The distance travelled by the particle is :
View SolutionA pulse is generated at lower end to a hanging rope of uniform density and length L. The speed of the pulse when it reaches the mid point of rope is
View SolutionShow that the expression of the time period T of a simple pendulum of length l given by T=2π√lg is dimensionally currect
View SolutionShow that the expression of the time period T of a simple pendulum of length l given by T=2π√lg is dimensionally correct
View SolutionA uniform rope of mass m and length L hangs from a celling. (a) Show that the speed of a transverse wave on the rope is a function of y, the distance from the lower end, and is given by t=2√L/g.
View SolutionThe displacement of a moving object in a given interval of a time is zero. Would the distance travelled by the object also be zero ? Justify your answer ?
View SolutionA heavy but unifrom rope of length L is suspended from a celling . A particle is dropped from the celling at the instant when the bottom end is given a transverse wave pulse. Where will the particle meet the pulse.
View SolutionThe time period T of oscillation of a simple pendulum of length l is given by T=2π.√lg.
Find the percentage error in T corresponding to
(i) on increase of 2% in the value of l.
(ii) decrease of 2% in the value of l.
View Solution
