A heavy but unifrom rope of length L is suspended from a celling . A particle is dropped from the celling at the instant when the bottom end is given a transverse wave pulse. Where will the particle meet the pulse.
at a distance 2l3 form the bottom
at a distance L3 from the bottom
at a distance 3L4 from the bottom
none of the above
The correct Answer is:B
Step by step video & image solution for A heavy but unifrom rope of length L is suspended from a celling . A particle is dropped from the celling at the instant when the bottom end is given a transverse wave pulse. Where will the particle meet the pulse. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - More Than One Option is Correct23videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Comprehion Type Questions20videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE MAINS50videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery9videos
VECTORS
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based2videos
WORK, ENERGY & POWER
Similar Questions
A heavy but uniform rope of lenth L is suspended from a ceiling. (a) Write the velocity of a transverse wave travelling on the string as a function of the distance from the lower end. (b) If the rope is given a sudden sideways jerk at the bottom, how long will it take for the pulse to reach teh celling ? (c ) A particle is dropped from the ceiling at the instant the bottom end is given the jerk where will the particle meet the pulse ?
View SolutionA heavy particle hanging from a string of length I is projected horizontally with speed √gl . Find the speed of the particle at the point where the tension in the string equals weight of the particle.
View SolutionA uniform string of length 'L' is suspended from a point on the ceiling. A small wave pulse is now introduced at its lowest end and it starts moving up towards the ceiling.
(i) What will be the speed of the wave pulse when it has moved up a distance x?
(ii) How much time does this wave pulse take to reach the ceiling?View SolutionA heavy rope is suspended from a rigid support A wave pulse is set up at the lower end, then
View SolutionA heavy rope is suspended from a rigid support A wave pulse is set up at the lower end, then
View SolutionA rope of length L is pulled by a constant force F. What is the tension in the rope at a distance x from the end where the force is applied ?
View SolutionA mass of 6 kg is suspended by a rope of length 2m from a celling. A force of 50N is applied in horizontal direction at the mid point of the rope. What is the angle of the rope with the verticle in equilibrium:-
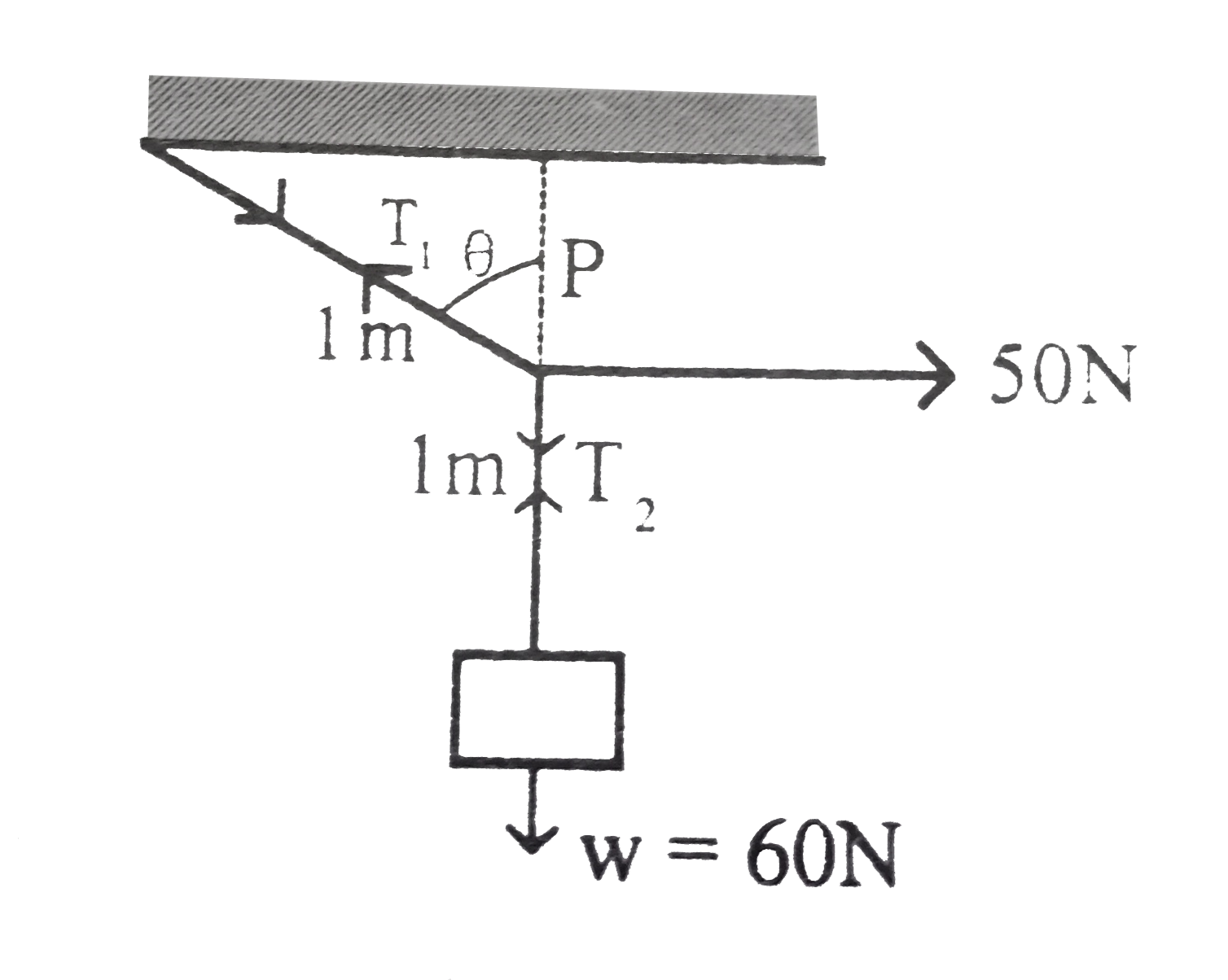 View Solution
View SolutionA metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
View SolutionA uniform string of length 20m is suspended from a rigid support. A short wave pulse is introduced at its lowest end. It starts moving up the string. The time taken to reach the support is :
(take g=10ms−2)View SolutionA uniform string of length 10 m is suspended from a rigid support A short wave pulse is introduced at its lowest end it starts moving up the string the time taken to reach the support is (take g=10m/sec2)
View Solution


