
A cylinderical block of density d stays fully immersed in a beaker filled with two immiscible liquids of different densities d1 and d2 The block is in equilibrium with half of it in liquid 1 and the other half in liquid 2 as shown in the Fig. If the block is given a displacement downwards released, then neglecting friction study the following statements.
It executes simple harmonic motion.
Its motion is periodic but not simple harmonic.
The frequency of oscillation is independent of the size of the cylinder.
The displacement of the centre of the cylinder is symmetric about its equilibrium position.
The correct Answer is:A, D
since liquid 2 is below liquid 1, liquid 2 is denser than liquid 1. Let area of cross section of the cylindrical block be A and it be displaced downwards by y. then volume of liquid 2 displaced will get increases by Ay and that of liquid 1 will get decreased by the same amount Ay. Hence net increase in upthrust on the block will be equal to (Ayd2g−Ayd1g). This additional upthurust tries to restore the block in original position.
It means, the block experiences a restoring force Ay(d2−d1)g. Since this force is restoring and directly proportional to displacement y, it will execute SHM along a vertical line.
Hence, option (a) is correct and option (b) is wrong. If mass of the block is equal to m, then its acceleration will be equal to ltbr> Ayg(d2−d1)m.
Since its acceleration depends on mass m, frequency of oscillation will depend on size of the cylinder. Hence option (c ) is wrong. If the cylinder is displaced upward through y from equilibrium position, then it will experience a net downward force, equal to calculated above. This shows that its motion will be symmetric about its equilibrium position.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Comprehension
33 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single Correct
107 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A cubical block of density ρ floats completely immersed in two non-mixing liquids of densities ρ1andρ2 as shown in figure. The relation between ρ,ρ1andρ2 is :
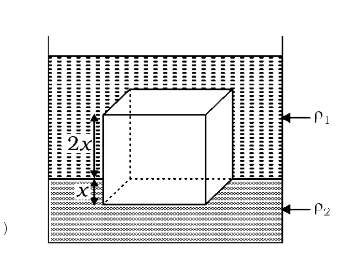
View SolutionIf two liquids of same volume but different densities ρ1 and ρ2 are mixed, then the density of the mixture is:
View SolutionA vertical pole of length l , density ρ , area of cross section A floats in two immiscible liquids of densities ρ1and ρ2. In equuilibrium possition the bottom end is at the interface of the liquids. When the cylinder is displaced vertically, find the time period of oscillation.
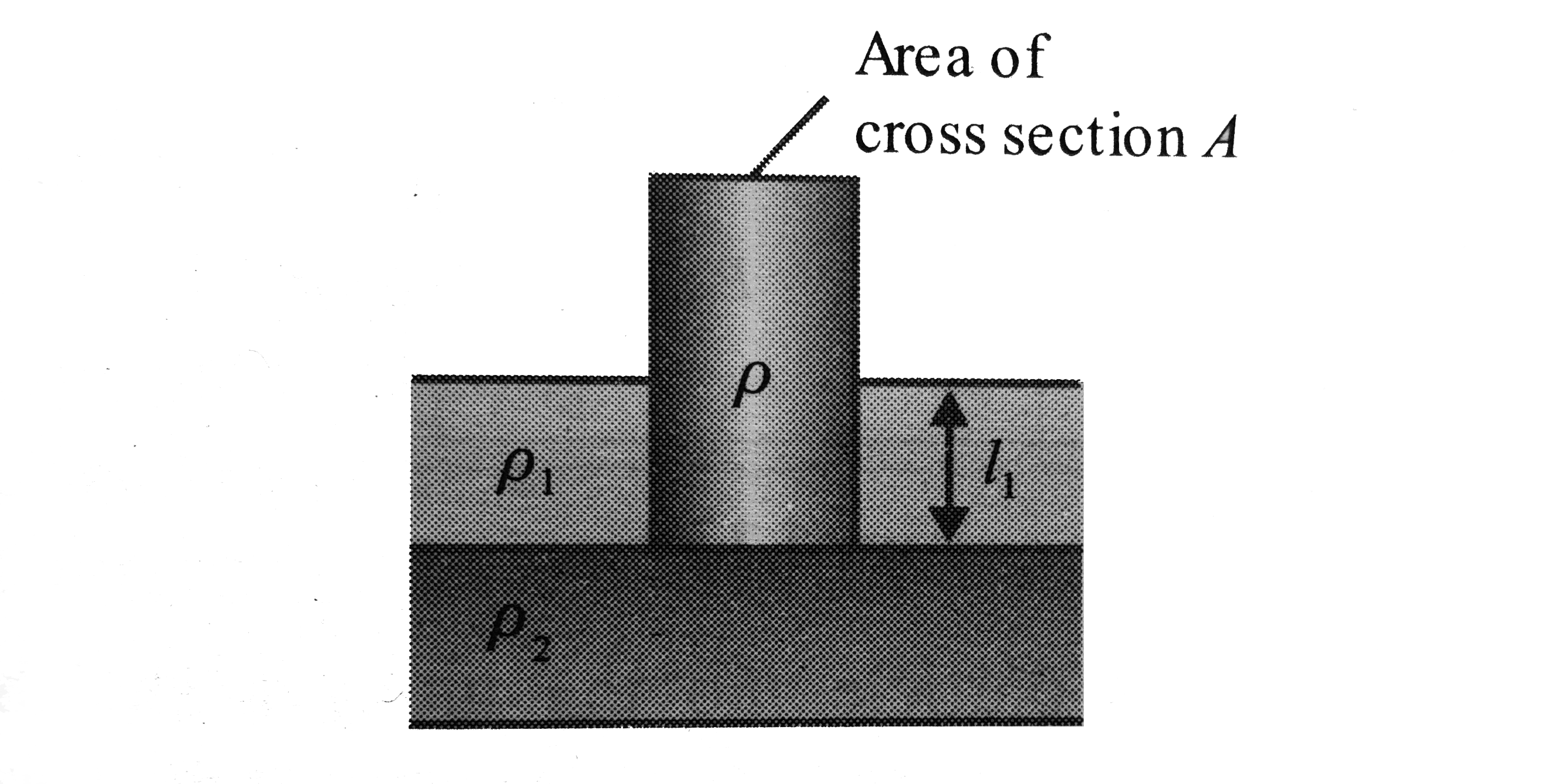
View SolutionA large tank is filled with two immiscible liquids of densities ρ1andρ2 A small hole is made at the base of the tank and liquid of density ρ2 starts flowing out of it. Three points A, B and C are marked on a vertical line. Velocity with which liquid leaves the hole is :
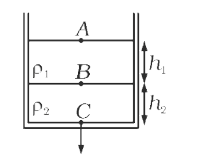
View SolutionA beaker is filled with two immiscible transparent liquids of refractive indices μ1 and μ2 having thickness of layers d1 and d2 respectively. The apparent depth of the bottom of the beaker is
View SolutionA cylindrical block of the density ρ is partically immersed in a liwuid of density 3ρ. The plane surface of the block remains parallel to the surface of the liquid. The height of the block is 60m. The block perform SHM when displaced form its mean position [Use g=9.8m/s2]
View SolutionIf equal masses of two liquids of densities d1andd2 are mixed together, the density of the mixture is
View SolutionThe figure represents a U-tube of uniform cross-section filled with two immiscible liquids. One is water with density ρw and the other liquid is of density ρ . The liquid interface lies 2cm above the base. The relation between ρ and ρw is
 .
.
View SolutionA vessel is filled with two different liquids of densities ρand2ρ respectively as shown in the figure. The velocity of flow of liquid through a hole at height h2 from bottom is
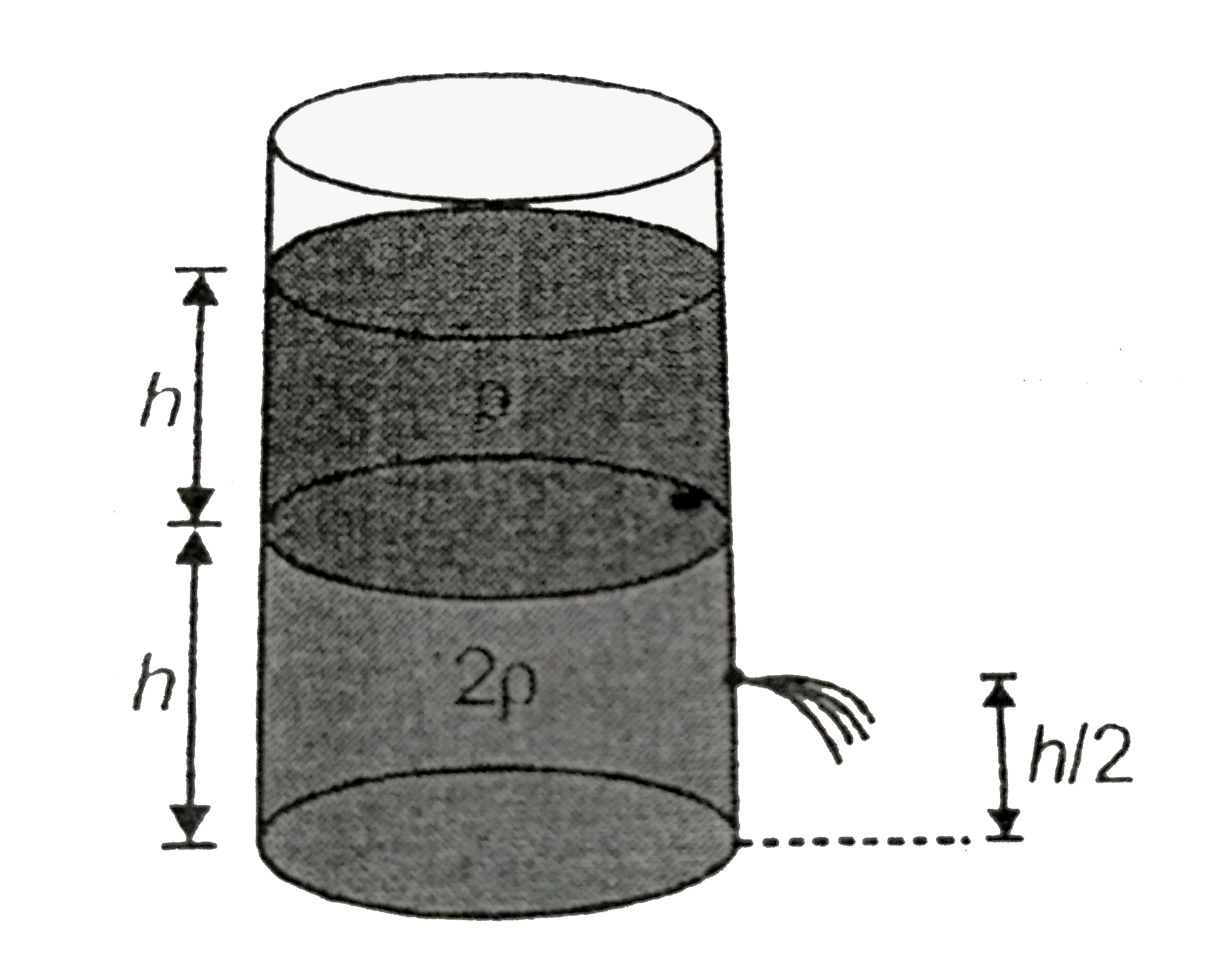
View SolutionA solid cylinder of length L is in equilibrium in two different liquid A and B as shown in the figure.The density of liquid A 3ρ2 and liquid B is 3ρ.The density of cylinder is
View Solution
