figure (a) and (b) represent spring- block system. If m is displacement slightly , find the time period of ascillation of the system.
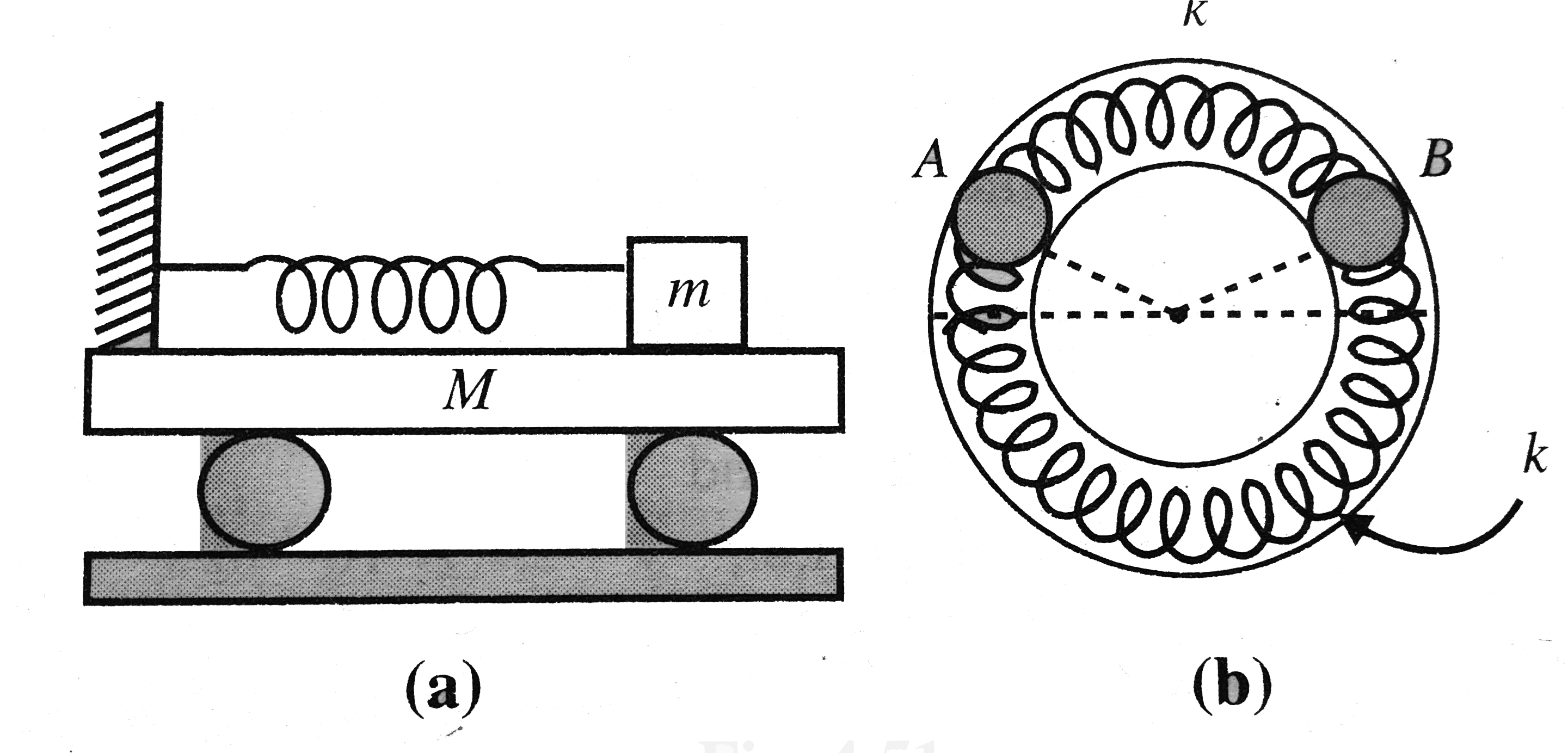
both the cases are as follows:
Reduced mass of the system Reduced mass of the system
μ=(mMm+m) μ=mMm+m=m2
T=2π√μk and ke=k+k=2k
T=2π√μke
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Solved Example
15 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.1
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
Find the period of oscillation of the system shown in figure.

View SolutionSpring mass system is shown in figure. find the time period of vertical oscillations. The system is in vertical plane.

View SolutionIn spring-block system match the following

View SolutionA pendulum makes perfectly elastic collision with block of m lying on a frictionless surface attached to a spring of force constant k. Pendulum is slightly displaced and released. Time period of oscillation of the system is
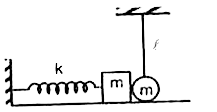
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is

View SolutionA system is shown in the figure. The force The time period for small oscillations of the two blocks will be

View SolutionTime period of a given spring-mass system is

View SolutionIn a spring-block system, match the following:
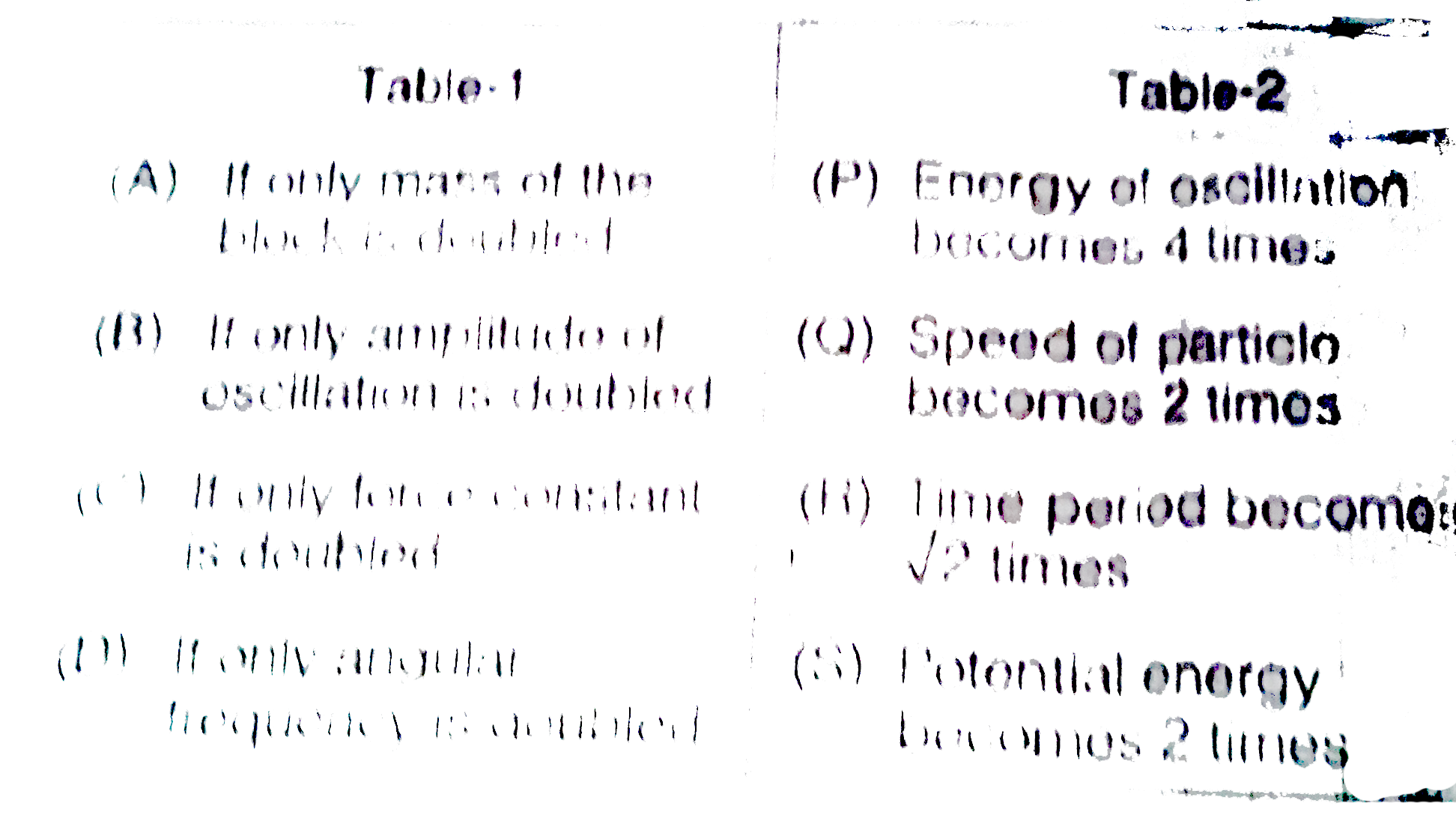
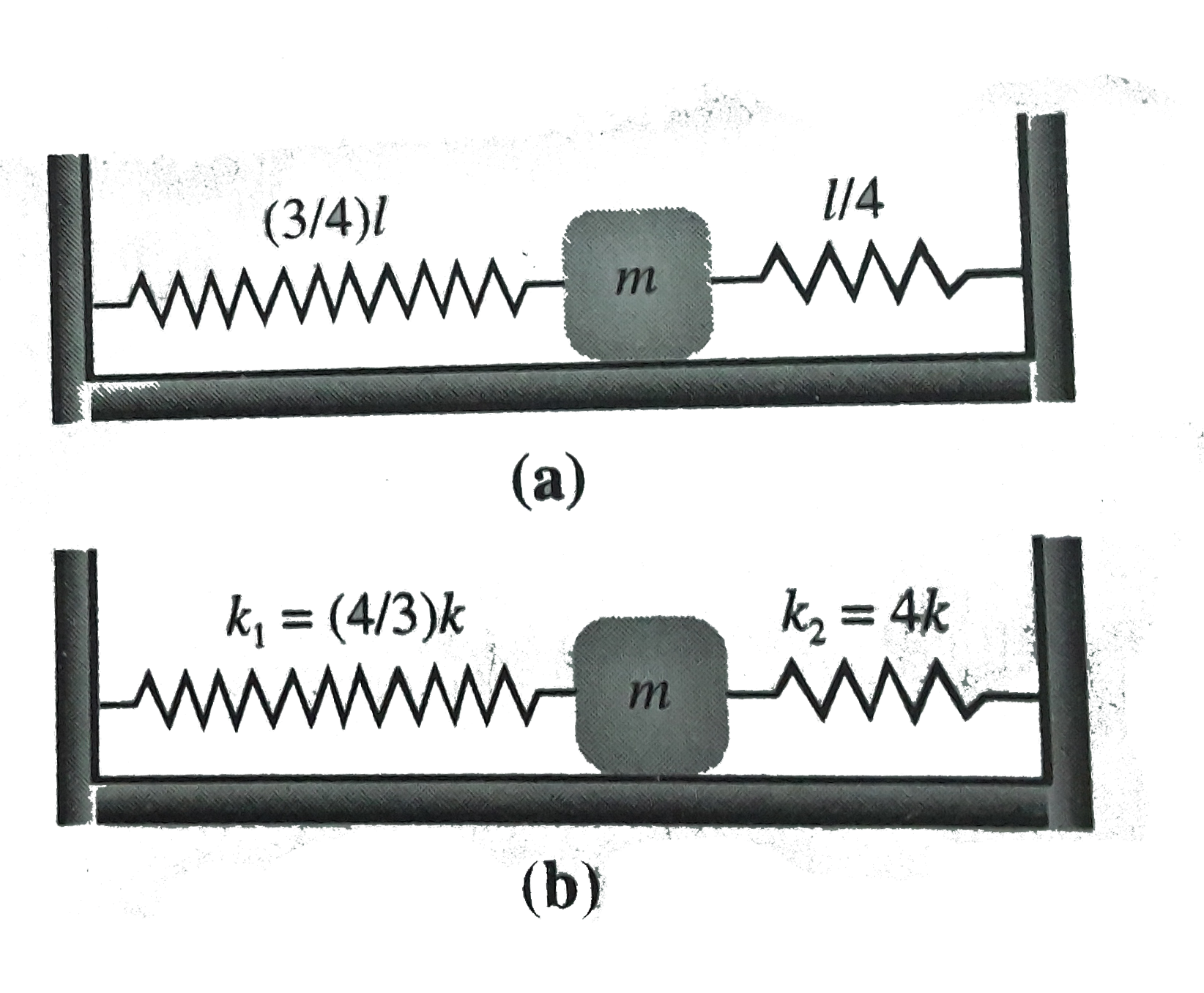
View SolutionA spring of stiffness constant k and natural length l is cut into two parts of length 3l/4andl/4, respectively, and an arrangement is made as shown in figure . If the mass is slightly displaced , find the time period of oscillation.
View Solution
