One mole of an ideal monatomic gas udnergoes thermodynamic cycle 1→2→3→1 as shown in figure. Initial temperature of gas in T0=300K.
Process 1→2:P=aV
Process 2→3:PV= Constant
Process 3→1:P= Constant
( Take 1n|3|=1.09)
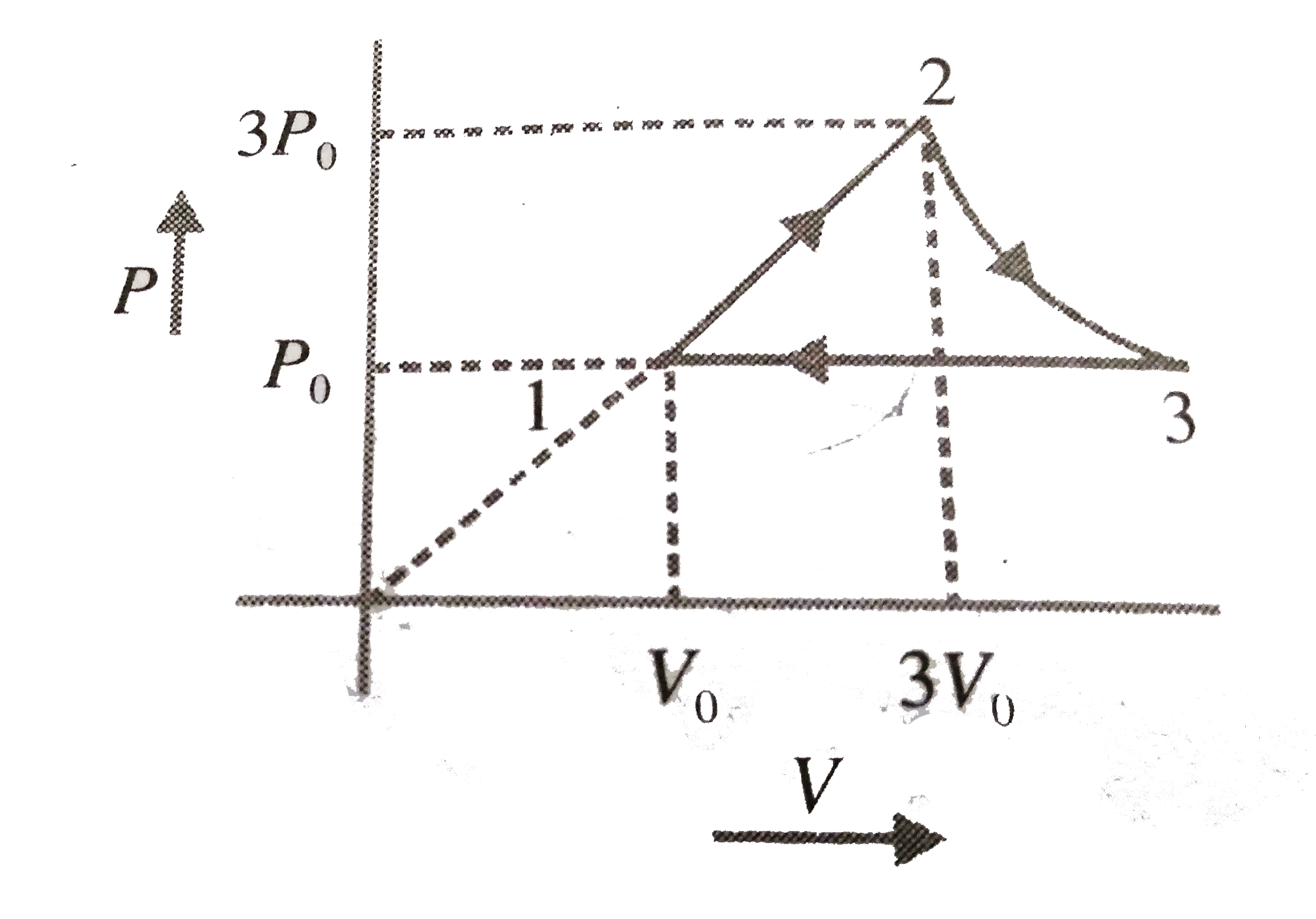
Determine the heat capacity of 3-1 process.
20.75J/mol−K
10.23J/molK
22.37J/mol−K
15.96J/mol−K
The correct Answer is:A
For process 1→2
W12=∫21αVdV=α∫3V0V0VdV=α2(9V20−V20)
=4αV20
Using gas law, P1V1T1=P2V2T2
T2=P2V2P1V1T1=V22V21T1=(3V0V0)2T0=9T0
For process 2→3
W23=RT2log∣∣∣P2p3∣∣∣=R(9T0)log∣∣∣3P0P0∣∣∣
=9RT0log|3|=9.81RT0
For isothermal process:P2V2=P3V3
Therefore, V3=P2V2P3=3P0P0(3V0)=9V0
Also, W31=P0(V1−V3)=P0(V0−9V0)=−8P0V0
=−8RT0
Applying gas law in process 1→2
P0V0=RT0 orαV20=RT0
The net work is
Wnet=W12+W23+W31
=4RT0+9.81RT0−8RT0 ltbr> =5.81RT0
For process 1→2
ΔU12=CV(T2−T1)
=4RT0+12RT0=16RT0
Since
ΔU12=C12(T2−T1)=8C12T0
C12=2R=16.6J/mol−K
For the process 2→3:C23=∞
For the process 3→1:C31=CP+R
=5R/2=2075J/mol−K
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Assertion-Reasoning
6 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
Similar Questions
One mole of an ideal monatomic gas udnergoes thermodynamic cycle 1→2→3→1 as shown in figure. Initial temperature of gas in T0=300K.
Process 1→2:P=aV
Process 2→3:PV= Constant
Process 3→1:P= Constant
( Take 1n|3|=1.09)
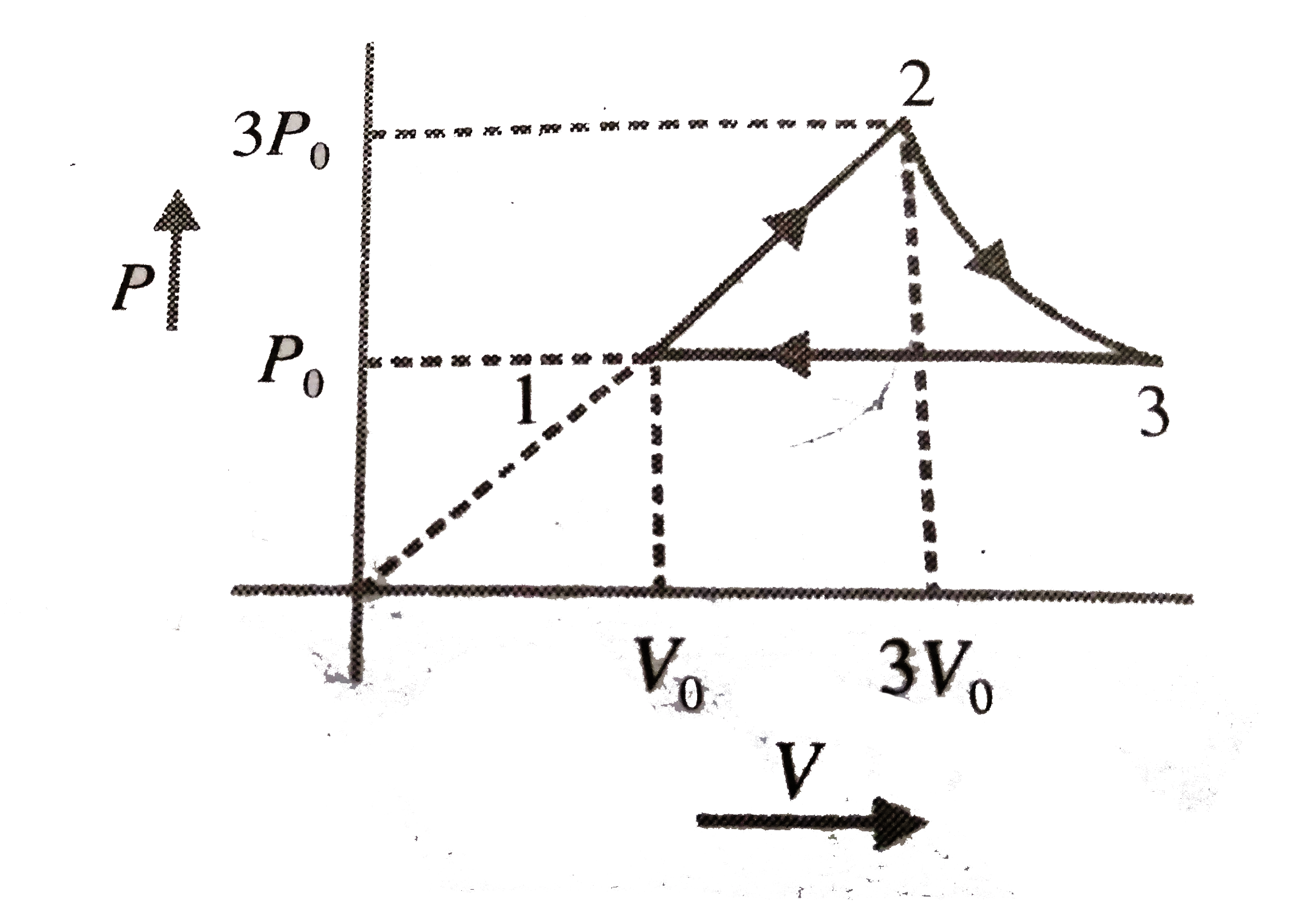
Find the net work done by the cycle.
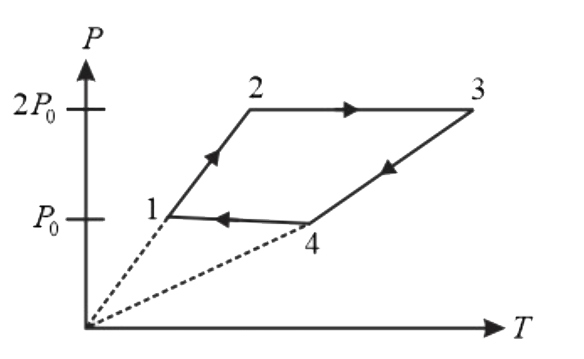
View SolutionOne mole of an ideal monoatomic gas undergoes a cyclic process, as shown in the figure. If the temperature of the gas at state 1 is 300 K and at state 4 is 500 K, then heat exchanged during process 2→3, is
View SolutionOne mole of an ideal monoatomic gas undergoes a cyclic process as shown in figure . Temperature at point 1 =300K and process 2−3 is isothermal .
_S01_113_O01.png) .
.
Net work done by gas in complete cycle is
View SolutionAn ideal monatomic gas undergoes process PV1.25 = constant .Then
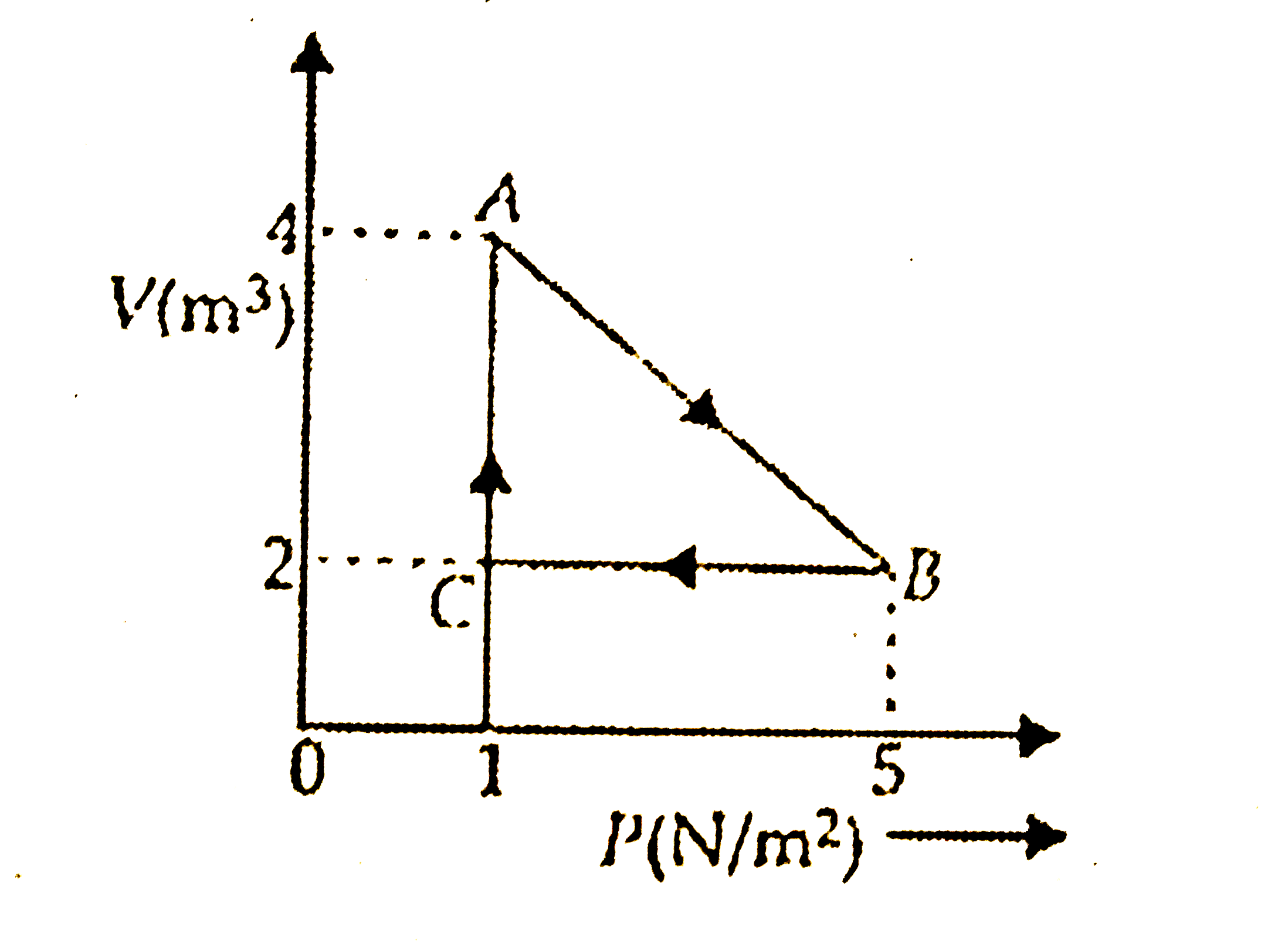
View SolutionAn ideal gas is taken through the cycle A→B→C→A, as shown in figure. If the net heat supplied to the gas in the cycle is 5 J the work done by the gas in the process A→B is
View SolutionOne mole of a monatomic gas is taken from a point A to another point B along the path ACB. The initial temperature at A is T0. Calculate the heat abosrbed by the gas in the process A→C→B.

View SolutionOne mole of a monatomic gas is taken from a point A to another point B along the path ACB. The initial temperature at A is T0. Calculate the heat abosrbed by the gas in the process A→C→B.

View SolutionA heat engine carries one mole of an ideal mono-atomic gas around the cycle as shown in the figure below. Process 1→2 takes place at constant volume, process 2→3 is adiabatic and process 3→1 takes place at constant pressure. Then the amount of heat added in the process 1→2 is
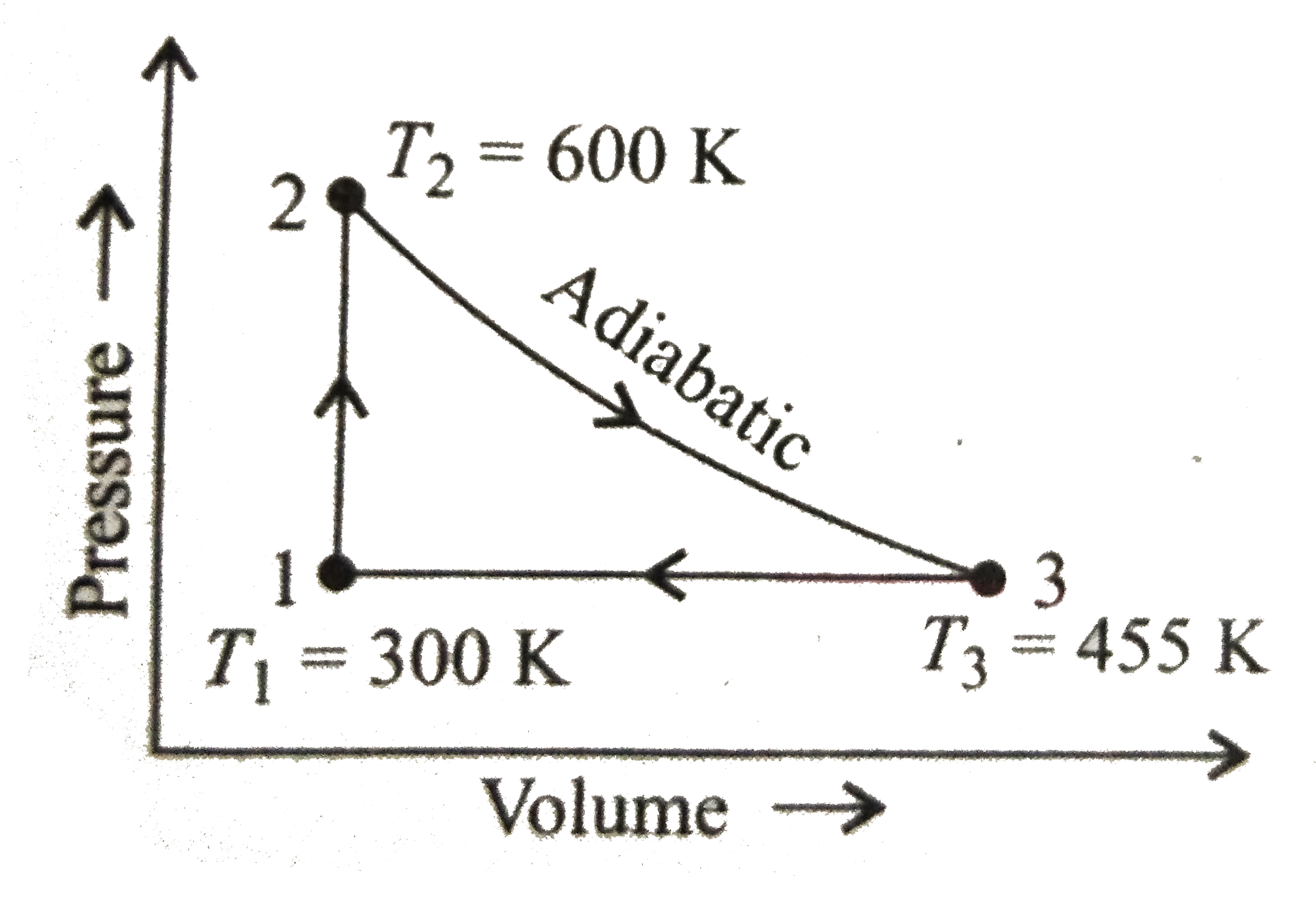
View SolutionOne mole of an ideal monatomic gas undergoes a process described by the equation PV3= constant. The heat capacity of the gas during this process is
View SolutionOne mole of an ideal gas undergoes a process
p=p01+(VV0)2
where p0and V0 are constants. Find temperature of the gaas when V=V0.
View Solution