A stationary cylinder of oxygent used in a hospital has the following characteristics at room temperature 300K, gauge pressure 1.38×107 Pa. volume 16L. If the flow area, measured at atmospheric pressure, is constant at 2.4L/min, the cylinder will last for nearly
5h
10h
15h
20h
The correct Answer is:C
To solve the problem step by step, we will use the ideal gas law and the information provided about the cylinder of oxygen.
Step 1: Convert the volume of the cylinder from liters to cubic meters.
Given:
- Volume V1=16L=16×10−3m3
Step 2: Identify the initial conditions.
- Initial temperature T=300K
- Initial pressure P1=1.38×107Pa
- Final pressure P2=Patm=105Pa
Step 3: Set up the equation using the ideal gas law.
Since the process is isothermal (constant temperature), we can use the relationship:
P1V1=P2V2
Where V2 is the volume of gas that flows out of the cylinder over time t.
Step 4: Express V2 in terms of flow rate and time.
Given the flow rate:
- Flow rate = 2.4L/min=2.4×10−3m3/min
Thus,
V2=Flow rate×t=(2.4×10−3)×t
Step 5: Substitute V2 into the ideal gas equation.
Substituting V2 into the equation:
P1V1=P2(2.4×10−3×t)
Step 6: Rearrange the equation to solve for t.
Rearranging gives:
t=P1V1P2×2.4×10−3
Step 7: Plug in the values and calculate t.
Substituting the known values:
t=(1.38×107)×(16×10−3)(105)×(2.4×10−3)
Calculating:
t=(1.38×107)×(16×10−3)(105)×(2.4×10−3)
t=(1.38×16)×1042.4
t=22.08×1042.4
t=9.2×103 minutes
t≈920 minutes
Step 8: Convert minutes to hours.
t≈92060≈15.33 hours
Conclusion
The cylinder will last for nearly 15 hours.
---
Given:
- Volume V1=16L=16×10−3m3
- Initial temperature T=300K
- Initial pressure P1=1.38×107Pa
- Final pressure P2=Patm=105Pa
Since the process is isothermal (constant temperature), we can use the relationship:
P1V1=P2V2
Where V2 is the volume of gas that flows out of the cylinder over time t.
Given the flow rate:
- Flow rate = 2.4L/min=2.4×10−3m3/min
V2=Flow rate×t=(2.4×10−3)×t
Substituting V2 into the equation:
P1V1=P2(2.4×10−3×t)
Rearranging gives:
t=P1V1P2×2.4×10−3
Substituting the known values:
t=(1.38×107)×(16×10−3)(105)×(2.4×10−3)
t=(1.38×107)×(16×10−3)(105)×(2.4×10−3)
t=(1.38×16)×1042.4
t=22.08×1042.4
t=9.2×103 minutes
t≈920 minutes
t≈92060≈15.33 hours
The cylinder will last for nearly 15 hours.
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Multiple Corrects
Explore 29 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Assertion-Reasoning
Explore 6 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Subjective
Explore 22 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Single correct anwer type
Explore 14 Videos
Similar Questions
A cylinder of cross-section area. A has two pistons of negligible mass separated by distances l loaded with spring of negligible mass. An ideal gas at temperature T1 is in the cylinder where the springs are relaxed. When the gas is heated by some means its temperature becomes T2 and the springs get compressed by l2 each . if P0 is atmospheric pressure and spring constant k=2P0Al, then find the ratio of T2 and T1 .
_S01_124_Q01.png)
View SolutionContainer A holds an ideal gas at a pressure 1×105 Pa and at 300 K. Container B whose volume is 4 times the volume of A has the same ideal gas at 400 K and at a pressure of 5×105
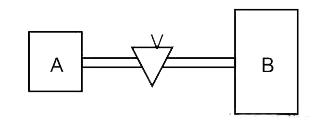
The valve V is adjusted to allow the pressure to equalize, but the temperature of each container is kept constant at the initial value, then the pressure in the two containers is :
View SolutionA closed vessel of volume 0.2m3 contain hydrogen gas at temperature 300K and pressure 105Pa. Then the heat required to raise temperature to 600K is:(molar heat capacity of hydrogen at constant volume is 5cal/mol−K)
View SolutionAn iron cylinder contains helium at a pressure of 250 k Pa at 300 K. The cylinder can withstand a pressure of 1×106 Pa. The room in which cylinder is placed catches fire. Predict the temperature (in K) at which the cylinder will blow up before it melts or not (m.p.t. of the cylinder =1800K)..
View SolutionThe presssure of the gas in a constant volume gas thermometer at steam point (373.15K) is 1.50×104Pa. What will be the pressure of the triple point of water?
View SolutionA weather balloon has a volume of 175 L when filled with hydrogen at a pressure of 1.000 atm. Calculate the volume of the balloon when it rises to a height of 2000 m, where atmospheric pressure is 0.8000 atm. Assume that temperature is constant.
View SolutionA compressed cylinder of gas contains 1.50×103 g of N2 gas at a pressure of 2.0×107 Pa and a temperature of 17.1∘C. What volume of gas has been released into the atmosphere if the final pressure in the cylinder is 1.80×105 Pa ? Assume ideal behaviour and that the gas temperature is unchanged.
View SolutionWhat will be the volume occupied by 2 gm of hydrogen at 300 K and 4 atmospheric pressure if at 273 k and 1 atmospheric pressure the gas occupies 22.4 L.
View SolutionThe weight of CH4 in a 9L cylinder at 27∘C temperature and 16 atm pressure is (R = 0.08 L atm K−1mol−1 )
View SolutionA gas at 27∘C in a cylinder has a volume of 4 litre and pressure 100Nm−2.
(i) Gas is first compressed at constant temperature so that the pressure is 150Nm−2 . Calaulate the change in volume.
(ii) It is then heated at constant volume so that temperature becomes 127∘C. Calculate the new pressure.
View Solution

