A cube of mass 1 kg and volume is placed in an evacuated chamber at . Initially temperature of block is . Assume block behaves like a block body, find the rate of cooling of block if specific heat of the material of block is .
To solve the problem step by step, we will follow the outlined approach based on the information given in the question.
Step 1: Identify the given data
- Mass of the block, m=1kg
- Volume of the block, V=125cm3
- Initial temperature of the block, Ti=227°C
- Temperature of the chamber, T0=27°C
- Specific heat of the material, c=400J/kg⋅K
Step 2: Convert temperatures to Kelvin
To use the Stefan-Boltzmann law, we need to convert the temperatures from Celsius to Kelvin.
- Ti=227+273=500K
- T0=27+273=300K
Step 3: Calculate the side length of the cube
Using the volume of the cube:
V=a3⟹a=√(3)V=√(3)125cm3=5cm
Step 4: Calculate the surface area of the cube
The surface area A of a cube is given by:
A=6a2
Substituting the side length:
A=6×(5cm)2=6×25cm2=150cm2
Step 5: Convert the surface area to square meters
To use in calculations, convert A from cm2 to m2:
A=150cm2=150×10−4m2=0.015m2
Step 6: Apply the Stefan-Boltzmann law for rate of heat loss
The rate of heat loss dQdt is given by:
dQdt=σA(T4i−T40)
Where σ=5.67×10−8W/m2K4.
Substituting the values:
dQdt=5.67×10−8×0.015×(5004−3004)
Step 7: Calculate 5004 and 3004
Calculating the powers:
5004=62500000000and3004=8100000000
Thus,
5004−3004=62500000000−8100000000=54400000000
Step 8: Substitute back to find dQdt
dQdt=5.67×10−8×0.015×54400000000
Calculating this gives:
dQdt≈4.65W
Step 9: Relate heat loss to cooling rate
Using the relation:
dQdt=mcdTdt
Rearranging gives:
dTdt=1mcdQdt
Substituting m=1kg and c=400J/kg⋅K:
dTdt=11×400×4.65≈0.011625K/s
Step 10: Finalize the rate of cooling
Thus, the rate of cooling of the block is:
dTdt≈0.011625°C/s≈0.115°C/s
Final Answer
The rate of cooling of the block is approximately 0.115°C/s.
---
- Mass of the block, m=1kg
- Volume of the block, V=125cm3
- Initial temperature of the block, Ti=227°C
- Temperature of the chamber, T0=27°C
- Specific heat of the material, c=400J/kg⋅K
To use the Stefan-Boltzmann law, we need to convert the temperatures from Celsius to Kelvin.
- Ti=227+273=500K
- T0=27+273=300K
Using the volume of the cube:
V=a3⟹a=√(3)V=√(3)125cm3=5cm
The surface area A of a cube is given by:
A=6a2
Substituting the side length:
A=6×(5cm)2=6×25cm2=150cm2
To use in calculations, convert A from cm2 to m2:
A=150cm2=150×10−4m2=0.015m2
The rate of heat loss dQdt is given by:
dQdt=σA(T4i−T40)
Where σ=5.67×10−8W/m2K4.
dQdt=5.67×10−8×0.015×(5004−3004)
Calculating the powers:
5004=62500000000and3004=8100000000
Thus,
5004−3004=62500000000−8100000000=54400000000
dQdt=5.67×10−8×0.015×54400000000
Calculating this gives:
dQdt≈4.65W
Using the relation:
dQdt=mcdTdt
Rearranging gives:
dTdt=1mcdQdt
Substituting m=1kg and c=400J/kg⋅K:
dTdt=11×400×4.65≈0.011625K/s
Thus, the rate of cooling of the block is:
dTdt≈0.011625°C/s≈0.115°C/s
The rate of cooling of the block is approximately 0.115°C/s.
Topper's Solved these Questions
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Single Correct
Explore 148 Videos
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Multiple Correct
Explore 25 Videos
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Exercise 1.3
Explore 18 Videos
- BASIC MATHEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:BASIC MATHEMATICSExercise:Exercise 2.6
Explore 20 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
A cubical block of mass 1.0kg and edge 5.0cm is heated to 227∘C . It is kept in an evacuated chamber maintained at 27∘C . Assming that the block emits radiation like a blackbody, find the rate at which the temperature of the block will decreases. Specific heat capacity of the material of the block is 400Jkg−1K−1 .
View SolutionA cubical block of mass 1.0kg and edge 5.0cm is heated to 227∘C . It is kept in an evacuated chamber maintained at 27∘C . Assming that the block emits radiation like a blackbody, find the rate at which the temperature of the block will decreases. Specific heat capacity of the material of the block is 400Jkg−1K−1 .
View SolutionTwo blocks of masses 1 kg and 2 kg are placed in contact on a smooth horizontal surface as shown in fig. A horizontal force of 6N is applied d(a) on a 1-kg block. Find the force of interaction of the blocks.

 .
.
View SolutionA metal block is placed in a room which is at 10∘C for long time. Now it is heated by an electric heater of power 500 W till its temperature becomes 50∘C. Its initial rate of rise of temperature is 2.5∘C/sec. The heater is switched off and now a heater of 100W is required to maintain the temperature of the block at 50∘C . (Assume Newtons Law of cooling to be valid)
What is the rate of cooling of block at 50∘C if the 100W heater is also switched off?
View SolutionA block of mass 1 kg is placed on a horizontal surface . The reaction force to the weight of the block is
View SolutionIn the figure shown, block of mass 2 kg is very long. Force of friction on 1 kg block is
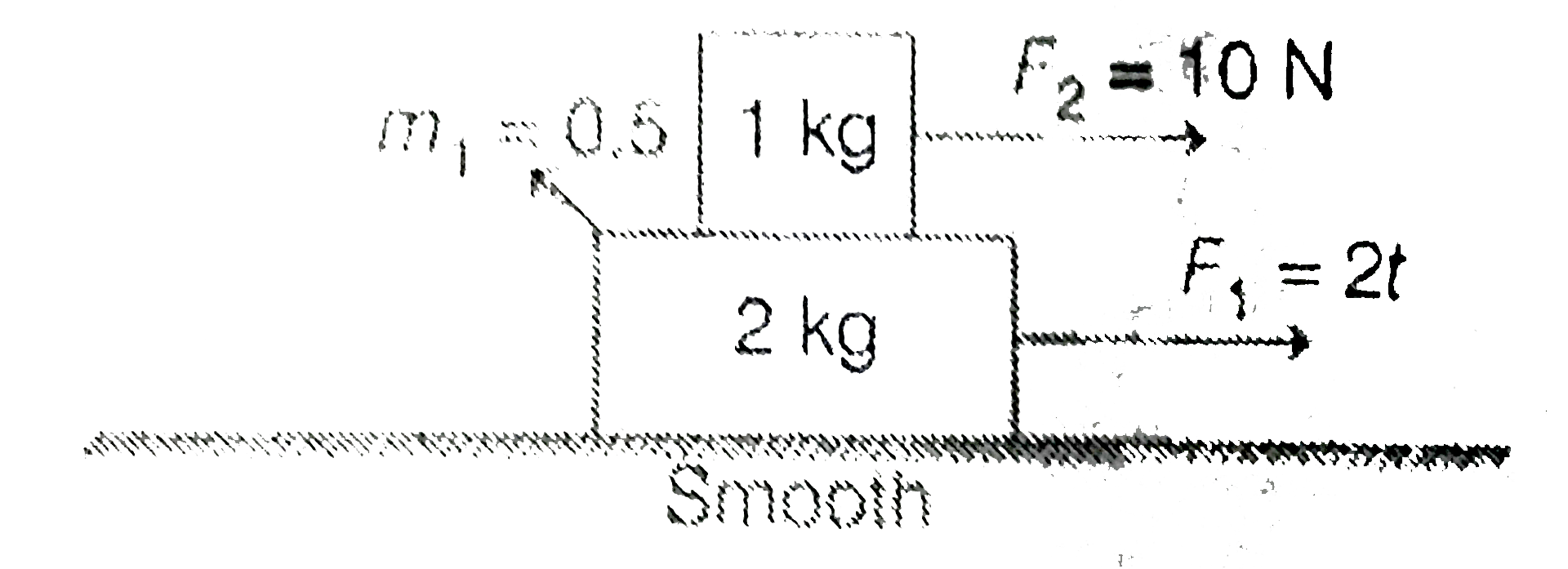
View SolutionA copper block of mass 60kg is heated till its temperature is increased by 20∘C . Find the heat supplied to the block. Specific heat capacity of =0.09calg−1−C.
View SolutionA block of mass 5 kg is at rest on a smooth horizontal surface. Water coming out of a pipe horizontally at the rate of 2 kgs−1 , hits the block with a velocity of 6ms−1.The initial acceleration of the block is,
View SolutionA copper block of mass 2.5kg is heated in a furnace to a temperature of 500∘C and then placed on a large ice block. What is the maximum amount (approx.) of ice that can melt? (Specific heat copper =0.39J/g∘C heat of fusion of water =335J/g).
View SolutionIn the following arrangement, the system is initially at rest. The 5-kg block is now released. Assuming the pulley and string to be massless and smooth, the acceleration of block C will be
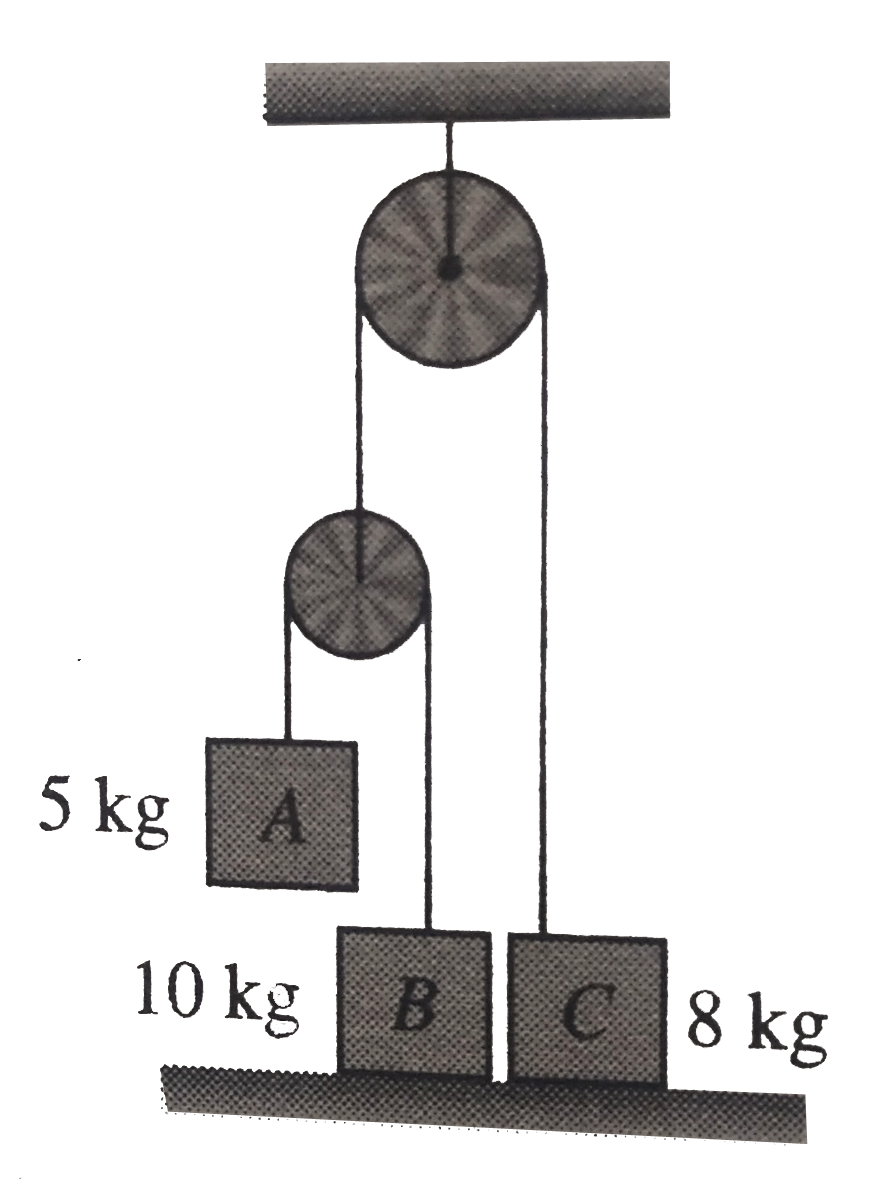
View Solution