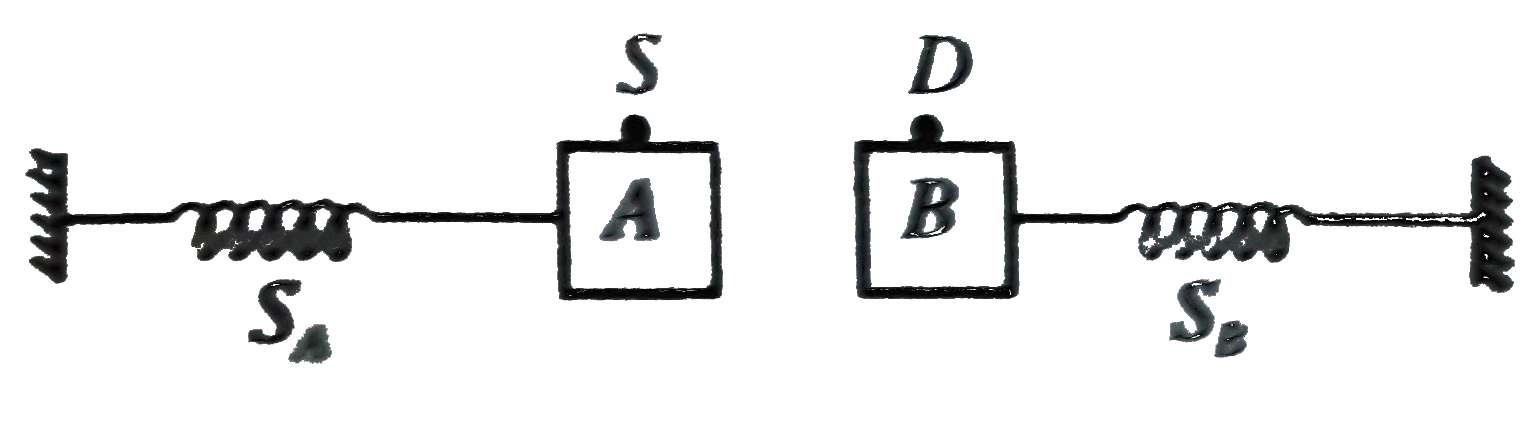
A source S emitting sound of 300 Hz is fixed of block A which is attached to free end of a spring SA as shown in the figure. The detector D fixed on block B attached to the free end of spring SB detects this sound.
The blocks A and B are simultaneously displaced towards each other through of 1.0 m and then left to vibrate. Find the maximum and minimum frequencies of sound detected by D if the vibrational frequency of each block is 2 Hz (velocity of sound is 340 m/s).
The motion of A and B is sychronized. Hence the maximum frequencies detected by D will be
fmax=(v+vDv−vS)f
(when S and D are approaching each other while at their equilibrium position.)
=(340+Aω340−Aω)f=(340+12.56340−12.56)×300=323Hz
Similarly, the apparent frequency will be minimum when the source and the detector recede from each other with maximum speed (=Aω)
fmin=(v−Aωv+Aω)f=(340−12.56340+12.56)×300=278.6Hz
Topper's Solved these Questions
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Exercise 6.1
56 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Exercise 6.2
72 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type
5 Videos
Similar Questions
A source S emitting sound of 300Hz is fixed on block A which is attache to free end of a spring SA as shown in figure. The detector D fixed on block B attached to free end of spring SB detects this sound. The blocks A and B simultaneously displaced towards each other thrugh a distance of 2.0m and then left to vibrate. If the product of maximum and minimum freuquencies of sound detected by D is K+104sec−2. Find K. Given the vibrational frequencies of each block is 5/πHz. speed of sound in air =300m/s
View SolutionA blocked of mass m is attached with two strings as shown in figure .Draw the free body diagram of the block.

View SolutionA block of mass m is attached with two strings as shown in figure .Draw the free body diagram of the block.

View SolutionBlock 'A' is placed ober the block 'B' as shown in the figure. Wedge is fixed and there is no friction. Between block 'B' and fixed inclined. Force of friction on the block 'A' is
View Solution
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will be
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

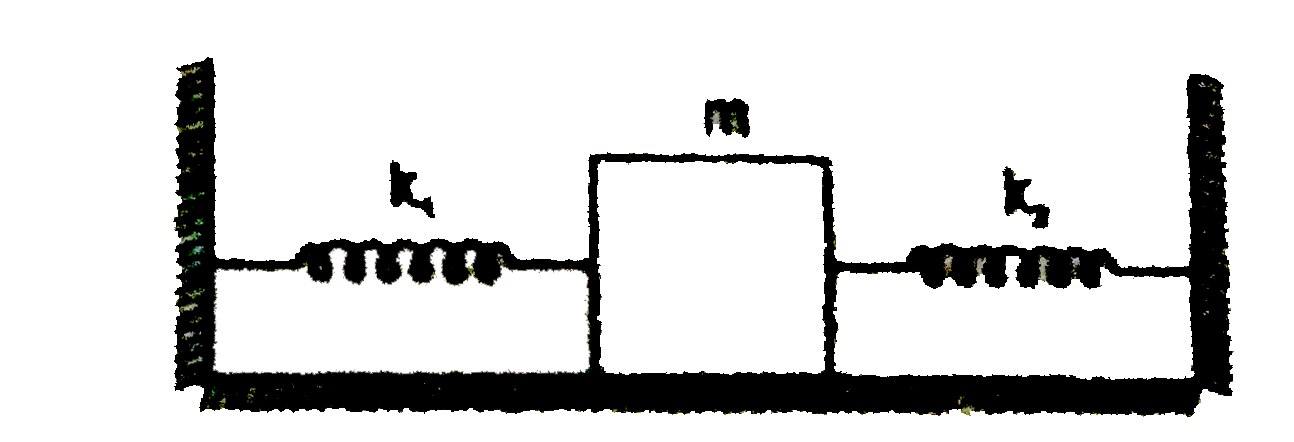
View SolutionA block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it passes through the mean position shown.

View SolutionTwo springs are in a series combination and are attached to a block of mass 'm' which is in equilibrium. The spring constants and extension in the springs are as shown in the figure. Then the force exerted by the spring on the block is :
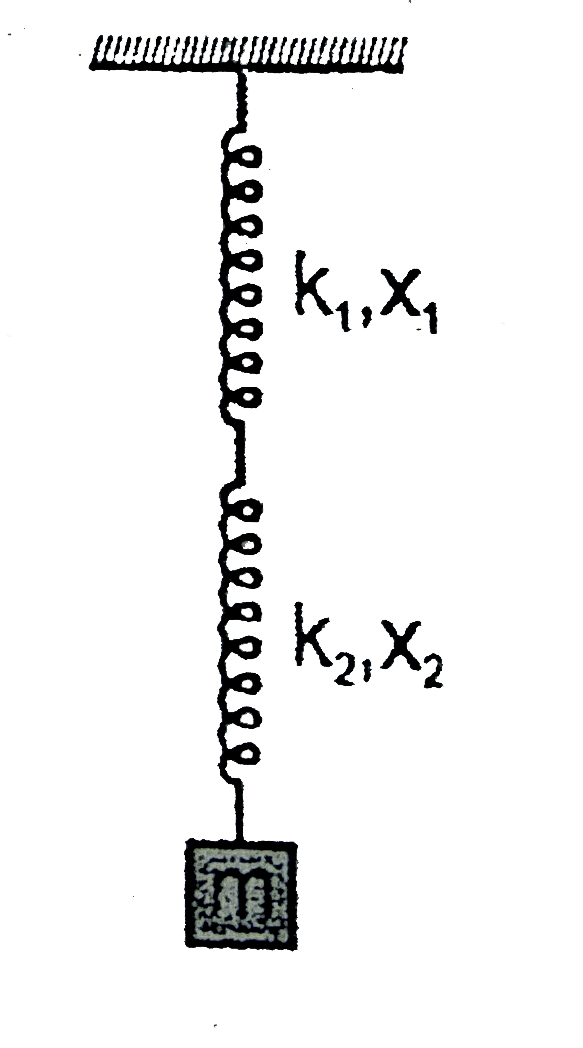
View SolutionA block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is
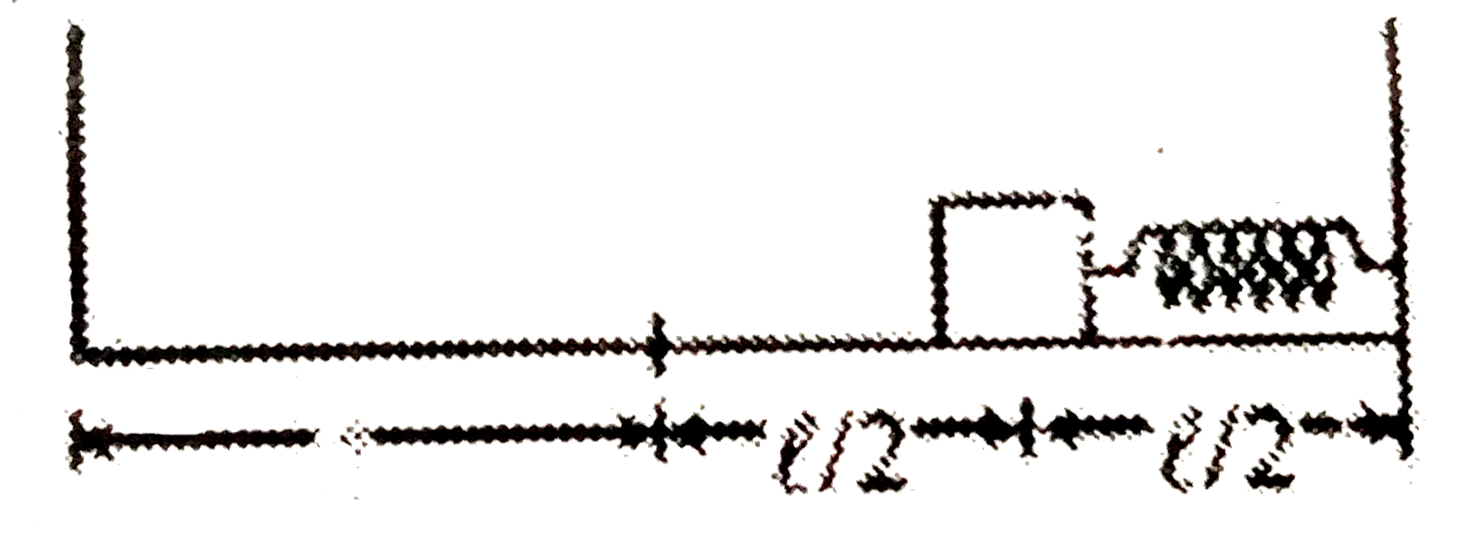
View SolutionA block of mass m is attached to two unstretched springs of springs constant k1 and k2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it passes through the mean position shown.
View Solution
