An observer standing on a railway crossing receives frequencies 2.2 kHz and 1.8 kHz when the tran approaches and recedes from the observer. Find the velocity of the train (speed of sound in air is 300 m/s).
To solve the problem of finding the velocity of the train based on the frequencies received by the observer, we can follow these steps:
Step 1: Understand the Doppler Effect
When a source of sound (the train) moves towards an observer, the frequency heard by the observer increases. Conversely, when the source moves away, the frequency decreases. This phenomenon is known as the Doppler Effect.
Step 2: Set Up the Equations
Let:
- f1 = frequency heard when the train approaches = 2.2 kHz = 2200 Hz
- f2 = frequency heard when the train recedes = 1.8 kHz = 1800 Hz
- v = speed of sound in air = 300 m/s
- vs = speed of the train (what we need to find)
Using the Doppler Effect formulas:
- When the train approaches:
f1=vv−vsf
- When the train recedes:
f2=vv+vsf
Step 3: Set Up the Ratio of Frequencies
We can take the ratio of the two frequencies:
f1f2=v+vsv−vs
Substituting the known frequencies:
22001800=v+vsv−vs
This simplifies to:
119=v+vsv−vs
Step 4: Cross Multiply
Cross multiplying gives us:
11(v−vs)=9(v+vs)
Expanding both sides:
11v−11vs=9v+9vs
Step 5: Rearranging the Equation
Rearranging the equation to isolate vs:
11v−9v=11vs+9vs
This simplifies to:
2v=20vs
Step 6: Solve for vs
Now, we can solve for vs:
vs=2v20=v10
Substituting the value of v:
vs=30010=30 m/s
Final Answer
The velocity of the train is 30 m/s.
---
When a source of sound (the train) moves towards an observer, the frequency heard by the observer increases. Conversely, when the source moves away, the frequency decreases. This phenomenon is known as the Doppler Effect.
Let:
- f1 = frequency heard when the train approaches = 2.2 kHz = 2200 Hz
- f2 = frequency heard when the train recedes = 1.8 kHz = 1800 Hz
- v = speed of sound in air = 300 m/s
- vs = speed of the train (what we need to find)
- When the train approaches:
f1=vv−vsf
- When the train recedes:
f2=vv+vsf
We can take the ratio of the two frequencies:
f1f2=v+vsv−vs
Substituting the known frequencies:
22001800=v+vsv−vs
This simplifies to:
119=v+vsv−vs
Cross multiplying gives us:
11(v−vs)=9(v+vs)
Expanding both sides:
11v−11vs=9v+9vs
Rearranging the equation to isolate vs:
11v−9v=11vs+9vs
This simplifies to:
2v=20vs
Now, we can solve for vs:
vs=2v20=v10
Substituting the value of v:
vs=30010=30 m/s
The velocity of the train is 30 m/s.
Topper's Solved these Questions
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Exercise 6.1
56 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Exercise 6.2
72 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type
5 Videos
Similar Questions
A whistling train approaches a junction. An observer standing at juction observes the frequency to be 2.2KHz and 1.8KHz of the approaching and the receding train respectively. Find the speed of the train (speed of sound 300m/s)
View SolutionThe ratio of the apparent frequencies of a car when approaching and receding a stationary observer is 11:9 What is the speed of the car, if the velocity of sound in air is 330 m/s?
View SolutionA fighter plane moving in a vertical loop with constant speed of radius R . The center of the loop is as a height h directly overhead of an observer standing on the ground. The observer receives maximum frequency of the sound produced by the plane when it is nearest to him . Find the speed of the plane. Velocity of sound in air is υ .
View SolutionA man standing 25 m away from a wall produces a sound and receives the reflected sound.
Calculate the time after which he receives the reflected sound if the speed of sound in air is 350 m s−1.
View SolutionThe frequency of the whistle of a train is observed to drop from 280 Hz to 260 Hz as the train moves away from a stationary listerner on the platform. Calculate the speed of the train, if speed of sound in air is 340 m/s.
View SolutionA car moving at a speed of 72km/hr sounds its whistle which has a frequency of 550Hz, Find the frequencies heard by a stationary observer as the car approaches and then recedes from the observer, velocity of sound =340m/s.
View SolutionAn engine giving off whistle is moving towards a stationary observer with 50m/s speed. What will be the ratio of the frequencies of the whistle heard when engine is approaching and receding from the observer? (speed of sound = 350 m/s)
View SolutionA source of sound attached to the bob of a simple pendulum execute SHM . The difference between the apparent frequency of sound as received by an observer during its approach and recession at the mean frequency of the source . The velocity of the source at the mean position is ( velocity of sound in the air is 340m/s)
[Assume velocity of sound << velocity of sound in air ]
View Solution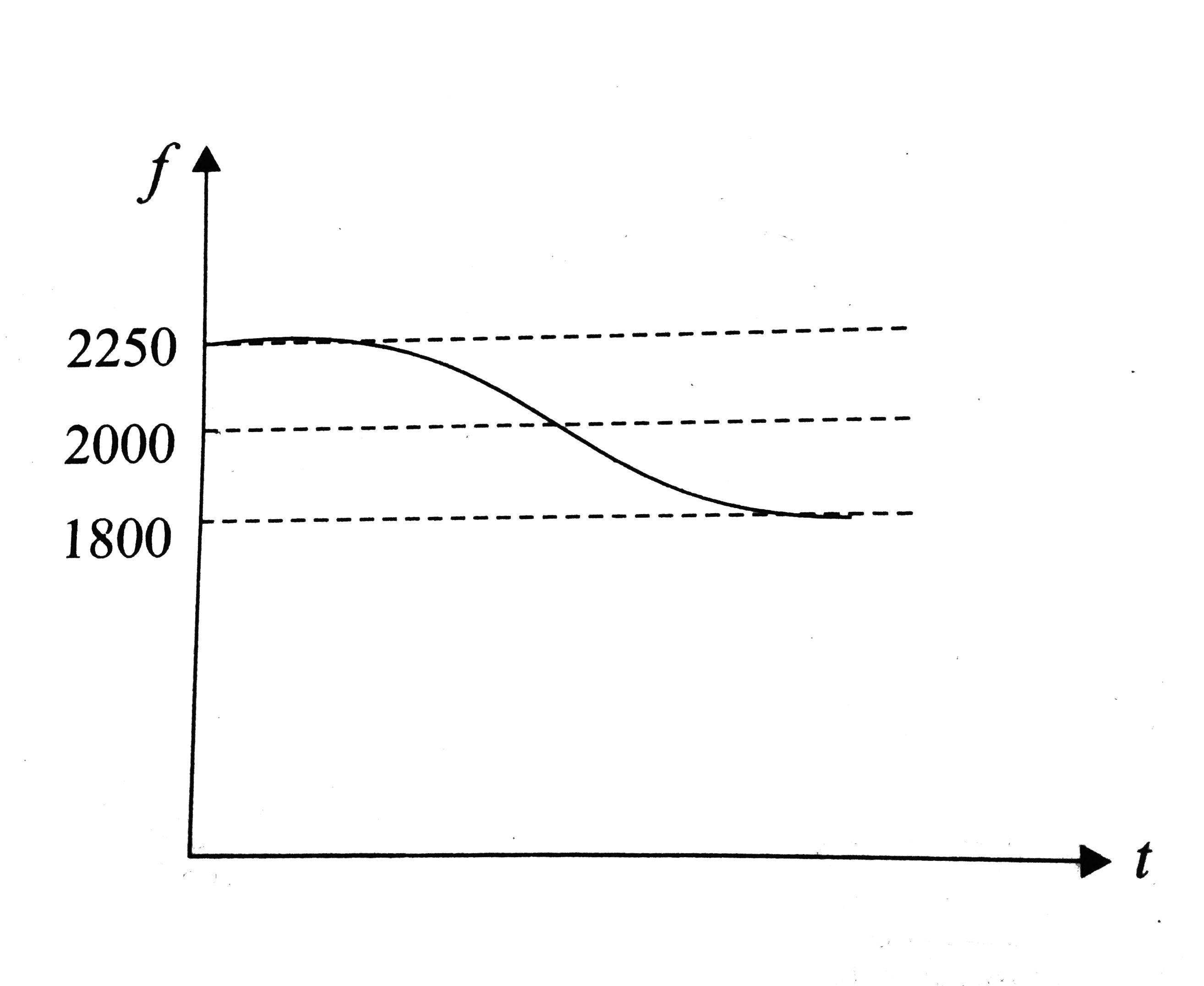
A statinary observer receives a sound of frequency 2000 Hz. The variation of apparent frequency and time is shown. Find the speed of source, if velocity of sound is 300ms
View SolutionA stationary source of sound is emitting sound of frequency 500Hz. Two observers A and B lying on the same line as the source, observe frequencies 480Hz and 530Hz respectively. The velocity of A and B respectively are (in m/s), speed of sound =300m/s.
View Solution
