In the previous problem, the maximum range of movement of the centre of the part of the circle from line AD in which charged particle of charge Q moves with a velocity v when (θ) is positive to when (θ) is negative is given by
±mv2QB
±mvQB
±2mvQB
±2mv3QB
The correct Answer is:B
To solve the problem of finding the maximum range of movement of the center of the path of a charged particle in a magnetic field, we can follow these steps:
1. Understanding the Motion:
The charged particle of charge Q moves with a velocity v in a magnetic field. The motion of the charged particle will be circular due to the Lorentz force acting on it.
2. Identifying the Angle:
The problem states that we are considering the angles θ as positive and negative. When θ is positive, it indicates one direction of motion, and when θ is negative, it indicates the opposite direction.
3. Determining the Radius of Circular Motion:
The radius r of the circular path traced by the charged particle in a magnetic field is given by the formula:
r=mvQB
where:
- m is the mass of the particle,
- v is the velocity of the particle,
- Q is the charge of the particle,
- B is the magnetic field strength.
4. Calculating Maximum Distance:
When the angle θ is +90∘, the center of the circular path will be at a distance r from the line AD. Conversely, when θ is −90∘, the center will also be at a distance r but in the opposite direction. Therefore, the maximum range of movement of the center from line AD can be expressed as:
Maximum Range=r (positive direction)+r (negative direction)=r+(−r)=2r
5. Final Expression:
Substituting the expression for r:
Maximum Range=2(mvQB)
Conclusion:
Thus, the maximum range of movement of the center of the part of the circle from line AD is given by:
Maximum Range=2mvQB
The charged particle of charge Q moves with a velocity v in a magnetic field. The motion of the charged particle will be circular due to the Lorentz force acting on it.
The problem states that we are considering the angles θ as positive and negative. When θ is positive, it indicates one direction of motion, and when θ is negative, it indicates the opposite direction.
The radius r of the circular path traced by the charged particle in a magnetic field is given by the formula:
r=mvQB
where:
- m is the mass of the particle,
- v is the velocity of the particle,
- Q is the charge of the particle,
- B is the magnetic field strength.
When the angle θ is +90∘, the center of the circular path will be at a distance r from the line AD. Conversely, when θ is −90∘, the center will also be at a distance r but in the opposite direction. Therefore, the maximum range of movement of the center from line AD can be expressed as:
Maximum Range=r (positive direction)+r (negative direction)=r+(−r)=2r
Substituting the expression for r:
Maximum Range=2(mvQB)
Thus, the maximum range of movement of the center of the part of the circle from line AD is given by:
Maximum Range=2mvQB
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct
34 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Linked Comprehension
84 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.5
14 Videos
Similar Questions
In the previous problem, if time period, T=2(π)mBQ where Q is the charge of the particle and m is its mass, the ratio of time spent by the particle in field when (θ) is positive to when (θ) is negative is given by
View SolutionWhat is the direction of the force acting on a charged particle q, moving with a velocity →v a uniform magnetic field →B ?
View SolutionA positive charged particle when moves from higher potential to lower potential
View SolutionA charged particle (charge q) is moving in a circle of radius R with unifrom speed v. The associated magnetic moment μ is given by
View SolutionTo the right of line PQ is a uniform magnetic field →B.B1A is the line of incidence of a charged particle, which comes out of the field along DE, CA and DF are the normals at A and D. −B1AC=(θ). Angle measured from CA in clockwise direction is taken as positive. What will be the value of (θ) so that angle subtended by the part of the circle (along which charged particle moves in the field) at its centre and facing the circle is less than π?
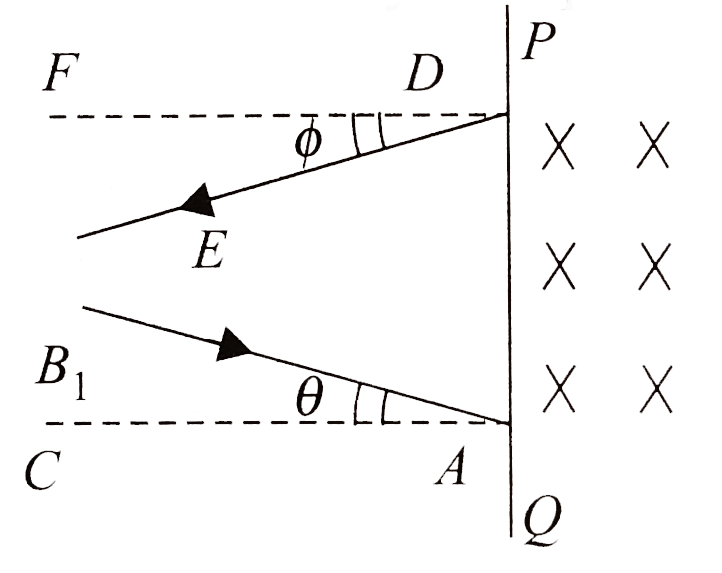
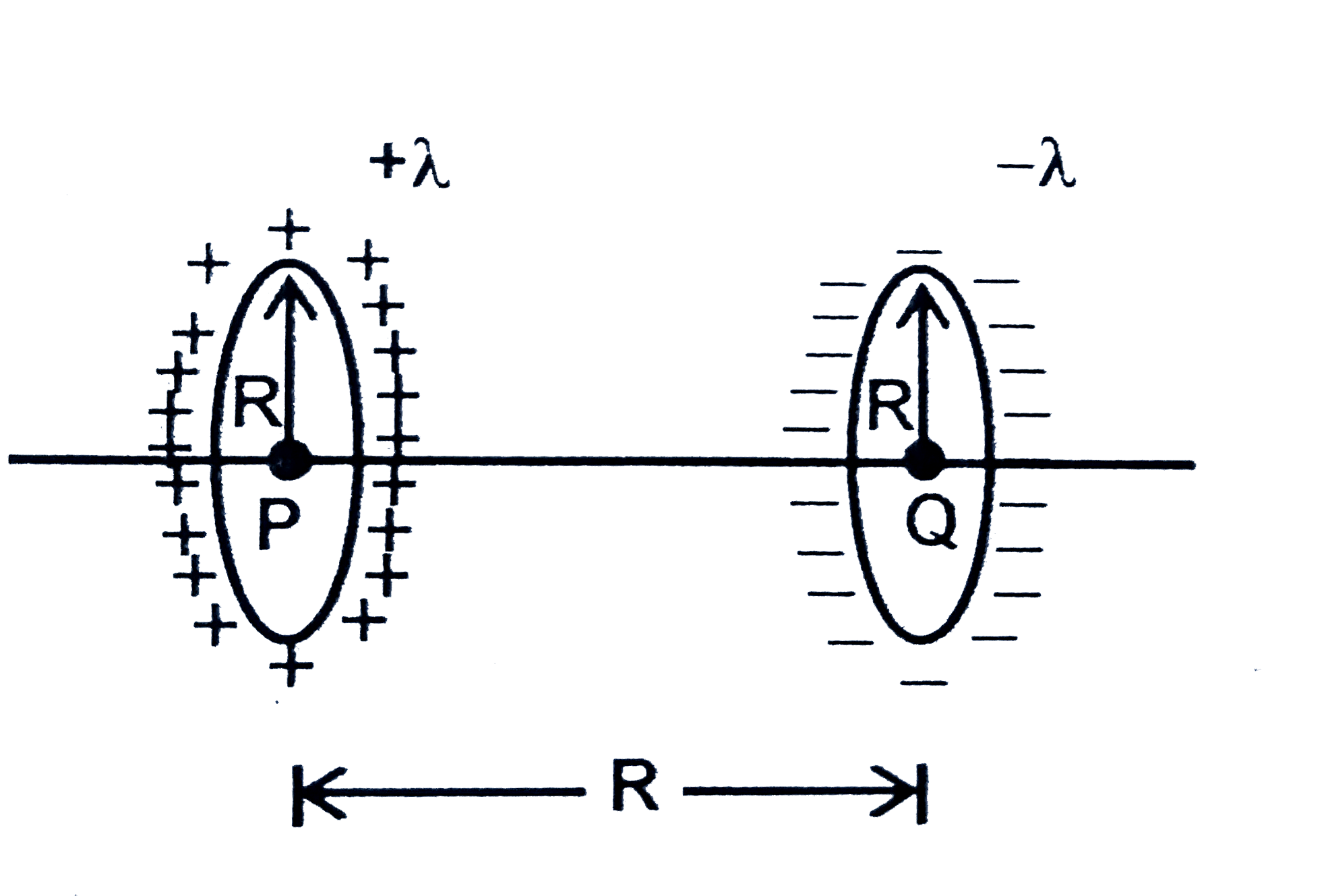
View SolutionTwo fixed insulating rings A and B carry ahanges with uniform linear aharge density +λ and −λ, respectively, as shown in the adjacent figure. The planes of the rings are parallel to each other and their axes are coinciding. A particle of change "q" and mass "m" is released with zero velocity from centre P of the positively charged ring. The kinetic energy of the particle when it reaches centre Q of the negatively charge ring will be
View SolutionWhen a charged particle moves in an elecltric or a magnetic field, its speed is v and acceleration is a
View SolutionA particle of charge q is projected from point P with velocity v as shown. Choose the correct statement from the following.

View SolutionWrite the expression for the de-Broglie wavelength associated with a charged particle having charge 'q' and mass 'm' when it is accelerated by a potential V.
View SolutionThe change in the kinetic energy of a charged particle moving in a uniform magnetic field will be zero when its velocity is
View Solution
