In a region at a distance r from z-axis, magnetic field →B=B0rtˆk is present where B0 is constant and t is time. Then the magnetic of induced electric field at a distance r from z-axis is given by
r2B0
r22B0
r23B0
none
The correct Answer is:C
To solve the problem of finding the induced electric field at a distance r from the z-axis due to a time-varying magnetic field, we can follow these steps:
Step 1: Understand the Given Magnetic Field
The magnetic field is given by:
→B=B0Rt^k
where B0 is a constant, R is the radial distance from the z-axis, and t is time.
Step 2: Calculate the Magnetic Flux
The magnetic flux Φ through a circular area of radius r is given by:
Φ=∫→B⋅d→A
where d→A is the differential area vector. For a circular area in the plane perpendicular to the z-axis, d→A=dA^k and dA=2πrdr.
Substituting →B and dA:
Φ=∫B0Rt^k⋅(2πrdr^k)=∫B0Rt(2πr)dr
This simplifies to:
Φ=B0Rt⋅2π∫rdr
Step 3: Integrate to Find the Flux
Now, we need to integrate:
∫rdr=r22
Thus, the flux becomes:
Φ=B0Rt⋅2π(r22)=πB0Rtr2
Step 4: Differentiate the Flux with Respect to Time
To find the induced electric field, we need to differentiate the flux with respect to time t:
dΦdt=πB0Rr2ddt(t)=πB0Rr2
Step 5: Use Faraday's Law of Induction
According to Faraday's law, the induced electromotive force (emf) is given by:
E=−dΦdt
Thus:
E=−πB0Rr2
Step 6: Relate emf to the Electric Field
The induced emf can also be expressed as:
E=∮→E⋅d→L
For a circular path of radius r, this becomes:
E=E⋅(2πr)
Step 7: Set the Two Expressions for emf Equal
Equating the two expressions for emf:
E⋅(2πr)=−πB0Rr2
Step 8: Solve for the Electric Field E
Dividing both sides by 2πr:
E=−B0Rr22r=−B0Rr2
Final Result
The induced electric field at a distance r from the z-axis is:
E=B0Rr2
The magnetic field is given by:
→B=B0Rt^k
where B0 is a constant, R is the radial distance from the z-axis, and t is time.
The magnetic flux Φ through a circular area of radius r is given by:
Φ=∫→B⋅d→A
where d→A is the differential area vector. For a circular area in the plane perpendicular to the z-axis, d→A=dA^k and dA=2πrdr.
Φ=∫B0Rt^k⋅(2πrdr^k)=∫B0Rt(2πr)dr
This simplifies to:
Φ=B0Rt⋅2π∫rdr
Now, we need to integrate:
∫rdr=r22
Thus, the flux becomes:
Φ=B0Rt⋅2π(r22)=πB0Rtr2
To find the induced electric field, we need to differentiate the flux with respect to time t:
dΦdt=πB0Rr2ddt(t)=πB0Rr2
According to Faraday's law, the induced electromotive force (emf) is given by:
E=−dΦdt
Thus:
E=−πB0Rr2
The induced emf can also be expressed as:
E=∮→E⋅d→L
For a circular path of radius r, this becomes:
E=E⋅(2πr)
Equating the two expressions for emf:
E⋅(2πr)=−πB0Rr2
Dividing both sides by 2πr:
E=−B0Rr22r=−B0Rr2
The induced electric field at a distance r from the z-axis is:
E=B0Rr2
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct
34 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Linked Comprehension
84 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.5
14 Videos
Similar Questions
A cylindrical space of radius R is filled with a uniform magnetic induction parallel to the axis of the cylinder. If B charges at a constant rate, the graph showin the variation of induced electric field with distance r from the axis of cylinder is
View SolutionFigure shows a circular region of radius R in which uniform magnetic field B exists. The magnetic field is increasing at a rate dBdt. The induced electric field at a distance r from the centre for r<R is

View SolutionA uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region

View SolutionA uniform but time varying magnetic field B(t) exist in a circular region of radius a and is directed into the plane of the paper as shown. The magnitude of the induced electric field at point P at a distance r form the centre of the circular region.

View SolutionSuppose that the current density in a wire of radius a varius with r according to Kr2 where K is a constant and r is the distance from the axis of the wire. Find the magnetic field at a point at distance r form the axis when (a) r<a and (b) r>a.
View SolutionIn region x>0 a uniform and constant magnetic field →B1=2B0ˆk exists. Another uniform and constant magnetic field →B2=B0ˆk exists in region x<0 A positively charged particle of mass m and charge q is crossing origin at time t =0 with a velocity ¯u=u0ˆi. The particle comes back to its initial position after a time : (B0,u0 are positive constants)
View SolutionCurrent flows through a straight, thin-walled tube of radius r. The magnetic field at a distance x from the axis of the tube has magnitude B.
View SolutionThe magnetic field on the axis at a distance z from the centre of the bar magnet would be ?
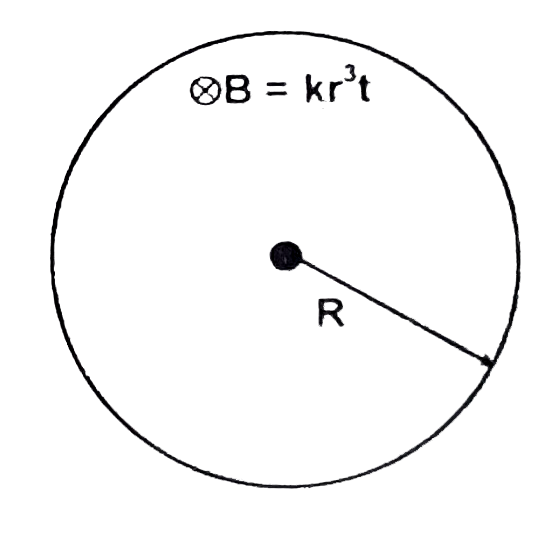
View SolutionA time varying magnetic field B=Kr3t is existing in a cylindrical region of radius 'R' as shown (where k is a constant). The induced electric field 'E' at rR2 is
View SolutionA magnetic field →B=B0ˆj , exists in the region a<x<2a , and →B=−B0ˆj , in the region 2a<x<3a, where B0 is a positive constant . A positive point charge moving with a velocity →v=v0ˆi , where v0 is a positive constant , enters the magnetic field at x=a . The trajectory of the charge in this region can be like

View Solution
