Axis of a solid cylinder of infinite length and radius R lies along y-axis. It carries a uniformly distributed current I along +y direction. Magnetic field at a point (R/2,y,R/2) is
μ0I4πR(ˆi−ˆk)
μ0I2πR(ˆj−ˆk)
μ0I4πRˆj
μ0I4πR(ˆi+ˆk)
The correct Answer is:A
r=R√2,(B)=μ0I(R/√2)2πR2=μ0I2√2πR
→B=B[cos45∘ˆi+sin45∘(kˆk)]=μ0I4πR[ˆi−ˆk]

Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct
34 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Linked Comprehension
84 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.5
14 Videos
Similar Questions
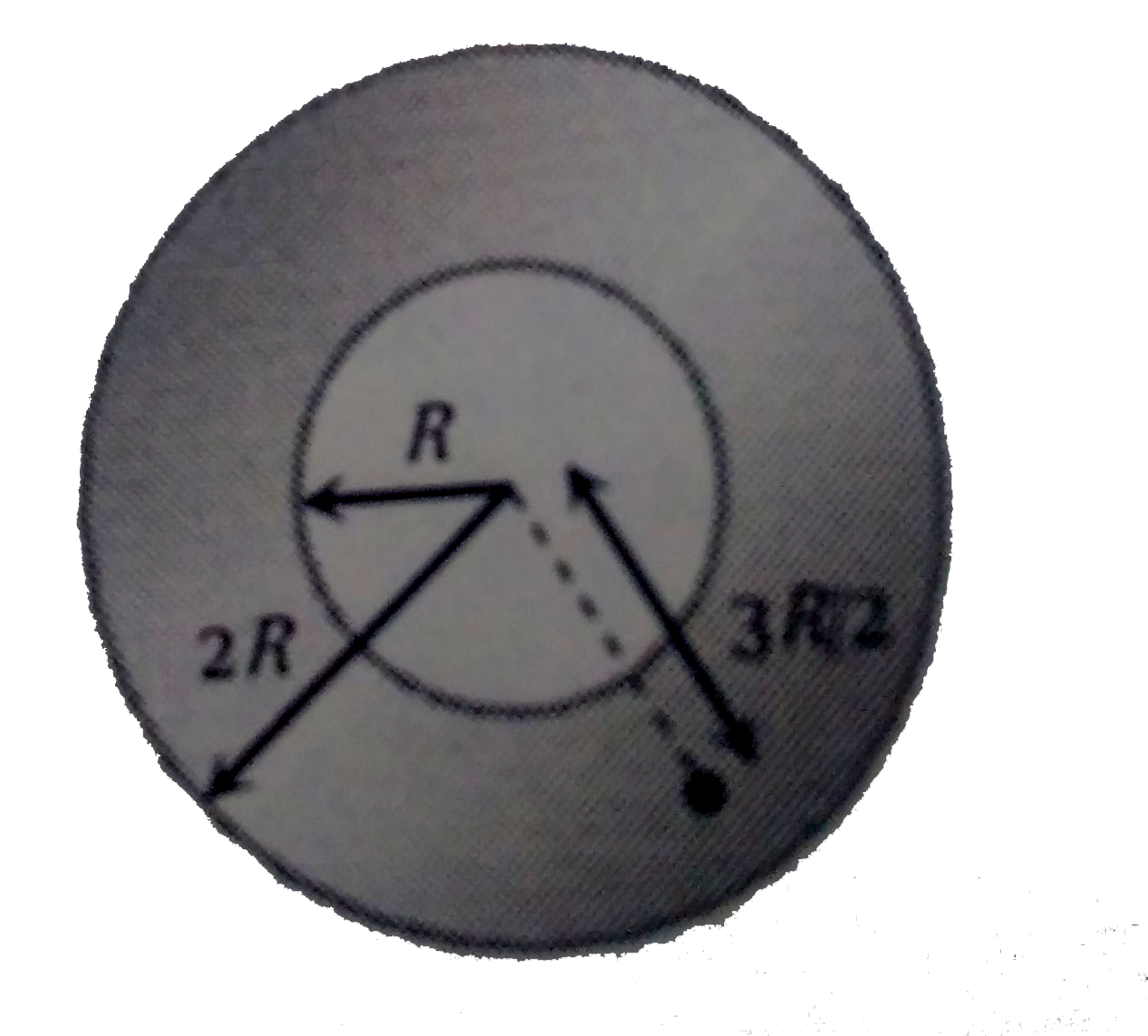
Figure shows the cross-sectional view of the hollow cylindrical conductor with inner radius 'R' and outer radius '2R', cylinder carrying uniformly distributed current along it's axis. The magnetic induction at point 'P' at a distance 3R2 from the axis of the cylinder will be
View SolutionA long thick conducting cylinder of radius 'R' carries a current uniformly distributed over its cross section :
View SolutionStatement 1: A direct uniformly distributed current flows through a solid long metallic cylinder along its length. It produces magnetic field only outside the cylinder.
Statement 2: A thin long cylindrical tube carrying uniformly distributed current along its length does not produce a magnetic field inside it. Moreover, a solid cylinder can be supposed to be made up of many thin cylinderical tubes.
View SolutionCalculate potential on the axis of a ring due to charge Q uniformly distributed along the ring of radius R.
View SolutionA long straight conducting solid cylindrical wire of radius R carries a steady current / that is uniformly distributed throughout the cross section of the wire. Draw graph of magnetic field B versus r (where r is distance from the axis of the wire)
View SolutionSame current i is flowing in the three infinitely long wires along positive x-,y- and z-directions. The magnetic filed at a point (0,0,-a) would be
View SolutionA long, straight wire of radius R carries a current distributed uniformly over its cross section. The magnitude of the magnetic field is
View SolutionConsider a system of two long coaxial cylinders: solid (of radius a carrying i current in positive z direction) and hollow (or radius b carrying current i in negative z direction). Find the magnetic field at a point distant r from of the cylinders for
(i) r≤a
(ii) a<r<b
(iii) r>b

View SolutionA long wire in the shape of a cylindrical shell of inner and outer radii R2 and R respectively carries a steady current I in a direction parallel to its length. This current is uniformly distributed across the area of cross-section of the wire. The magnetic field intensity at a point at a distance 3R4 from the axis of the wire is m(μ0IπR).. The value of m is _________.
View SolutionAn infinitely long hollow conducting cylinder with inner radius R2 and outer radius R carries a uniform current density along its length . The magnitude of the magnetic field , ∣∣→B∣∣ as a function of the radial distance r from the axis is best represented by
View Solution
