Consider a system of two long coaxial cylinders: solid (of radius a carrying i current in positive z direction) and hollow (or radius b carrying current i in negative z direction). Find the magnetic field at a point distant r from of the cylinders for
(i) r≤a
(ii) a<r<b
(iii) r>b

(i) For r≤a, magnetic field in only due to solid cylinder. Thus it is, B=μ0ir2πa2
(ii) For a<r<b, magnetic field is only due to solid cylinder Thus, B=μ0i2πr
(iii) For r≥b, magnetic field is due to both solid and hollow cylinders Thus,
B1=μ0i2πr, due to solid cylinder
B2=μ0i2πr, due to hollow cylinder
Also B1andB2 are in opposite directions
⇒NetB=B1−B2=0
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Illustration
14 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Try Yourself
27 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
A long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
View SolutionA long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
View SolutionA circular loop of radius r carries a current i. where should a long , straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the centre becomes zero?
View SolutionA long wire having a semi-circular loop of radius r carries a current I, as shown in Fig. Find the magnetic field due to entire wire.

View SolutionA circular loop of radius r carries a current i. How should a long, straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the center becomes zero?
View SolutionThe figure shows the cross section of two long coaxial tubes carrying equal current I in opposites directions. If B1 and B2 are magnetic fields at point 1 and 2 as shown in figure then
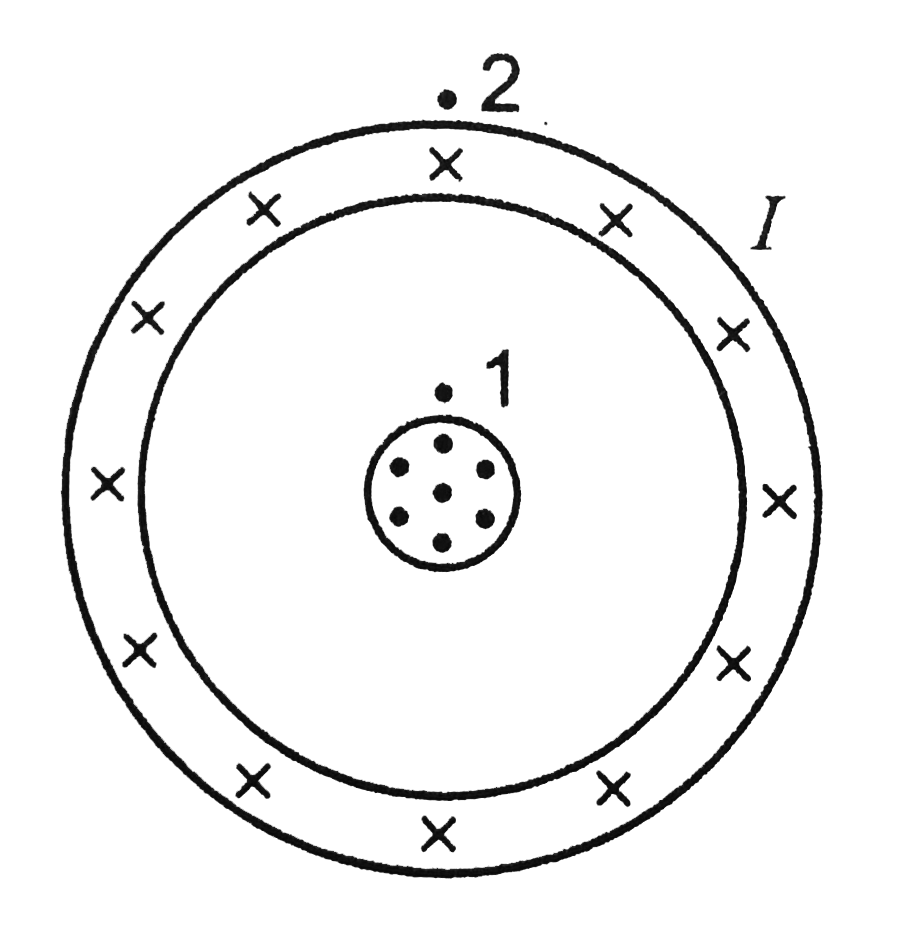
View SolutionA circular coil of radius 2R is carrying current 'i' . The ratio of magnetic fields at the centre of the coil and at a point at a distance 6R from the centre of the coil on the axis of the coil is
View SolutionFigure shown a section through two long thin concentric cylinders of radii a & b with a>b. The cylinders have equal and opposite per unit length λ. Find the electric field at a distance r from the axis for (i) r<a (ii) a<r<b (iii) r>b

View SolutionA long copper tube of inner radius R carriers a current i. The magnetic field B inside the tube is
View SolutionTwo long straight wires, each carrying a current I in opposite directions are separated by a distance R. The magnetic induction at a point mid way between the wire is
View Solution
