A cylindrical cavity of diameter a exists inside a cylinder of diameter 2a as shown in the figure. Both the cylinder and the cavity are infinitity long. A uniform current density j flows along the length . If the magnitude of the magnetic field at the point P is given by N12μ0Ja, then the value of N is
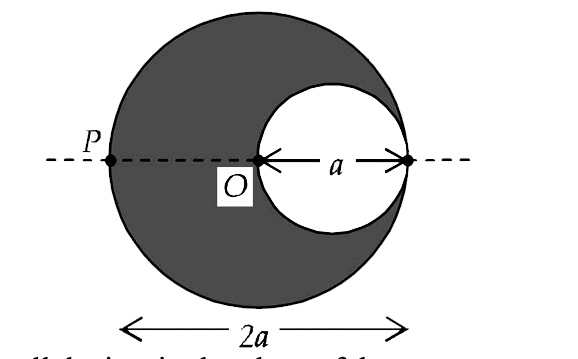
The correct Answer is:(5)
(5) B1=μJπa22πa=μ0Ja2,B2=μJπ(a/2)22π(3a/2)=μ0Ja12
B1−B2=μJa2−μJa12
=(μ0Ja2)(1−16)=56(μ0Ja2)=5μ0aJ12
=N12μ0aJ
∴N=5
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Subjective type
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Answer Type
35 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Archives (linked Comprehension)
4 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
A cylinderical cavity of diameter a exists inside a cylinder of diameter 2a as shown in the figure. Both the cylinder and the cavity are infinitely long. A uniform current density J flows along the length. If the magnitude of the magnetic field at the point P is given by N12μ0aJ, then the value of N is
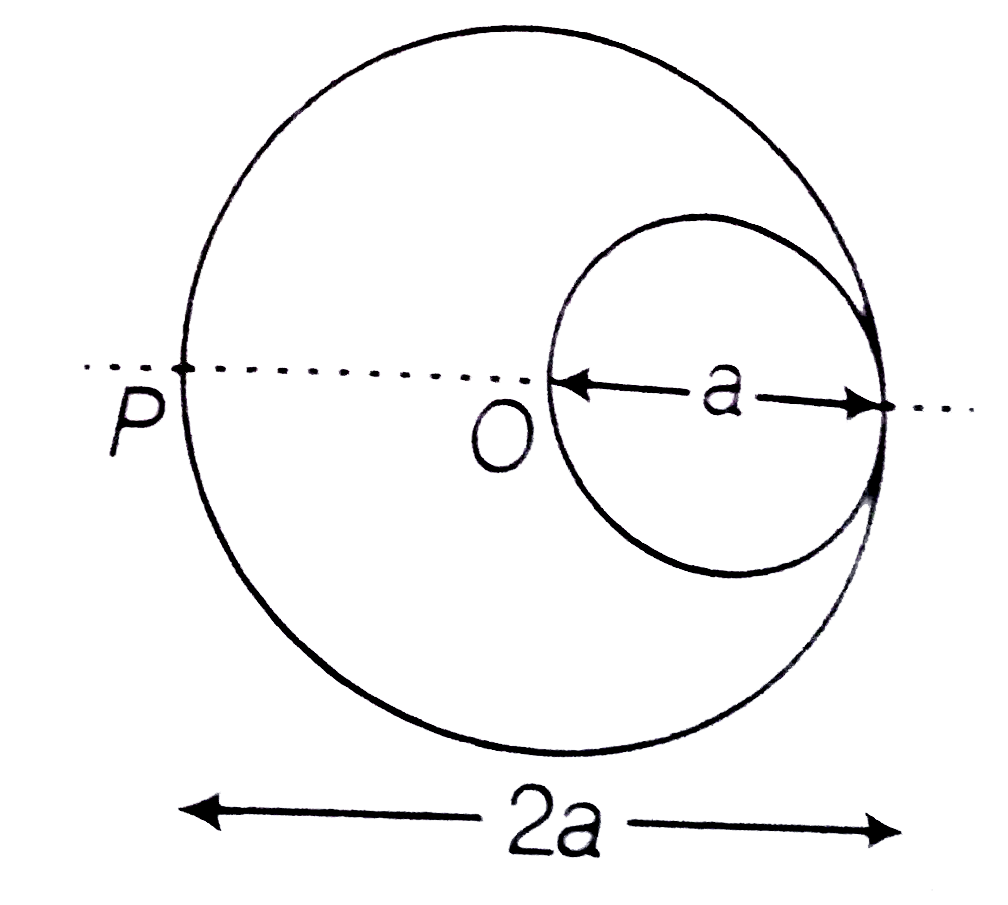
View Solution
An infinity long cylinder of radius R has an infinitely long cylindrical cavity of radius R2 are shown in the figure. The remaining portion has uniform volume charge density ρ. The magnitude of electrical field at the centre of the cavity is-
View Solution
Knowledge Check
Inside a long straight uniform wire of round cross-section, there is a long round cylindrical cavity whose axis is parallel to the axis of the wire and displaced from the latter by a distance l. A direct current of density j flows along the wire. Find the magnetic induction inside the cavity. Consider, in particular, the case l=0.
 A0B12μ0→J×→dCμ0→J×→dD32μ0→J×→d
A0B12μ0→J×→dCμ0→J×→dD32μ0→J×→d
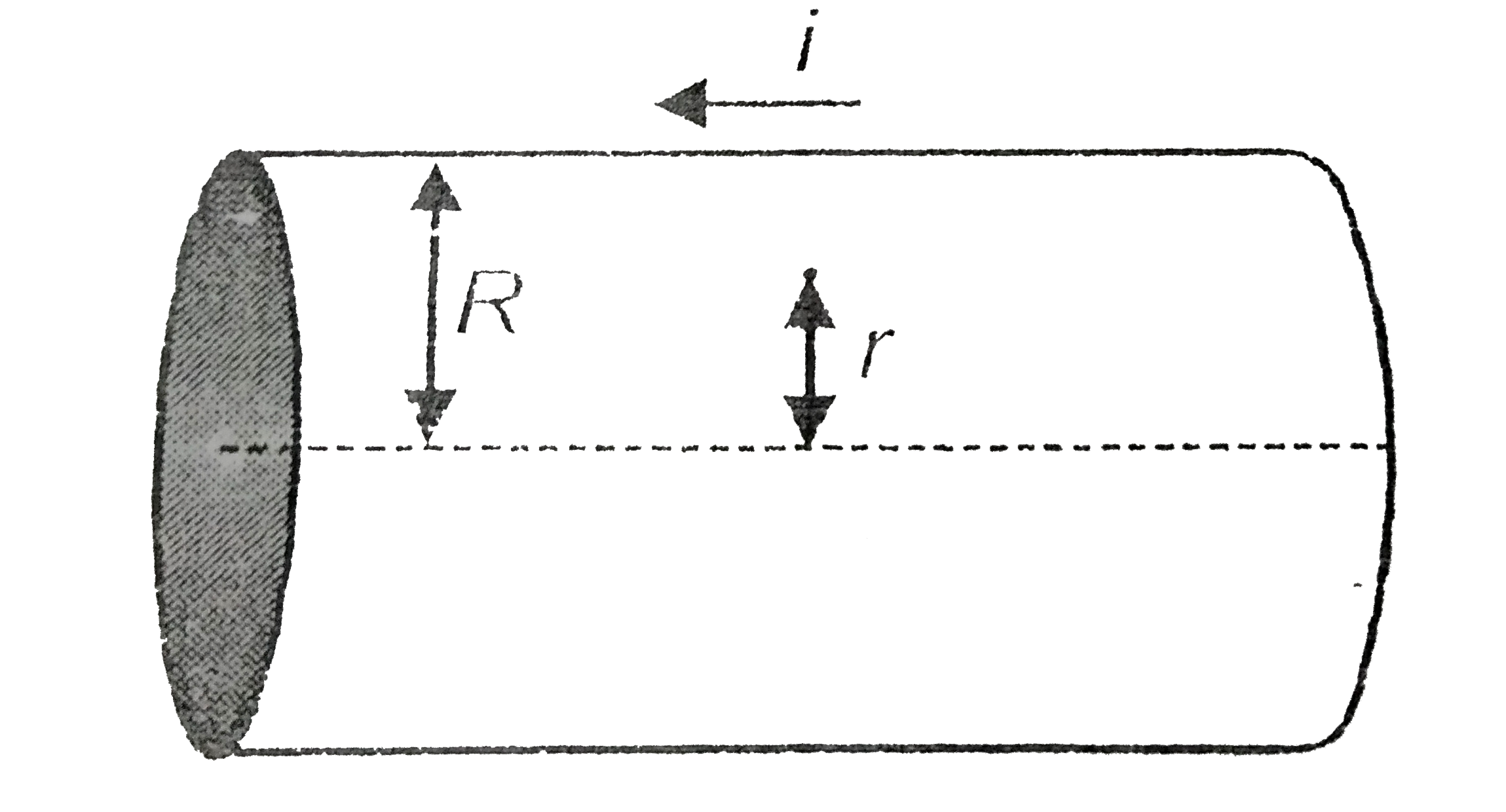
A thin but long, hollow, cylindrical tube of radius r carries a current i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
View SolutionAn infinitely long hollow conducting cylinder with inner radius R2 and outer radius R carries a uniform current density along its length . The magnitude of the magnetic field , ∣∣→B∣∣ as a function of the radial distance r from the axis is best represented by
View SolutionTwo co-axial hollow cylinders of radius a and 2a having current I and 3I2 in opposite directions respectively as shown in the figure. The ratio of the magnitude of magnetic field at the point P and point Q will be (OP=3a2andOQ=5a2)

View SolutionA long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as J=kr2, where, k is a constant. Find an expression for the magnetic field B at a distance r(<R) from the axis
View SolutionA thin sheet of width 2a is placed in the x-y plane between the lines x=−a and x=a. The sheet is very long in the -y and +y directions. It carries a current l towards the +y direction. This current is uniformly distributed over the width of the sheet. The magnitude of magnetic fiedl at the point P(2a,0) due to the sheet is (1n)(μ0Iπa)loge3. Here the value of n is ______________.
View SolutionFour very long wires are arranged as shown in the figure, so that their cross - section forms a square, with connections at the ends so that current I flow through all four wires. Length of each side of the formed such square is b. The magnetic field at the central point P (centre of the square) is
View SolutionAn infinitely long solid cylinder of radius R has a uniform volume charge density ρ. It has a spherical cavity of radius R/2 with its centre on the axis of cylinder, as shown in the figure. The magnitude of the electric field at the point P, which is at a distance 2R form the axis of the cylinder, is given by the expression 23rR16ke0 . The value of k is .
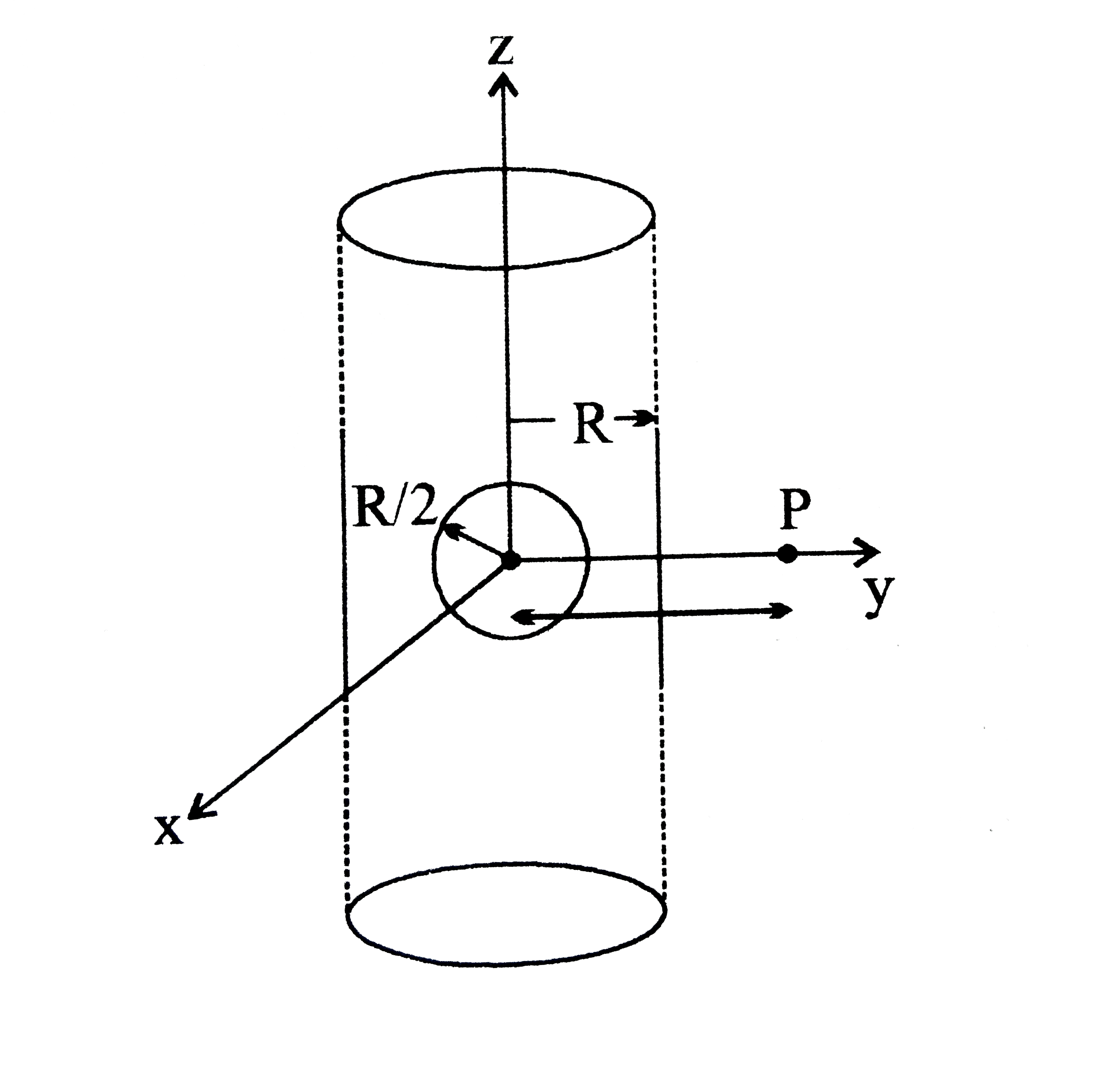 .
.
View Solution
