A cylinderical cavity of diameter a exists inside a cylinder of diameter 2a as shown in the figure. Both the cylinder and the cavity are infinitely long. A uniform current density J flows along the length. If the magnitude of the magnetic field at the point P is given by N12μ0aJ, then the value of N is
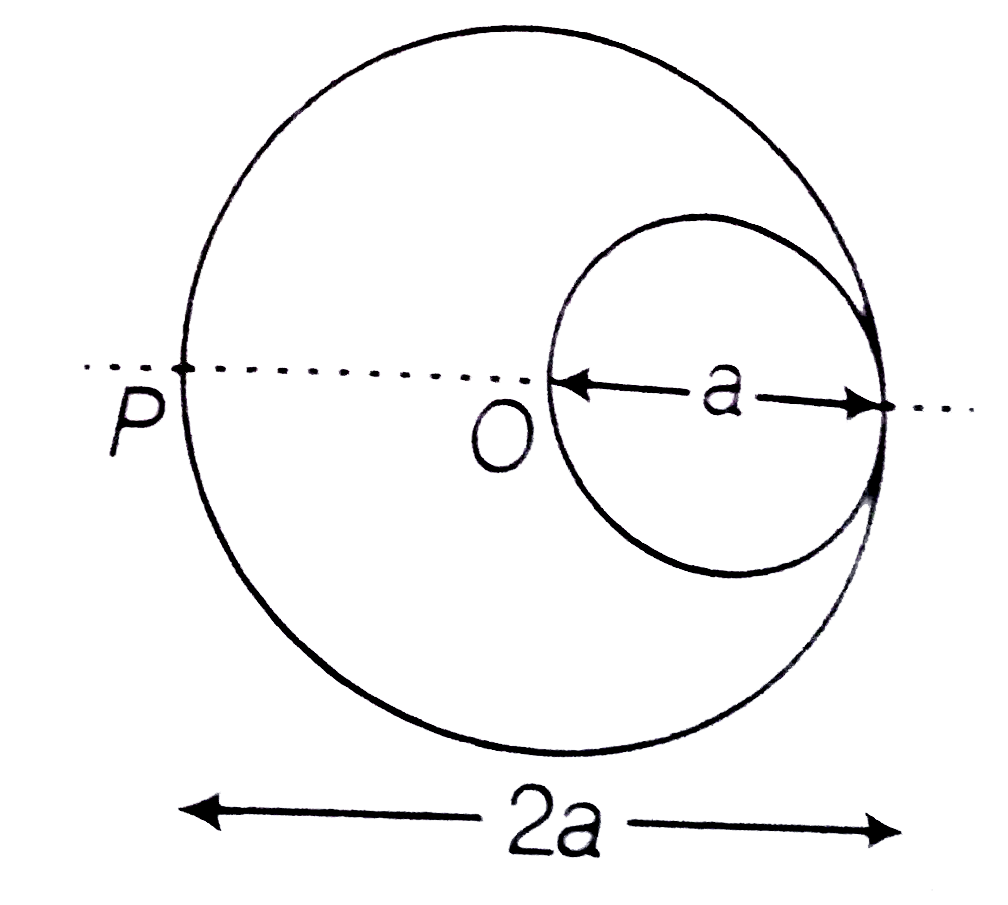
The correct Answer is:5
BR=BT−BC R= remaining portion T= total portion and C= cavity
BR=μ0IT2Aπ−μ0IC2(3a/2)π…….i , IT=J(πa2)IC=J(πa24)
Substituting the value in eq (i) we have BR=μ0aπ[IT2−TC3]=μ0aπ[πa2J2−πa2J12]=5μ0aJ12∴N=5
Related Playlists
- BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Main (Archive)75videos
MAGNETIC EFFECTS OF CURRENT
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)55videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 1EXERCISE - PART I : PHYSICS (SECTION-2)10videos
MOCK TEST 1
Similar Questions
A cylindrical cavity of diameter a exists inside a cylinder of diameter 2a as shown in the figure. Both the cylinder and the cavity are infinitity long. A uniform current density j flows along the length . If the magnitude of the magnetic field at the point P is given by N12μ0Ja, then the value of N is
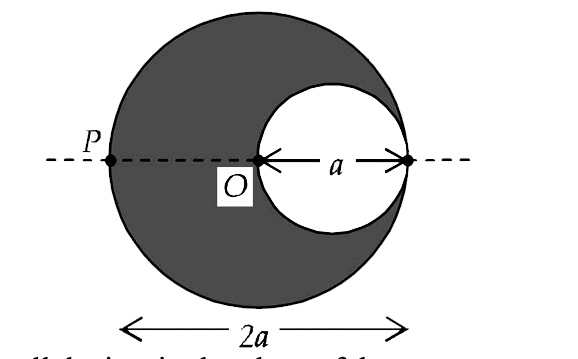 View Solution
View Solution
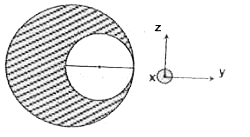
An infinity long cylinder of radius R has an infinitely long cylindrical cavity of radius R2 are shown in the figure. The remaining portion has uniform volume charge density ρ. The magnitude of electrical field at the centre of the cavity is-View SolutionAn infinitely long hollow conducting cylinder with inner radius R2 and outer radius R carries a uniform current density along its length . The magnitude of the magnetic field , ∣∣→B∣∣ as a function of the radial distance r from the axis is best represented by
View SolutionInside a long straight uniform wire of round cross-section, there is a long round cylindrical cavity whose axis is parallel to the axis of the wire and displaced from the latter by a distance l. A direct current of density j flows along the wire. Find the magnetic induction inside the cavity. Consider, in particular, the case l=0.
 View Solution
View SolutionTwo co-axial hollow cylinders of radius a and 2a having current I and 3I2 in opposite directions respectively as shown in the figure. The ratio of the magnitude of magnetic field at the point P and point Q will be (OP=3a2andOQ=5a2)
 View Solution
View SolutionA long cylindrical conductor of radius R having a cylindrical cavity of radius R/2 through out its length is lying with its axis parallel to x-axis. The distance between the axes of the cylinder and the cavity length in the positive x direction. The across sectional view of the cylinder is shown in the figure
The magnetic induction at point on the cavity isView SolutionAn infinitely long solid cylinder of radius R has a uniform volume charge density ρ. It has a spherical cavity of radius R/2 with its centre on the axis of cylinder, as shown in the figure. The magnitude of the electric field at the point P, which is at a distance 2R form the axis of the cylinder, is given by the expression 23rR16ke0 . The value of k is .
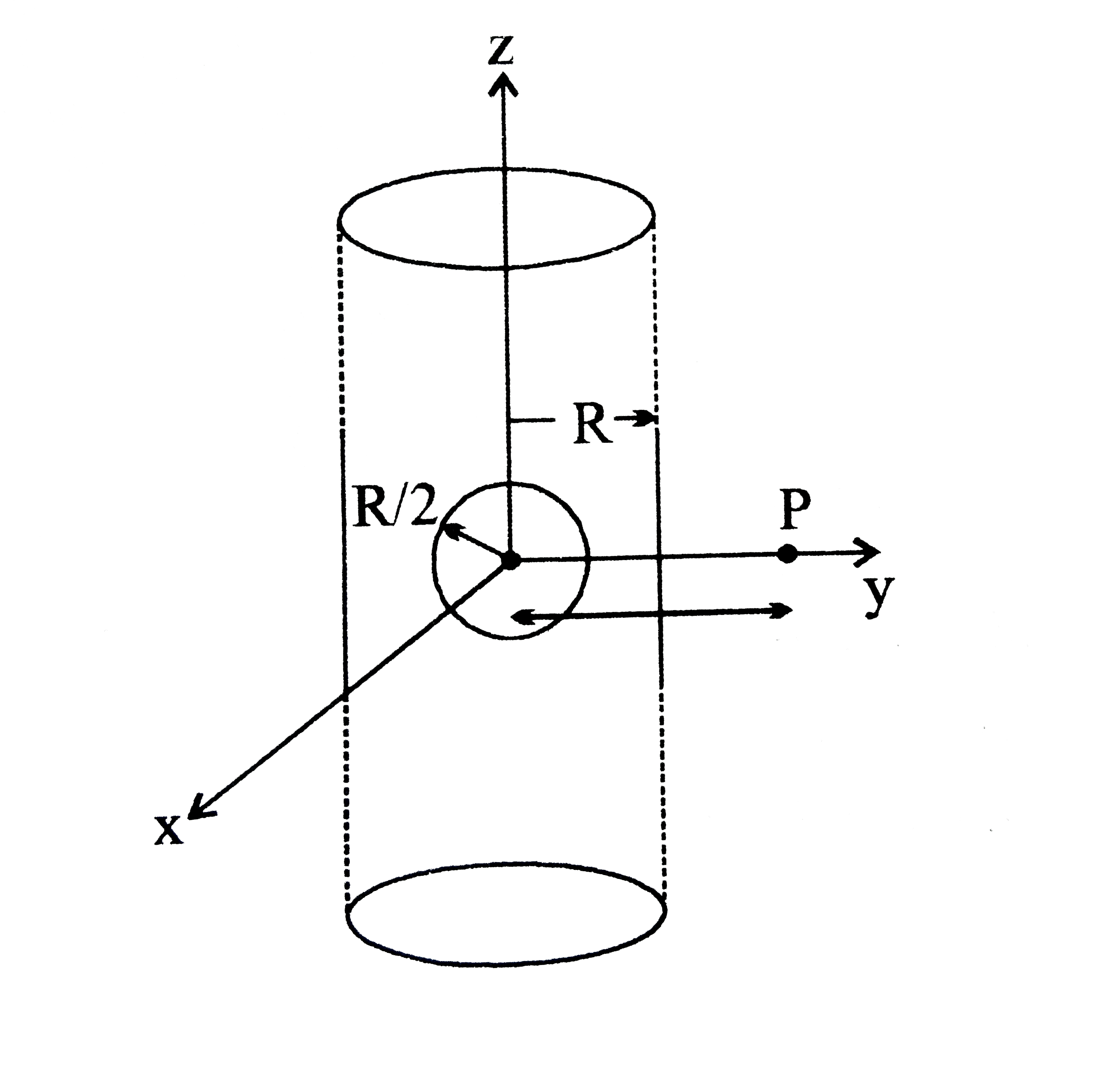 .View Solution
.View SolutionAn electric current I flows through an infinitely long conductor as shown in Figure 2(a) below. Write an expression and direction for the magnetic field at point P.
 View Solution
View SolutionA very long, solid insulating cylinder with radius R has a cylindrical hole with radius a bored along its entire length. The axis of the hole is at a distance b from the axis of the cylinder, where a<b<R (as shown in figure). The solid material of the cylinder has a uniform volume charge density ρ. Find the magnitude and direction of the electric field inside the hole, and show that this is uniform over the entire hole.
 . View Solution
. View SolutionA non - popular loop of conducting wire carrying a current I is placed as shown in the figure . Each of the straighrt sections of the loop is of the length 2a. The magnetic field due to this loop at the point P(a,0,a) points in the direction
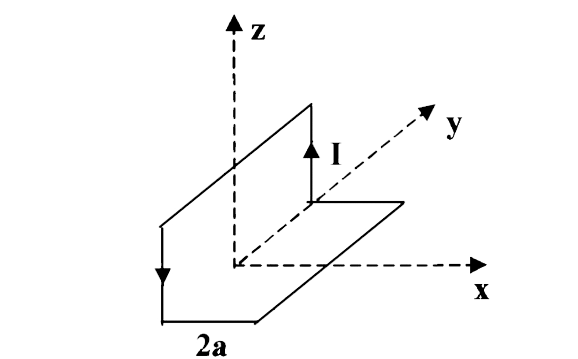 View Solution
View Solution


