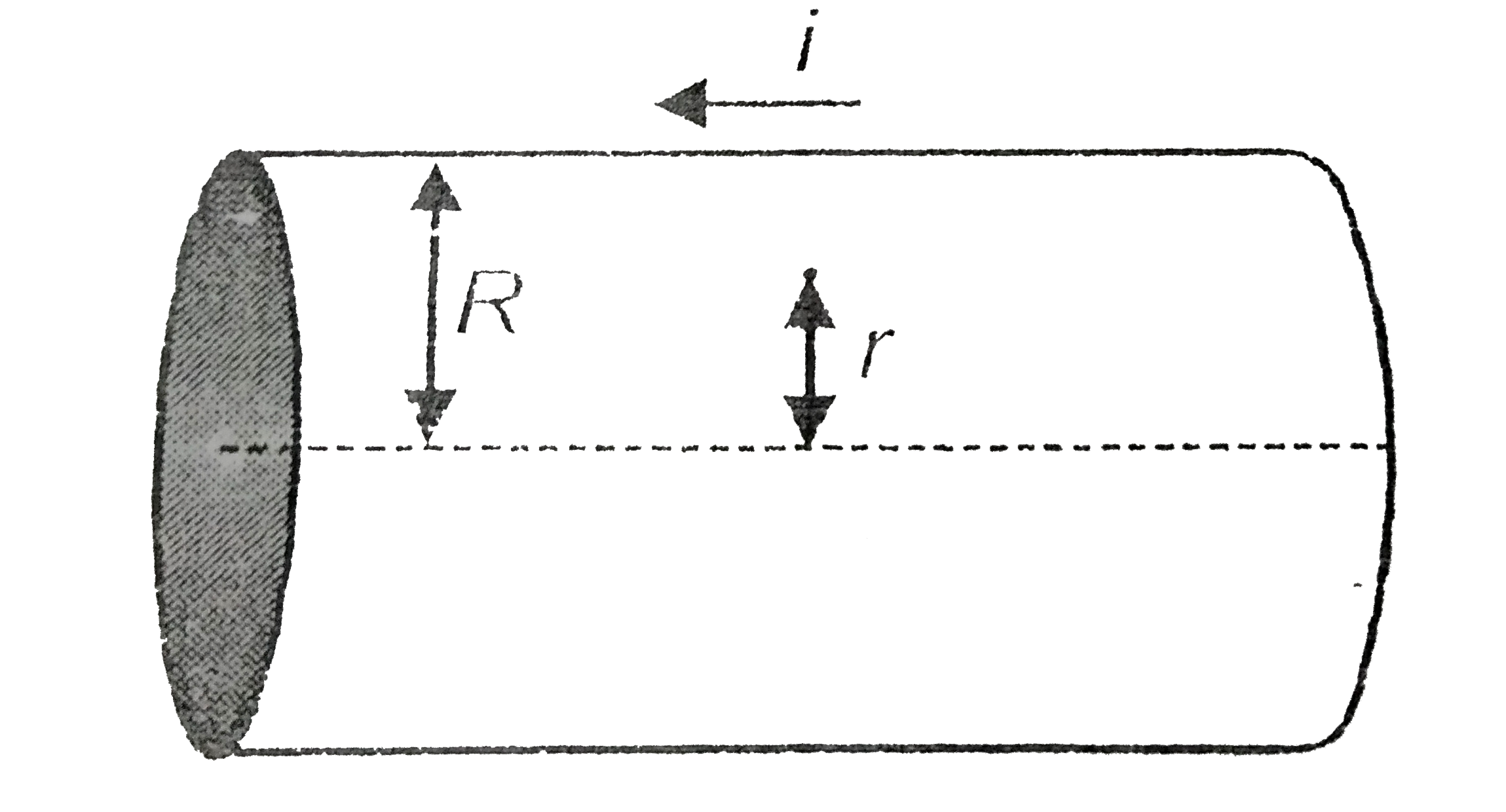
A steady current I flows along an infinitely long hollow cylindrical conductor of radius R. This cylinder is placed coaxially inside an infinite solenoid of radius 2R. The solenoid has a n turns per unit length and carries a steady current I. Consider a point p at a distance r from the common axis . The correct statement(s) is (are)
In the region 0<r<R, the magnetic field is non-zero
In the region R<r<2R, the magnetic field is along the common axis.
In the region R<r<2R, the magnetic field is tangential to the circle of radius r, centred on the axis.
In the region r>2R, the magnetic field in non-zero.
The correct Answer is:A, D
To solve the problem, we need to analyze the magnetic fields produced by both the hollow cylindrical conductor and the infinite solenoid at different regions around them. Let's break it down step by step.
Step 1: Understanding the System
We have:
- An infinitely long hollow cylindrical conductor of radius R carrying a steady current I.
- An infinite solenoid of radius 2R with n turns per unit length, also carrying a steady current I.
- We need to determine the magnetic field at a point P located at a distance r from the common axis of the cylinder and the solenoid.
Step 2: Magnetic Field Inside the Hollow Cylinder
For a hollow cylindrical conductor:
- Inside the conductor (i.e., for r<R), the magnetic field B is zero.
- Outside the conductor (i.e., for r>R), the magnetic field is given by:
B=μ0I2πr
where μ0 is the permeability of free space.
Step 3: Magnetic Field Inside the Solenoid
For an infinite solenoid:
- Inside the solenoid (i.e., for r<2R), the magnetic field B is constant and given by:
B=μ0nI
- Outside the solenoid (i.e., for r>2R), the magnetic field is zero.
Step 4: Analyzing Different Regions
Now, we will analyze the magnetic field in different regions based on the distance r:
1. Region 1: 0<r<R
- Inside the hollow cylinder, B=0.
- Inside the solenoid, B=μ0nI.
- Conclusion: The magnetic field is non-zero and equal to μ0nI.
2. Region 2: R<r<2R
- Outside the hollow cylinder, B=μ0I2πr.
- Inside the solenoid, B=μ0nI.
- The magnetic fields from the solenoid and the hollow cylinder will have different directions. The net magnetic field will not be along the common axis.
- Conclusion: The magnetic field is not along the common axis.
3. Region 3: 2R<r
- Outside both the hollow cylinder and the solenoid, the magnetic field from the solenoid is zero.
- The magnetic field from the hollow cylinder is μ0I2πr.
- Conclusion: The magnetic field is non-zero.
Final Conclusion
Based on the analysis:
- Option A: Correct (non-zero magnetic field in 0<r<R).
- Option B: Incorrect (the magnetic field is not along the common axis in R<r<2R).
- Option C: Incorrect (the magnetic field is not tangential in 2R<r).
- Option D: Correct (non-zero magnetic field in r>2R).
Correct Statements:
The correct statements are A and D.
---
We have:
- An infinitely long hollow cylindrical conductor of radius R carrying a steady current I.
- An infinite solenoid of radius 2R with n turns per unit length, also carrying a steady current I.
- We need to determine the magnetic field at a point P located at a distance r from the common axis of the cylinder and the solenoid.
For a hollow cylindrical conductor:
- Inside the conductor (i.e., for r<R), the magnetic field B is zero.
- Outside the conductor (i.e., for r>R), the magnetic field is given by:
B=μ0I2πr
where μ0 is the permeability of free space.
For an infinite solenoid:
- Inside the solenoid (i.e., for r<2R), the magnetic field B is constant and given by:
B=μ0nI
- Outside the solenoid (i.e., for r>2R), the magnetic field is zero.
Now, we will analyze the magnetic field in different regions based on the distance r:
- Inside the hollow cylinder, B=0.
- Inside the solenoid, B=μ0nI.
- Conclusion: The magnetic field is non-zero and equal to μ0nI.
- Outside the hollow cylinder, B=μ0I2πr.
- Inside the solenoid, B=μ0nI.
- The magnetic fields from the solenoid and the hollow cylinder will have different directions. The net magnetic field will not be along the common axis.
- Conclusion: The magnetic field is not along the common axis.
- Outside both the hollow cylinder and the solenoid, the magnetic field from the solenoid is zero.
- The magnetic field from the hollow cylinder is μ0I2πr.
- Conclusion: The magnetic field is non-zero.
Based on the analysis:
- Option A: Correct (non-zero magnetic field in 0<r<R).
- Option B: Incorrect (the magnetic field is not along the common axis in R<r<2R).
- Option C: Incorrect (the magnetic field is not tangential in 2R<r).
- Option D: Correct (non-zero magnetic field in r>2R).
The correct statements are A and D.
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Archives (linked Comprehension)
4 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Archives (integer)
1 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Archives (single Correct Anser)
13 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
A conducting ring of radius b is placed coaxially in a long solenoid of radius a (b < a) having n turns per unit length. A current i=i0, cosωt flows through the solenoid. The induced emf in the ring is
View SolutionA long solenoid has a radius a and number of turns per unit length is n. If it carries a current i, then the magnetic field on its axis is directly proportional to
View Solution
Knowledge Check
A short soleniod of radius a, number of turns per unit length n1, and length L is kept coaxially inside a very long solenoid of radius b, number of turns per unit length n2. What is the mutual inductance of the system?
Aμ0πb2n1n2LBμ0πa2n1n2L2Cμ0πa2n1n2LDμ0πb2n1n2L2
A current 'I' flows along an infinitely long straight conductor. If 'r' is the perpendicular distance of a point from the lower end of the conductor, then the magnetic induction B is given by
View SolutionA constant direct current of uniform density ˆj is flowing in an infinitely long cylindrical conductor.The conductor contains an infinitely long cylindrical cavity whose axis is parallel to that of the conductor and is a a distance →l from it.What will be the magnetic induction →B at a point inside the cavity at a distance →r from the centre of cavity?
View SolutionFind the magnetic intensity H at the centre of a long solenoid having n turns per unit length and carrying a current i (a) when no material is kept in it and (b) when a long copper rod is inserted in the solenoid.
View SolutionA circular coil of wire of radius 'r' has 'n' turns and carries a current 'I'. The magnetic induction (B) at a point on the axis of the coil at a distance √3r from its centre is
View SolutionA long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as J=kr2, where, k is a constant. Find an expression for the magnetic field B at a distance r(<R) from the axis
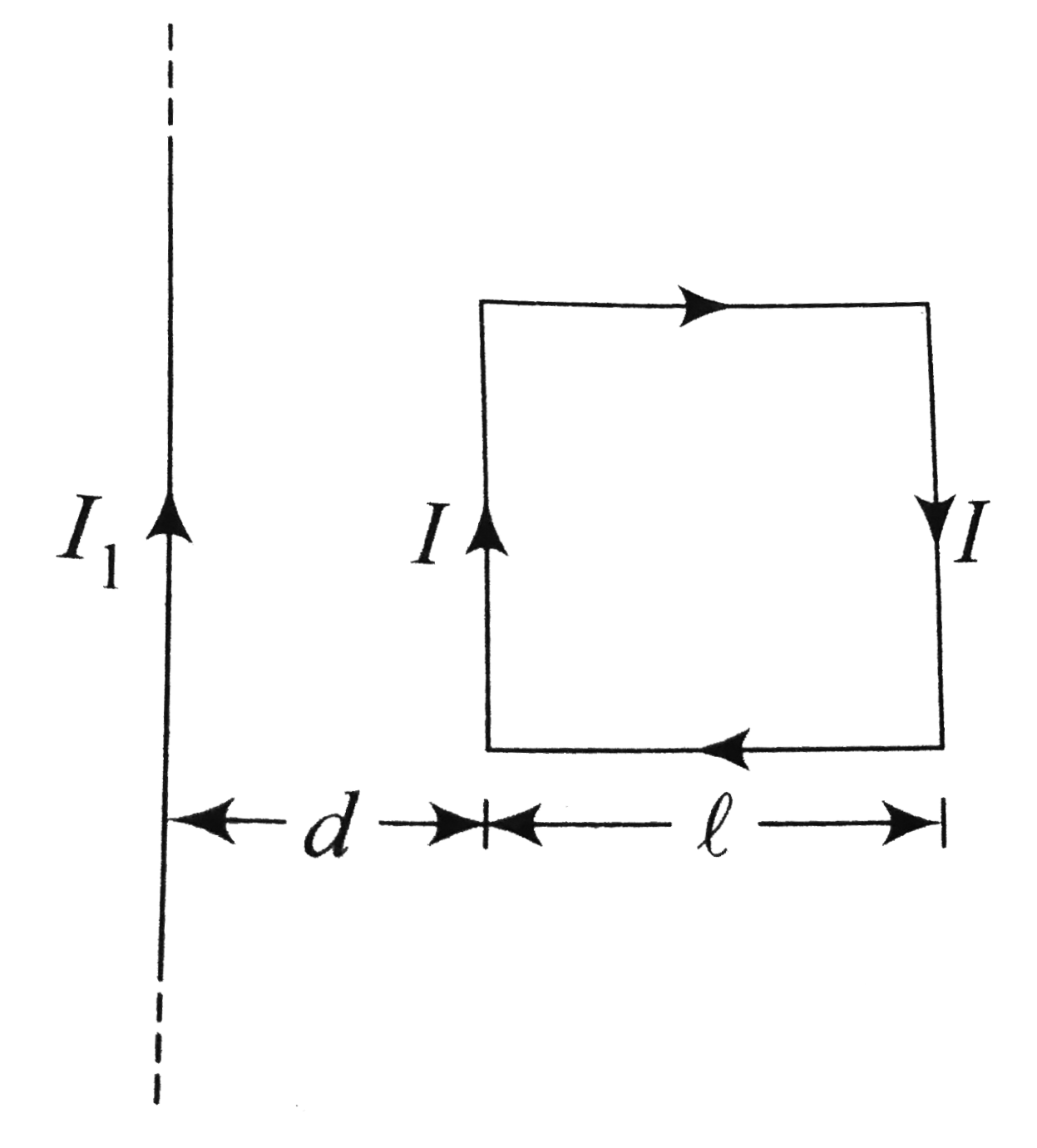
View SolutionA square loop, carrying a steady current I, is placed in a horizontal plane near a long staright conductor carryinf a steady current I, at a distance d from the conductor as shown in Fig. The loop wil experience
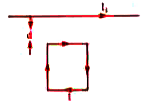
View SolutionA square loop, carrying a steady current I, is placed in a horizontal plane near a long straight conductor carrying a steady current I1 at a distance d from the donductor as shown in figure. The loop will experience
View Solution
