Repeat the above problem, but with the current in both wires shown in fig. directed into the plane of the figure.
At what value of x is the magnitude of →B is maximum?
x=0
x=√2a
x=±a/2
x=±a
The correct Answer is:D
To solve the problem of finding the value of x at which the magnitude of the magnetic field →B is maximum when the currents in both wires are directed into the plane of the figure, we can follow these steps:
Step 1: Understand the Magnetic Field Contribution
The magnetic field →B at a point due to a long straight current-carrying wire is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space, I is the current, and r is the distance from the wire to the point where the magnetic field is being calculated.
Step 2: Set Up the Problem
Assuming we have two parallel wires separated by a distance 2a and carrying currents I into the plane, we need to find the total magnetic field at a point P located at a distance x from the midpoint between the two wires.
Step 3: Calculate the Magnetic Field at Point P
The distance from point P to each wire will be:
- For the wire on the left: r1=x+a
- For the wire on the right: r2=x−a
The magnetic fields due to each wire at point P will be:
B1=μ0I2π(x+a)(from the left wire)
B2=μ0I2π(x−a)(from the right wire)
Since both currents are directed into the plane, the magnetic fields at point P will add up:
B=B1+B2=μ0I2π(x+a)+μ0I2π(x−a)
Step 4: Simplify the Expression for B
Combining the two terms:
B=μ0I2π(1x+a+1x−a)
Finding a common denominator:
B=μ0I2π((x−a)+(x+a)(x+a)(x−a))=μ0I2π(2xx2−a2)
Thus,
B=μ0Ixπ(x2−a2)
Step 5: Find the Maximum Value of B
To find the maximum value of B, we need to differentiate B with respect to x and set the derivative equal to zero:
dBdx=0
Using the quotient rule:
dBdx=π(x2−a2)⋅μ0Iπ−μ0Ix⋅2x(x2−a2)2
Setting the numerator equal to zero:
(x2−a2)−2x2=0⟹−x2+a2=0⟹x2=a2
Thus,
x=±a
Step 6: Determine the Maximum Value
Since we are interested in the maximum value of B, we evaluate at x=a:
- At x=a, the magnetic field will be maximum.
Final Answer
The value of x at which the magnitude of →B is maximum is:
a
The magnetic field →B at a point due to a long straight current-carrying wire is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space, I is the current, and r is the distance from the wire to the point where the magnetic field is being calculated.
Assuming we have two parallel wires separated by a distance 2a and carrying currents I into the plane, we need to find the total magnetic field at a point P located at a distance x from the midpoint between the two wires.
The distance from point P to each wire will be:
- For the wire on the left: r1=x+a
- For the wire on the right: r2=x−a
B1=μ0I2π(x+a)(from the left wire)
B2=μ0I2π(x−a)(from the right wire)
B=B1+B2=μ0I2π(x+a)+μ0I2π(x−a)
Combining the two terms:
B=μ0I2π(1x+a+1x−a)
Finding a common denominator:
B=μ0I2π((x−a)+(x+a)(x+a)(x−a))=μ0I2π(2xx2−a2)
Thus,
B=μ0Ixπ(x2−a2)
To find the maximum value of B, we need to differentiate B with respect to x and set the derivative equal to zero:
dBdx=0
Using the quotient rule:
dBdx=π(x2−a2)⋅μ0Iπ−μ0Ix⋅2x(x2−a2)2
Setting the numerator equal to zero:
(x2−a2)−2x2=0⟹−x2+a2=0⟹x2=a2
Thus,
x=±a
Since we are interested in the maximum value of B, we evaluate at x=a:
- At x=a, the magnetic field will be maximum.
The value of x at which the magnitude of →B is maximum is:
a
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (integer)
7 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Archives (fill In The Blanks)
1 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )
2 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
Repeat the above problem, but with the current in both wires shown in fig. directed into the plane of the figure.
Graph the magnitude of →B at points on the x-axis.
View SolutionRepeat the above problem, but with the current in both wires shown in fig. directed into the plane of the figure.
Derive the expression for the magnitude of →B at any point on the x-axis in terms of the x-coordinate of the point. What is the direciton of →B?
View Solution
Knowledge Check
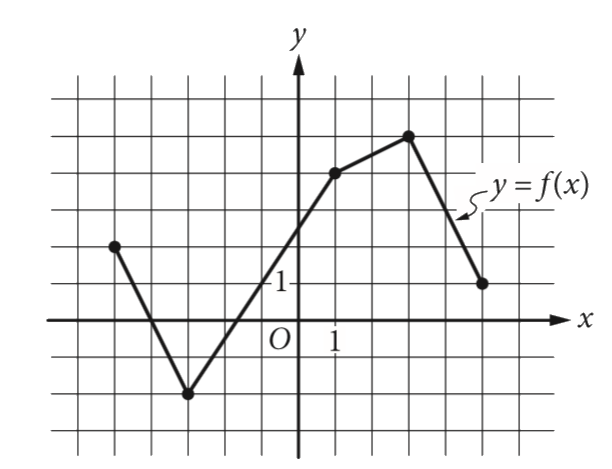
The complete graph of the function f is shown in the xy-plane above. For what value of x is the value of f(x) at its minimum?A−5B−3C−2D3
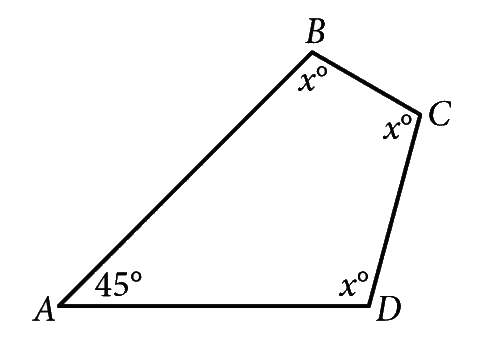
In the figure above, what is the value of x ?
View Solution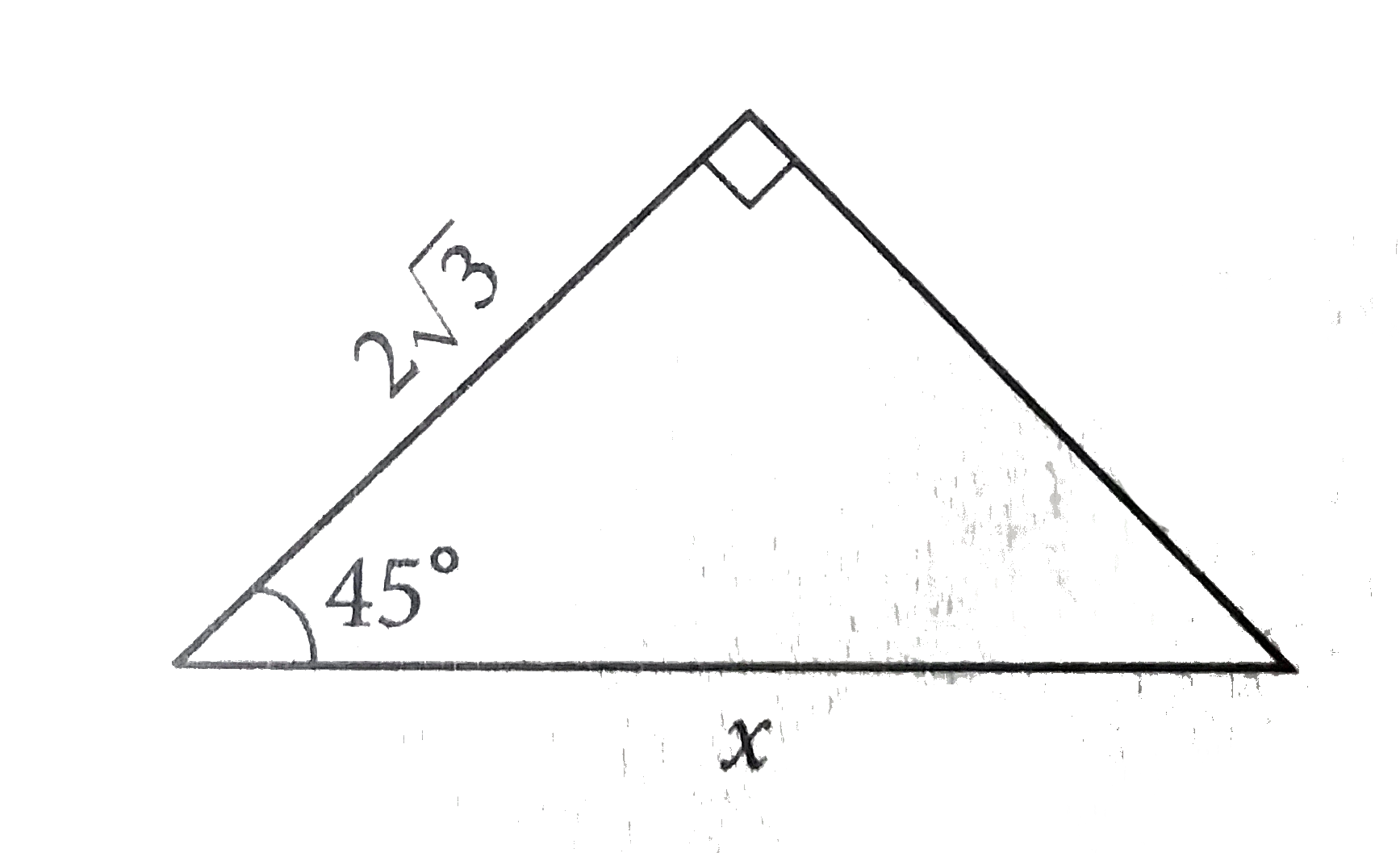
In the figure above, what is the value of x?
View Solution
In the figure above, what is the value of x?
View Solution
In the figure above, what is the value of x?
View SolutionFigure shows an end view of two long, parallel wires perpendicular to the xy plane, each carrying a current I, but in opposite directions.

At what value of x, the magnitude of →B is maxismum?
View Solution
The complete graph of the functions h is shown in the xy plane above. For what value of x is the value of h(x) at its maximum?
View SolutionCurrent I1andI2 flow in the wires shown in Fig. The field is zero at distance x to the right of O. Then
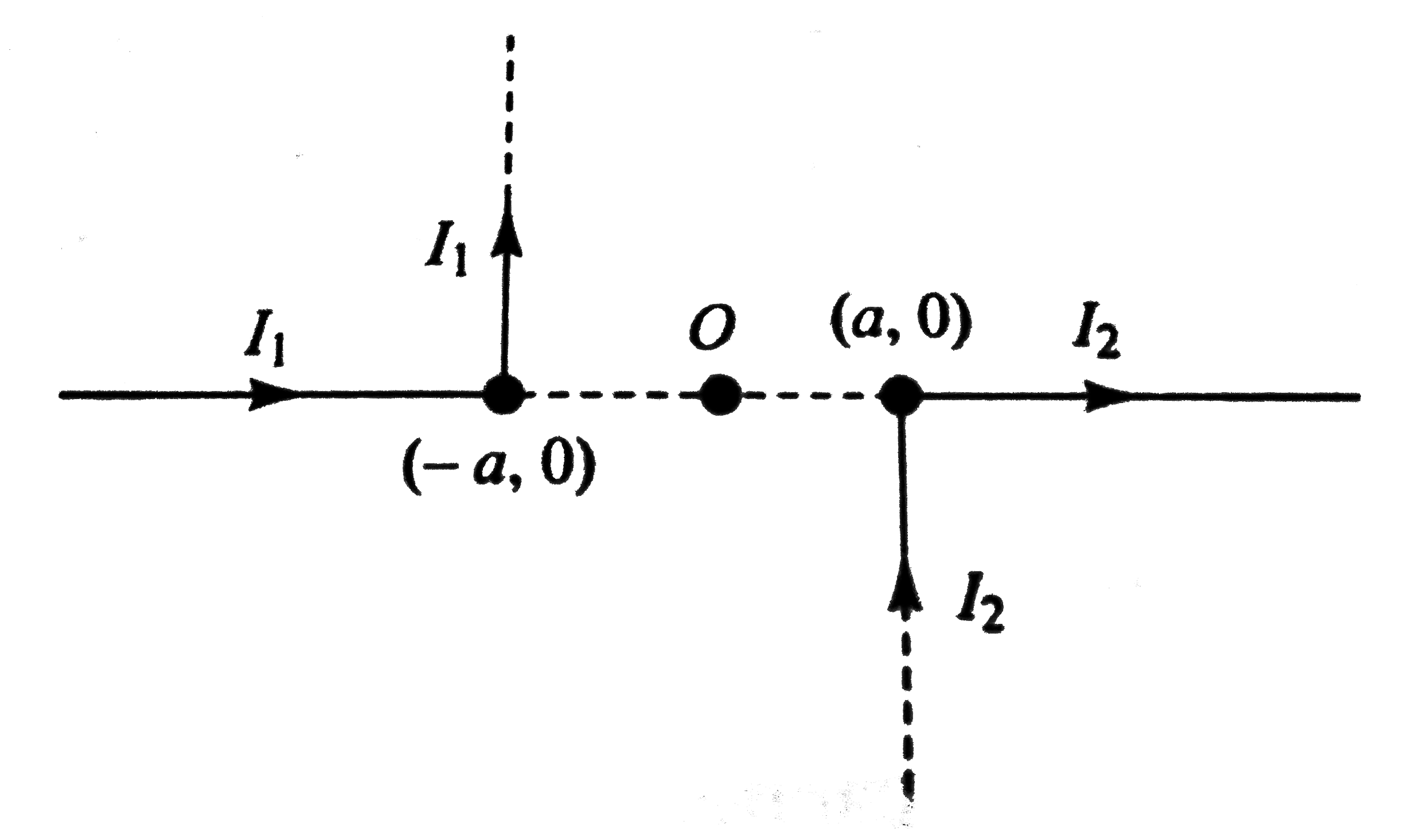
View Solution
