Five very long, straight insulated wires are closely bound together to form a small cable. Currents carried by the wires are: I1=20A,I2=−6A,I3=12A,I4=−7A,I5=18A. (Negative currents are opposite in direction to the positve.) The magnetic field induction at a distance of 10cm from the cable is (current enters at A and leaves at B and C as shown)
5μT
15μT
74μT
128μT
The correct Answer is:C
To solve the problem of finding the magnetic field induction at a distance of 10 cm from a cable formed by five long, straight insulated wires carrying different currents, we will use Ampere's circuital law. Here is the step-by-step solution:
Step 1: Identify the currents
The currents carried by the wires are:
- I1=20A (positive direction)
- I2=−6A (opposite direction)
- I3=12A (positive direction)
- I4=−7A (opposite direction)
- I5=18A (positive direction)
Step 2: Calculate the net current
To find the net current Inet, we sum the individual currents:
Inet=I1+I2+I3+I4+I5
Substituting the values:
Inet=20−6+12−7+18=37A
Step 3: Apply Ampere's Circuital Law
According to Ampere's circuital law:
∮B⋅dl=μ0Inet
For a circular path of radius r, the left side becomes:
B⋅2πr
Thus, we have:
B⋅2πr=μ0Inet
Step 4: Substitute the values
We know:
- r=10cm=0.1m
- μ0=4π×10−7T m/A
Substituting these values into the equation:
B⋅2π(0.1)=4π×10−7×37
Step 5: Simplify the equation
Cancelling 2π from both sides:
B⋅0.2=4×10−7×37
B=4×10−7×370.2
Step 6: Calculate B
Calculating the right-hand side:
B=148×10−70.2=740×10−7T
B=74×10−6T=74μT
Final Answer
The magnetic field induction at a distance of 10 cm from the cable is:
B=74μT
The currents carried by the wires are:
- I1=20A (positive direction)
- I2=−6A (opposite direction)
- I3=12A (positive direction)
- I4=−7A (opposite direction)
- I5=18A (positive direction)
To find the net current Inet, we sum the individual currents:
Inet=I1+I2+I3+I4+I5
Substituting the values:
Inet=20−6+12−7+18=37A
According to Ampere's circuital law:
∮B⋅dl=μ0Inet
For a circular path of radius r, the left side becomes:
B⋅2πr
Thus, we have:
B⋅2πr=μ0Inet
We know:
- r=10cm=0.1m
- μ0=4π×10−7T m/A
B⋅2π(0.1)=4π×10−7×37
Cancelling 2π from both sides:
B⋅0.2=4×10−7×37
B=4×10−7×370.2
Calculating the right-hand side:
B=148×10−70.2=740×10−7T
B=74×10−6T=74μT
The magnetic field induction at a distance of 10 cm from the cable is:
B=74μT
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (multiple Currect )
5 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )
2 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )
10 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
The magnetic field at a distance r from a long wire carryimg current I is 0.4 T. The magnetic field at a distance 2r is
View SolutionA long straight wire carries an electric current of 2A. The magnetic induction at a perpendicular distance of 5m from the wire is (μ04π×107Hm−1)
View SolutionA wire loop carrying current I is placed in the x-y plane as shown. Magnetic induction at P is
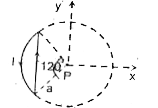
View SolutionTwo long straight wires, each carrying a current I in opposite directions are separated by a distance R. The magnetic induction at a point mid way between the wire is
View SolutionA long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is

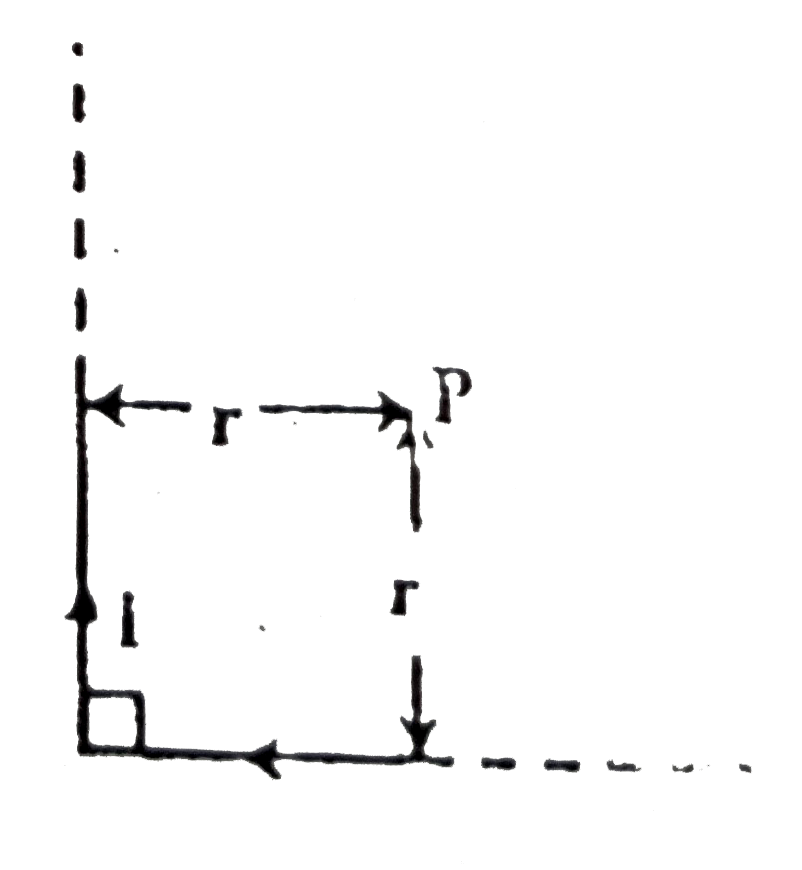
View SolutionThe segment of wire shown in figure carries a current of i=5 A. The magnetic field (in Tesla) at the point P is

View SolutionThe magnetic field strength at a point P distant r due to an infinite straight wire carrying a current i is as shown in the figure
View SolutionTwo very long, straight, and insulated wires are kept at 90∘ angle from each other in xy-plane as shown in the figure. These wires carry currents of equal magnitude I, whose directions are shown in the figure. The net magnetic field at point will be:

View SolutionA long straight wire is carrying a current of 12 A . The magnetic field at a distance of 8 cm is
(μ0=4π×10−7NA2)
View SolutionTwo very long straight , and insulated wires are Kept at 90∘ angle from each other in xy-plane as shown in the figure.
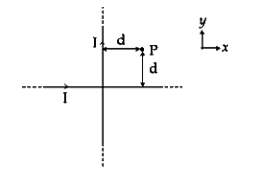 These wires carry current of equal magnitude I, whose direction are shown in the figure The net magnetic field at point P will be:
These wires carry current of equal magnitude I, whose direction are shown in the figure The net magnetic field at point P will be:
View Solution
