A charge q coulomb moves in a circle at n revolution per second and the radius of the circle is r metre. Then magnetic feild at the centre of the circle is
The correct Answer is:C
To find the magnetic field at the center of a circular path where a charge q is moving, we can follow these steps:
1. Identify the Given Information:
- Charge q (in coulombs)
- Frequency of revolution n (in revolutions per second)
- Radius of the circle r (in meters)
2. Relate Current to Charge and Time:
- The current I due to the moving charge can be expressed as:
I=QT
- Where T is the time period for one revolution. Since the frequency n is given, we can find T as:
T=1n
3. Substitute for Current:
- Substitute T into the current equation:
I=Qn
- Therefore, the current I is equal to q⋅n.
4. Use the Formula for Magnetic Field:
- The magnetic field B at the center of a circular path due to a current I is given by:
B=μ0I2r
- Where μ0 is the permeability of free space, approximately 4π×10−7T m/A.
5. Substitute the Current into the Magnetic Field Formula:
- Substitute I=qn into the magnetic field equation:
B=μ0(qn)2r
6. Final Expression for Magnetic Field:
- Now substituting the value of μ0:
B=4π×10−7⋅qn2r
- Simplifying this gives:
B=2πqnr×10−7T
Conclusion:
The magnetic field at the center of the circle is:
B=2πqnr×10−7T
- Charge q (in coulombs)
- Frequency of revolution n (in revolutions per second)
- Radius of the circle r (in meters)
- The current I due to the moving charge can be expressed as:
I=QT
- Where T is the time period for one revolution. Since the frequency n is given, we can find T as:
T=1n
- Substitute T into the current equation:
I=Qn
- Therefore, the current I is equal to q⋅n.
- The magnetic field B at the center of a circular path due to a current I is given by:
B=μ0I2r
- Where μ0 is the permeability of free space, approximately 4π×10−7T m/A.
- Substitute I=qn into the magnetic field equation:
B=μ0(qn)2r
- Now substituting the value of μ0:
B=4π×10−7⋅qn2r
- Simplifying this gives:
B=2πqnr×10−7T
The magnetic field at the center of the circle is:
B=2πqnr×10−7T
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (multiple Currect )
Explore 5 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (assertion-reasioning )
Explore 2 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (subjective )
Explore 10 Videos
- RAY OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:RAY OPTICSExercise:DPP 1.6
Explore 12 Videos
- WAVE OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:WAVE OPTICSExercise:Comprehension Type
Explore 14 Videos
Similar Questions
An electron makes (3×105) revolutions per second in a circle of radius 0.5 angstrom. Find the magnetic field B at the centre of the circle.
View SolutionAn infinitely long conductor is bent into a circle as shown in figure. It carries a current I ampere and the radius of loop is R metre. The magnetic induction at the centre of loop is
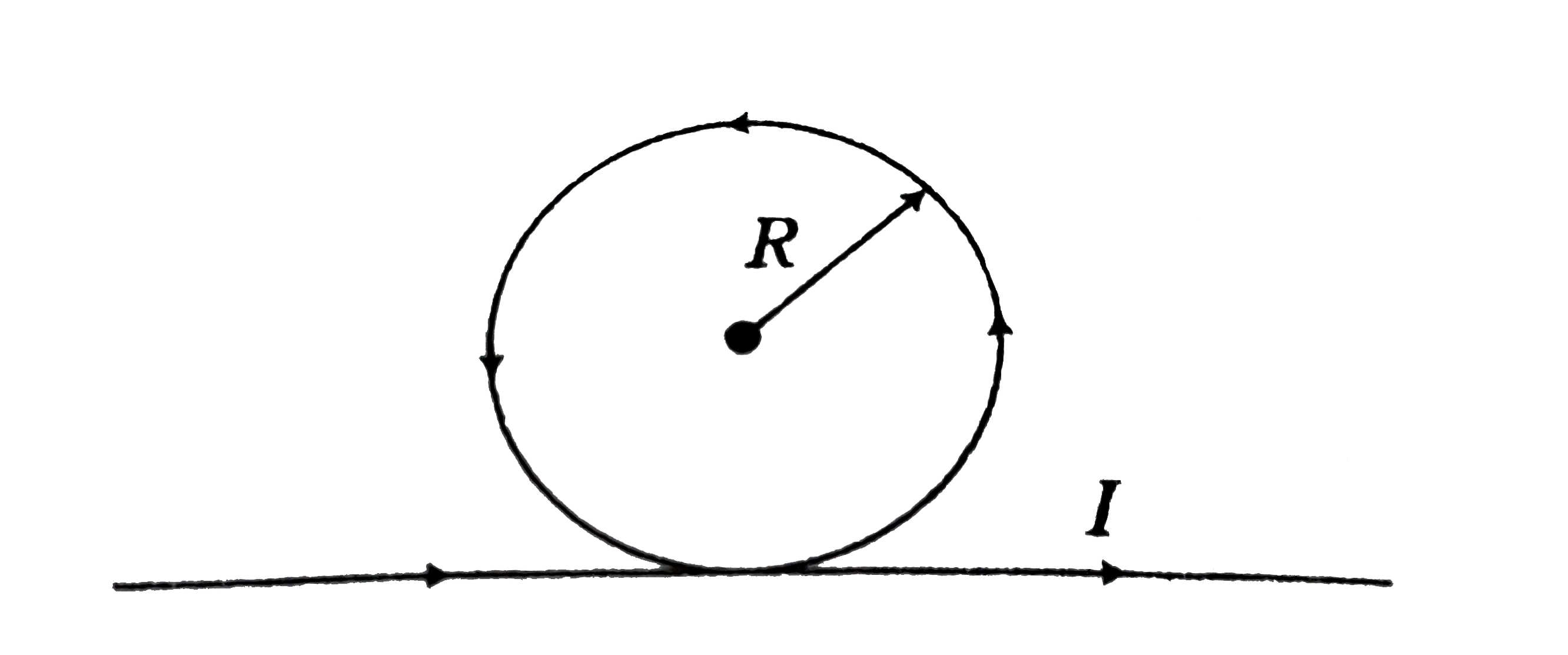
View SolutionA charge of 10−6C is describing a circular path of radius 1cm making 5 revolution per second. The magnetic induction field at the centre of the circle is
View SolutionA particle moving in uniform circle makes 18 revolutions in 1 minutes. If the radius of the circle is 10 cm, the speed of the particle is
View SolutionA particle moves in a circle of radius 25 cm at 2 revolution per second. The acceleration of the particle in meter per second2 is
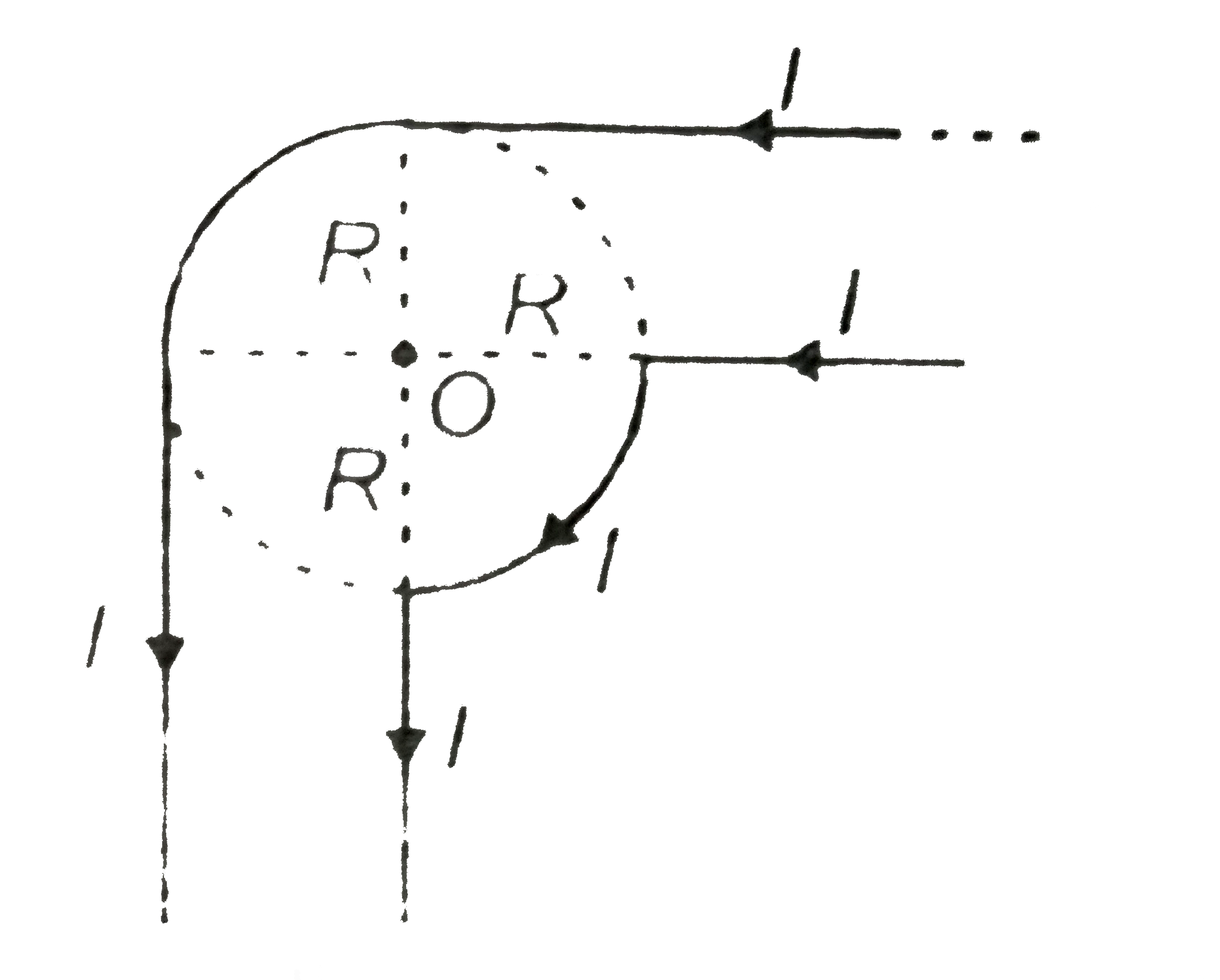
View SolutionThe magnetic field at the centre of dotted circle in the arrangement shown is
View SolutionA charge particle moves in a circle around an infinite line charge with the center of circle at the line and line being perpendicular to the plane of circle. Let r be the radius of circle. The velocity of the particle depends upon which power of r.
View SolutionAn electron moves in a circular orbit with a uniform speed v.It produces a magnetic field B at the centre of the circle. The radius of the circle is proportional to
View SolutionAn electron moves in a circular orbit with a uniform speed v.It produces a magnetic field B at the centre of the circle. The radius of the circle is proportional to
View SolutionA charge q is divided into three equal parts and placed symmetrically on a circle of radius r. The same charge is divided into four equal parts and placed symmetrically on the same circle. The electric field intensities at the centre of the circle in two situations are zero
Q. The ratio of electric potentials at the centre in the two situations is
View Solution
