Find magnetic field at point P shown in Fig. point P is on the bisector of angle between the wires.
To find the magnetic field at point P, which is located on the bisector of the angle between two long parallel wires carrying current, we can follow these steps:
1. Identify the Geometry:
- Let the angle between the two wires be α. Since point P is on the bisector of this angle, the angle between each wire and the bisector is α/2.
2. Determine the Perpendicular Distance:
- If the distance from each wire to point P is x, the perpendicular distance from point P to each wire can be calculated using trigonometry. The perpendicular distance (d) from point P to either wire is given by:
d=xsin(α2)
3. Calculate the Magnetic Field due to One Wire:
- The magnetic field (B) at a distance d from a long straight wire carrying current I is given by the formula:
B=μ0I2πd
- Substituting the value of d from step 2:
B=μ0I2π(xsin(α2))
4. Consider the Contribution from Both Wires:
- Since both wires carry current in the same direction, the magnetic fields at point P due to both wires will be in the same direction. Therefore, the total magnetic field (B_total) at point P is:
Btotal=B1+B2=2B
- Thus:
Btotal=2⋅μ0I2π(xsin(α2))=μ0Iπ(xsin(α2))
5. Final Expression for Magnetic Field:
- The total magnetic field at point P is given by:
Btotal=μ0Iπxsin(α2)
- Let the angle between the two wires be α. Since point P is on the bisector of this angle, the angle between each wire and the bisector is α/2.
- If the distance from each wire to point P is x, the perpendicular distance from point P to each wire can be calculated using trigonometry. The perpendicular distance (d) from point P to either wire is given by:
d=xsin(α2)
- The magnetic field (B) at a distance d from a long straight wire carrying current I is given by the formula:
B=μ0I2πd
- Substituting the value of d from step 2:
B=μ0I2π(xsin(α2))
- Since both wires carry current in the same direction, the magnetic fields at point P due to both wires will be in the same direction. Therefore, the total magnetic field (B_total) at point P is:
Btotal=B1+B2=2B
- Thus:
Btotal=2⋅μ0I2π(xsin(α2))=μ0Iπ(xsin(α2))
- The total magnetic field at point P is given by:
Btotal=μ0Iπxsin(α2)
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.2
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example
20 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
Find the magnetic field at point O shown in the figure

View SolutionFind the magnetic field B at the point P in figure
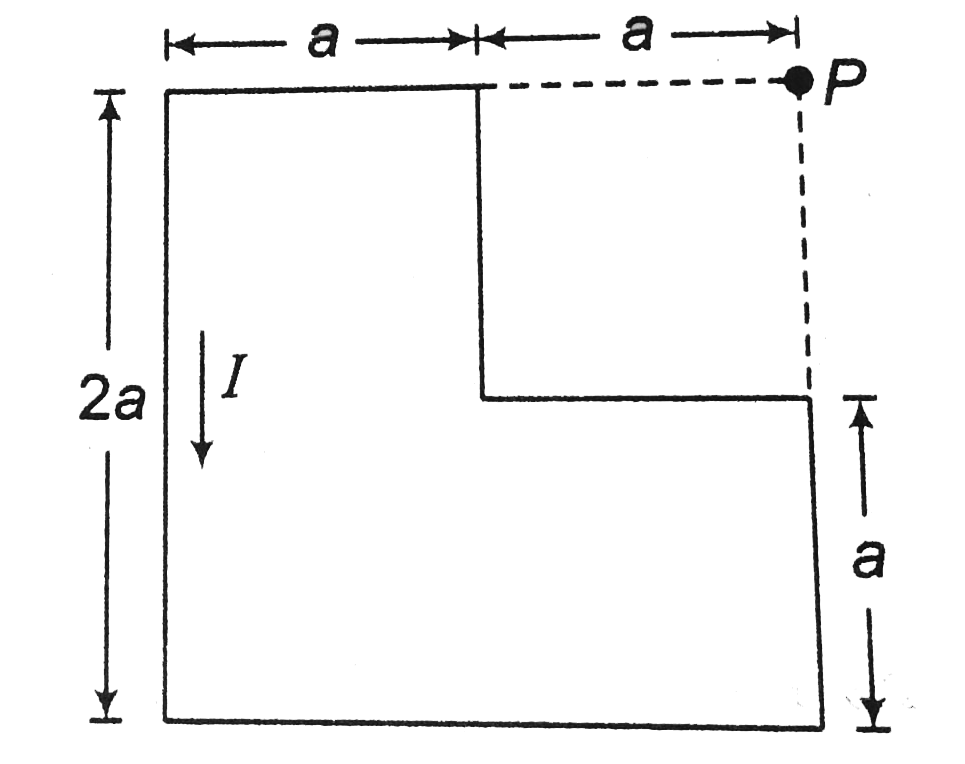
View SolutionIn Fig, find the magnetic field at point P.

View SolutionCurrent I flows through a long conducting wire bent at right angle as shown in Fig. Find the magnetic field at point P on the right angle bisector of the angle XOY at distance r form O.

View SolutionCurrent I flows through a long conducting wire bent at right angle as shown in Fig. Find the magnetic field at point P on the right angle bisector of the angle XOY at distance r form O.

View SolutionFind the magnetic field at the origin in the fig. Shown in fig.

View SolutionCalculate the magnitude of the magnetic field at point P as shown in Fig, in terms of R,I1andI2.

View SolutionFind the magnetic field at the point P in figure. The curved portion is a semicircle and the straight wires are long.

View SolutionA long wire carrying a current i is bent to form a plane angle alpha.Find the magnetic field B at a point on the bisector of this angle situated at a distance x from the vertex.
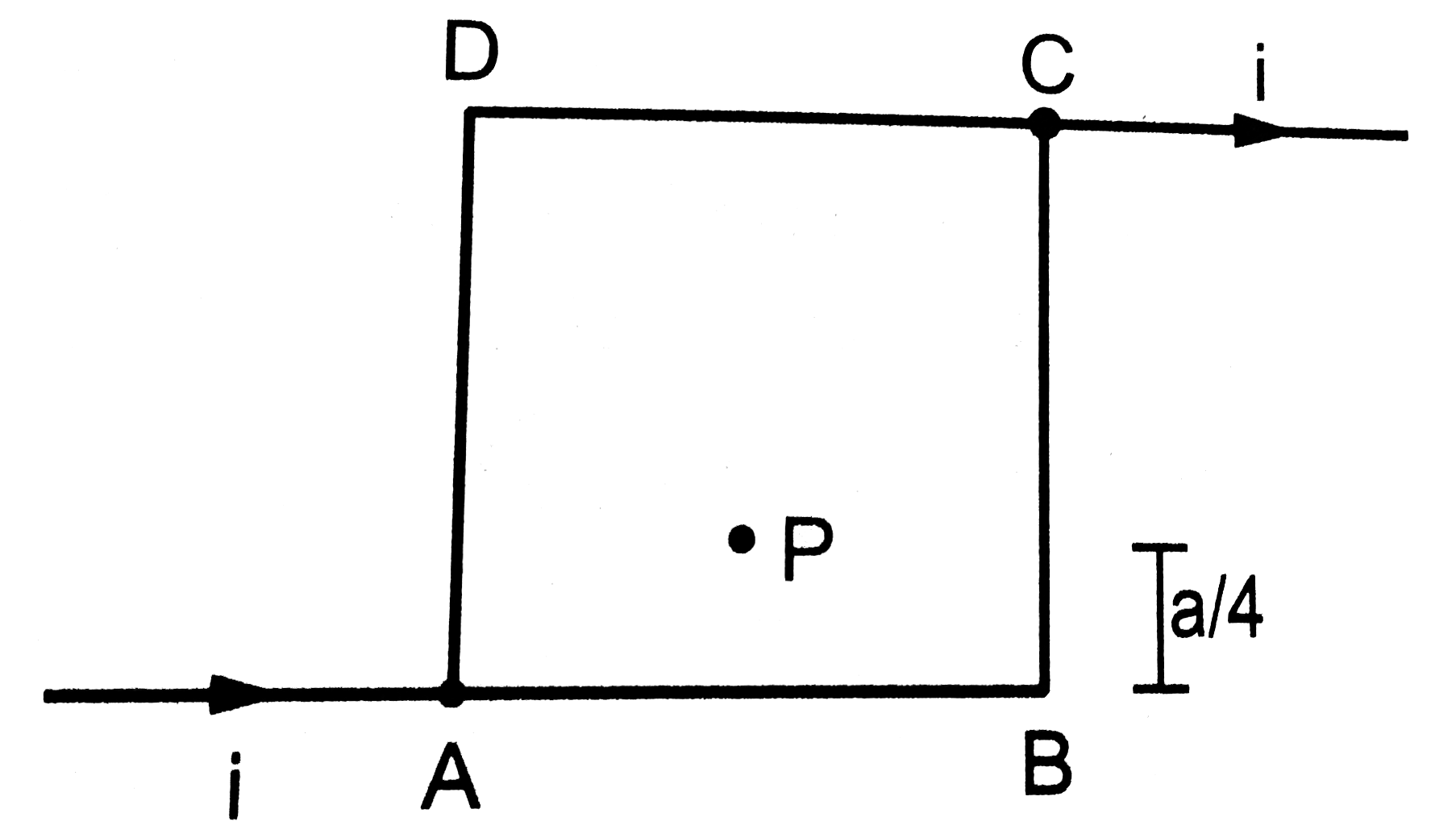
View SolutionFigure shows a square loop of edge a made of a uniform wire. A current i enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.
View Solution
