A long wire carrying a current i is bent to form a plane angle alpha.Find the magnetic field B at a point on the bisector of this angle situated at a distance x from the vertex.
To solve the problem of finding the magnetic field B at a point on the bisector of a plane angle α formed by a long wire carrying a current I, we can follow these steps:
1. Understanding the Geometry:
- We have a long wire bent to form a plane angle α.
- Let the vertex of the angle be point O and the two arms of the wire extend infinitely.
- The bisector of the angle α meets at point P, which is at a distance x from the vertex O.
2. Identifying the Perpendicular Distance:
- The point P is equidistant from both arms of the wire. Let the perpendicular distance from point P to each arm of the wire be d.
- Since P is on the bisector, the angle between the bisector and each arm is α2.
- Using trigonometry, we can find d using the sine function:
d=xsin(α2)
3. Calculating the Angles for Magnetic Field:
- For each arm of the wire, we need to find the angles α1 and α2 that the line connecting point P to the ends of the wire makes with the perpendicular.
- The angle α1=90∘−α2 (for the arm on one side).
- The angle α2=90∘ (for the arm extending to infinity).
4. Using the Formula for Magnetic Field:
- The magnetic field B due to a finite length of wire at a distance d is given by:
B=μ0I4πd(sinα1+sinα2)
- Substituting the values:
B1=μ0I4πd(sin(90∘−α2)+sin(90∘))
- Simplifying, we have:
B1=μ0I4πd(cos(α2)+1)
5. Substituting the Distance d:
- Substitute d=xsin(α2):
B1=μ0I4πxsin(α2)(cos(α2)+1)
6. Calculating the Magnetic Field for Both Wires:
- The magnetic field due to the second wire B2 will have the same magnitude and direction as B1.
- Thus:
B2=B1
7. Finding the Net Magnetic Field:
- The total magnetic field at point P is:
Bnet=B1+B2=2B1
- Therefore:
Bnet=2⋅μ0I4πxsin(α2)(cos(α2)+1)
8. Final Expression:
- After simplification, we arrive at:
Bnet=μ0I2πx⋅cot(α4)
Final Answer:
Bnet=μ0I2πx⋅cot(α4)
- We have a long wire bent to form a plane angle α.
- Let the vertex of the angle be point O and the two arms of the wire extend infinitely.
- The bisector of the angle α meets at point P, which is at a distance x from the vertex O.
- The point P is equidistant from both arms of the wire. Let the perpendicular distance from point P to each arm of the wire be d.
- Since P is on the bisector, the angle between the bisector and each arm is α2.
- Using trigonometry, we can find d using the sine function:
d=xsin(α2)
- For each arm of the wire, we need to find the angles α1 and α2 that the line connecting point P to the ends of the wire makes with the perpendicular.
- The angle α1=90∘−α2 (for the arm on one side).
- The angle α2=90∘ (for the arm extending to infinity).
- The magnetic field B due to a finite length of wire at a distance d is given by:
B=μ0I4πd(sinα1+sinα2)
- Substituting the values:
B1=μ0I4πd(sin(90∘−α2)+sin(90∘))
- Simplifying, we have:
B1=μ0I4πd(cos(α2)+1)
- Substitute d=xsin(α2):
B1=μ0I4πxsin(α2)(cos(α2)+1)
- The magnetic field due to the second wire B2 will have the same magnitude and direction as B1.
- Thus:
B2=B1
- The total magnetic field at point P is:
Bnet=B1+B2=2B1
- Therefore:
Bnet=2⋅μ0I4πxsin(α2)(cos(α2)+1)
- After simplification, we arrive at:
Bnet=μ0I2πx⋅cot(α4)
Bnet=μ0I2πx⋅cot(α4)
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer
12 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 2
7 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Short Answer
6 Videos
Similar Questions
A long wire carrying i is bent to form a plane angle θ.Find the magnetic field B at a point on the bisector of this angle situated at a distance x from the vertex is written in the form of Kcotθ4Tesla.Then, find the value of K.
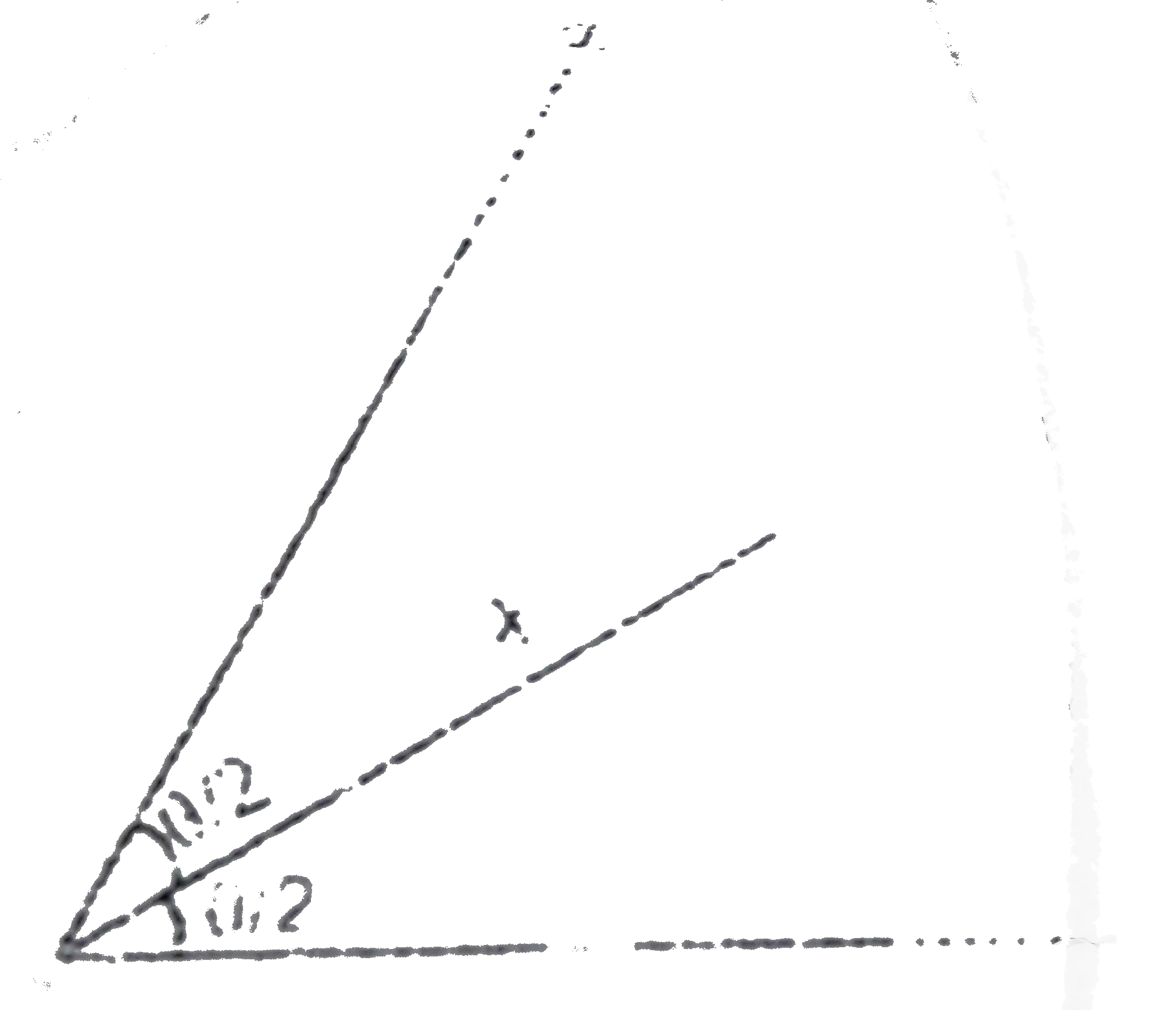
View SolutionA long conducting wire carrying a current I is bent at 120∘( see figure). The magnetic field B at a point P on the right bisector of bending angle at a distance d from the bend is
(μ0 is the permeability of free space)

View Solution(i) A very long wire carrying a current I is bent at right angles .Find magnetic field at a point lying on a perpendicular to the wire , drawn through the point of bending at a distance d from it
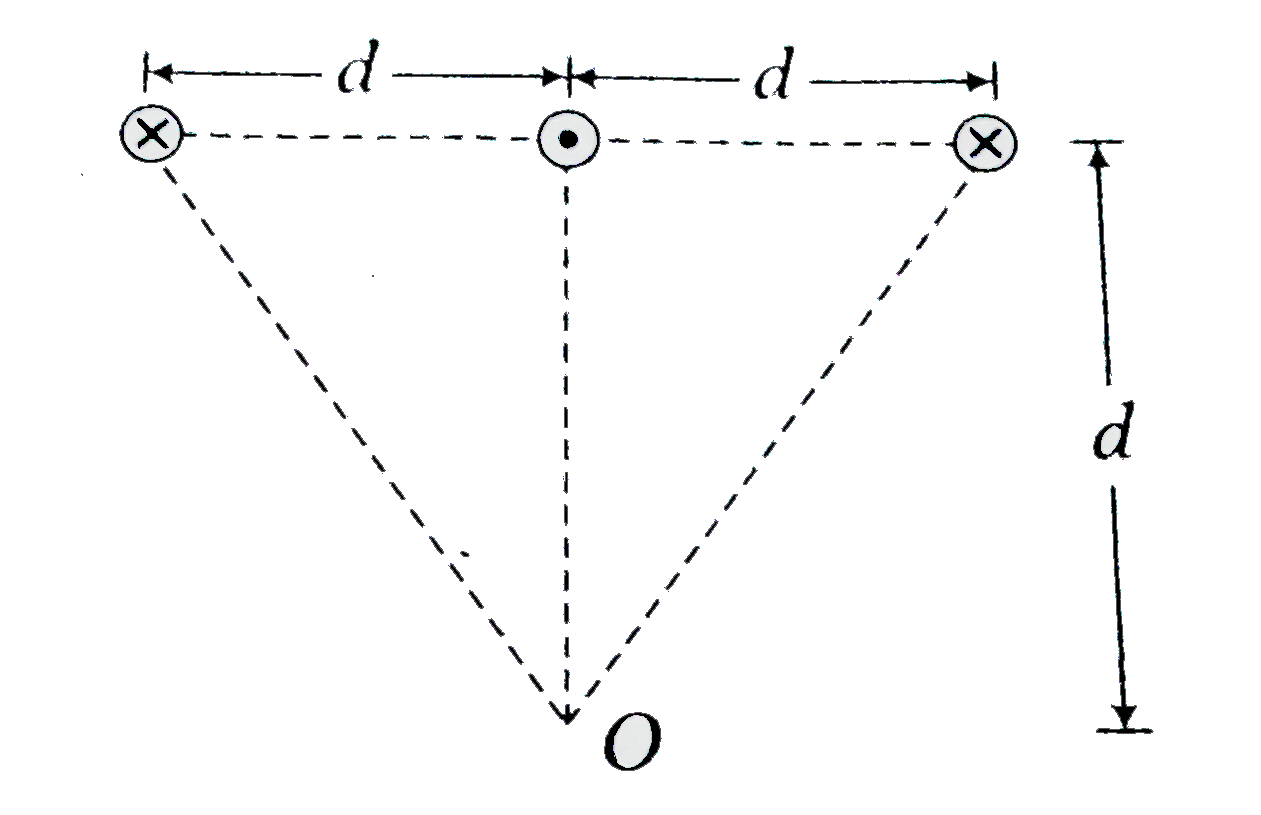
(ii) Three long wires carrying same currect are placed as shown Find magnetic field at O.
View SolutionCurrent I flows through a long conducting wire bent at right angle as shown in Fig. Find the magnetic field at point P on the right angle bisector of the angle XOY at distance r form O.

View SolutionCurrent I flows through a long conducting wire bent at right angle as shown in Fig. Find the magnetic field at point P on the right angle bisector of the angle XOY at distance r form O.

View SolutionA long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is

View SolutionA very long wire carrying a current I=5.0A is bent at right angles. Find the magnetic induction at a point lying on a perpendicular normal to the plane of the wire drawn through the Point of bending at a distance l=35cm from it.
View SolutionFind magnetic field at point P shown in Fig. point P is on the bisector of angle between the wires.
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

View SolutionA long wire carrying a current i=2A is bent at right angles . The magnetic field lying on a perpendicular normal to the plane of the wire draw through the point of bending at distance 1 m form it is ………….Tesla.
View Solution
