Two circular coils of radii 5.0 cm and 10 cm carry equal currents of 2.0 A. The coils have 50 and 100 turns respectively and are placed in such a way that their planes as well as the centres coincide. Find the magnitude of the magnetic field B at the common centre of the coils if the currents in the coils are (a) in the same sense (b) in the opposite sense.
To find the magnitude of the magnetic field B at the common center of two circular coils carrying equal currents, we will analyze the two scenarios: (a) when the currents are in the same direction and (b) when the currents are in opposite directions.
Given Data:
- Radius of Coil 1, R1=5 cm = 5×10−2 m
- Radius of Coil 2, R2=10 cm = 10×10−2 m
- Current in both coils, I1=I2=2 A
- Number of turns in Coil 1, N1=50
- Number of turns in Coil 2, N2=100
(a) When the currents are in the same direction:
1. Magnetic Field due to Coil 1:
The formula for the magnetic field at the center of a circular coil is given by:
B1=μ0N1I12R1
where μ0=4π×10−7T m/A.
Substituting the values:
B1=4π×10−7×50×22×(5×10−2)
Simplifying:
B1=4π×10−7×10010×10−2=4π×10−510=4π×10−6T
2. Magnetic Field due to Coil 2:
Similarly, for Coil 2:
B2=μ0N2I22R2
Substituting the values:
B2=4π×10−7×100×22×(10×10−2)
Simplifying:
B2=4π×10−7×20020×10−2=4π×10−520=2π×10−6T
3. Net Magnetic Field:
Since both magnetic fields are in the same direction, we add them:
Bnet=B1+B2=4π×10−6+2π×10−6=6π×10−6T
(b) When the currents are in opposite directions:
1. Direction of Magnetic Fields:
The magnetic fields B1 and B2 will be in opposite directions.
2. Net Magnetic Field:
Therefore, the net magnetic field at the center will be:
Bnet=B1−B2=4π×10−6−2π×10−6=2π×10−6T
Final Answers:
- (a) When currents are in the same direction: Bnet=6π×10−6T
- (b) When currents are in opposite directions: Bnet=2π×10−6T
- Radius of Coil 1, R1=5 cm = 5×10−2 m
- Radius of Coil 2, R2=10 cm = 10×10−2 m
- Current in both coils, I1=I2=2 A
- Number of turns in Coil 1, N1=50
- Number of turns in Coil 2, N2=100
The formula for the magnetic field at the center of a circular coil is given by:
B1=μ0N1I12R1
where μ0=4π×10−7T m/A.
B1=4π×10−7×50×22×(5×10−2)
Simplifying:
B1=4π×10−7×10010×10−2=4π×10−510=4π×10−6T
Similarly, for Coil 2:
B2=μ0N2I22R2
Substituting the values:
B2=4π×10−7×100×22×(10×10−2)
Simplifying:
B2=4π×10−7×20020×10−2=4π×10−520=2π×10−6T
Since both magnetic fields are in the same direction, we add them:
Bnet=B1+B2=4π×10−6+2π×10−6=6π×10−6T
The magnetic fields B1 and B2 will be in opposite directions.
Therefore, the net magnetic field at the center will be:
Bnet=B1−B2=4π×10−6−2π×10−6=2π×10−6T
- (a) When currents are in the same direction: Bnet=6π×10−6T
- (b) When currents are in opposite directions: Bnet=2π×10−6T
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBook:HC VERMA ENGLISHChapter:MAGNETIC FIELD DUE TO CURRENTExercise:questions for short answer
Explore 12 Videos
- MAGNETIC FIELD DUE TO CURRENTBook:HC VERMA ENGLISHChapter:MAGNETIC FIELD DUE TO CURRENTExercise:Objective 2
Explore 7 Videos
- MAGNETIC FIELDBook:HC VERMA ENGLISHChapter:MAGNETIC FIELDExercise:objective2
Explore 9 Videos
- MAGNETIC PROPERTIES OF MATTERBook:HC VERMA ENGLISHChapter:MAGNETIC PROPERTIES OF MATTERExercise:Short Answer
Explore 6 Videos
Similar Questions
Two circular coils of radii 5.0 cm and 10 cm carry equal currents of 2.0 A. The coils have 50 and 100 turns respectively and are placed in such a way that their planes are perpendicular to each other, what would be the magnitude of the magnetic field B at the centre ?
View SolutionTwo circular coils of radii 5cm and 10cm carry currents of 2A. The coils have 50 and 100 turns respectiely and are placed in such a way that their planes as well as their cetre coincide. Magnitude of magnetic field at the common centre of coils is
View Solution
Knowledge Check
A circular coil of radius 10 cm having 100 turns carries a current of 3.2 A. The magnetic field at the center of the coil is
A2.01×10−3TB5.64×10−3TC2.64×10−3TD5.64×10−3TThe magnitude of the magnetic field at the centre of the tightly wound 150 turn coil of radius 12 cm carrying a current of 2 A is
A18GB19.7GC15.7GD17.7G
The magnetic field at the centre of the current carrying coil is
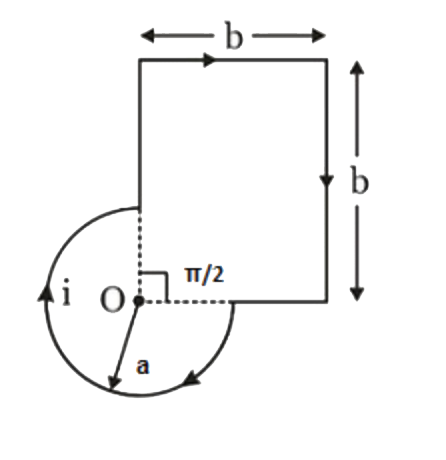
View SolutionThe magnitude of the magnetic field at O ( centre of the circular part ) due to the current - carrying coil as shown is :
View SolutionThe magnetic field at centre of a hexagonal coil of side l carrying a current I is

View SolutionA circular coil of radius 1⋅5cmcarriesacurrentof1⋅5A. If the coil has 25 turns , find the magnetic field at the centre.
View SolutionA tightly wound 100 turn coil of radius 10cm is carrying a current of 1A. What is the magnitude of the magnetic field at the centre of the coil?
View SolutionA circular coil of radius 10cmand100 turns carries a current 1A. What is the magnetic moment of the coil?
View Solution

