A circular loop of radius 4.0 cm is placed in a horizontal plane and carries an electric current of 5.0 A in the clockwise direction as seen from above. Find the magnetic field (a) at a point 3.0 cm above the centre of the loop (b) at a point 3.0 cm below the centre of the loop.
To solve the problem, we need to find the magnetic field at two points: one above the center of the loop and one below it. We will use the formula for the magnetic field along the axis of a circular current-carrying loop.
Given Data:
- Radius of the loop, R=4.0cm=4×10−2m
- Current, I=5.0A
- Distance above the center, X1=3.0cm=3×10−2m
- Distance below the center, X2=3.0cm=3×10−2m
Magnetic Field Formula:
The magnetic field B at a distance x along the axis of a circular loop is given by the formula:
B=μ0IR22(R2+x2)3/2
Where:
- μ0=4π×10−7T m/A (permeability of free space)
Step 1: Calculate the Magnetic Field at Point P1 (3 cm above the center)
1. Substitute the values into the formula for B:
- R=4×10−2m
- I=5.0A
- x=3×10−2m
B1=(4π×10−7)×5×(4×10−2)22((4×10−2)2+(3×10−2)2)3/2
2. Calculate R2 and x2:
- R2=(4×10−2)2=16×10−4m2
- x2=(3×10−2)2=9×10−4m2
3. Calculate R2+x2:
R2+x2=16×10−4+9×10−4=25×10−4m2
4. Calculate (R2+x2)3/2:
(R2+x2)3/2=(25×10−4)3/2=125×10−6m3
5. Substitute back into the equation for B1:
B1=(4π×10−7)×5×16×10−42×125×10−6
6. Simplify:
B1=(20π×16)×10−11250×10−6=320π×10−11250×10−6=320π250×10−5
7. Calculate the final value:
B1=1.28π×10−5T≈4.02×10−5T
Step 2: Calculate the Magnetic Field at Point P2 (3 cm below the center)
Since the magnetic field at point P2 is also at a distance of 3 cm from the center, the calculation will be the same as for point P1. Thus:
B2=B1=4.02×10−5T
Final Answers:
(a) The magnetic field at a point 3.0 cm above the center of the loop is approximately 4.02×10−5T.
(b) The magnetic field at a point 3.0 cm below the center of the loop is also approximately 4.02×10−5T.
- Radius of the loop, R=4.0cm=4×10−2m
- Current, I=5.0A
- Distance above the center, X1=3.0cm=3×10−2m
- Distance below the center, X2=3.0cm=3×10−2m
The magnetic field B at a distance x along the axis of a circular loop is given by the formula:
- μ0=4π×10−7T m/A (permeability of free space)
1. Substitute the values into the formula for B:
- R=4×10−2m
- I=5.0A
- x=3×10−2m
- R2=(4×10−2)2=16×10−4m2
- x2=(3×10−2)2=9×10−4m2
R2+x2=16×10−4+9×10−4=25×10−4m2
(R2+x2)3/2=(25×10−4)3/2=125×10−6m3
B1=(4π×10−7)×5×16×10−42×125×10−6
B1=(20π×16)×10−11250×10−6=320π×10−11250×10−6=320π250×10−5
B1=1.28π×10−5T≈4.02×10−5T
Since the magnetic field at point P2 is also at a distance of 3 cm from the center, the calculation will be the same as for point P1. Thus:
(a) The magnetic field at a point 3.0 cm above the center of the loop is approximately 4.02×10−5T.
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBook:HC VERMA ENGLISHChapter:MAGNETIC FIELD DUE TO CURRENTExercise:questions for short answer
Explore 12 Videos
- MAGNETIC FIELD DUE TO CURRENTBook:HC VERMA ENGLISHChapter:MAGNETIC FIELD DUE TO CURRENTExercise:Objective 2
Explore 7 Videos
- MAGNETIC FIELDBook:HC VERMA ENGLISHChapter:MAGNETIC FIELDExercise:objective2
Explore 9 Videos
- MAGNETIC PROPERTIES OF MATTERBook:HC VERMA ENGLISHChapter:MAGNETIC PROPERTIES OF MATTERExercise:Short Answer
Explore 6 Videos
Similar Questions
A circular loop of radius R=20 cm is placed in a uniform magnetic field B=2T in xy-plane as shown in figure. The loop carries a current i=1.0A in the direction shown in figure. Find the magnitude of torque acting on the loop.
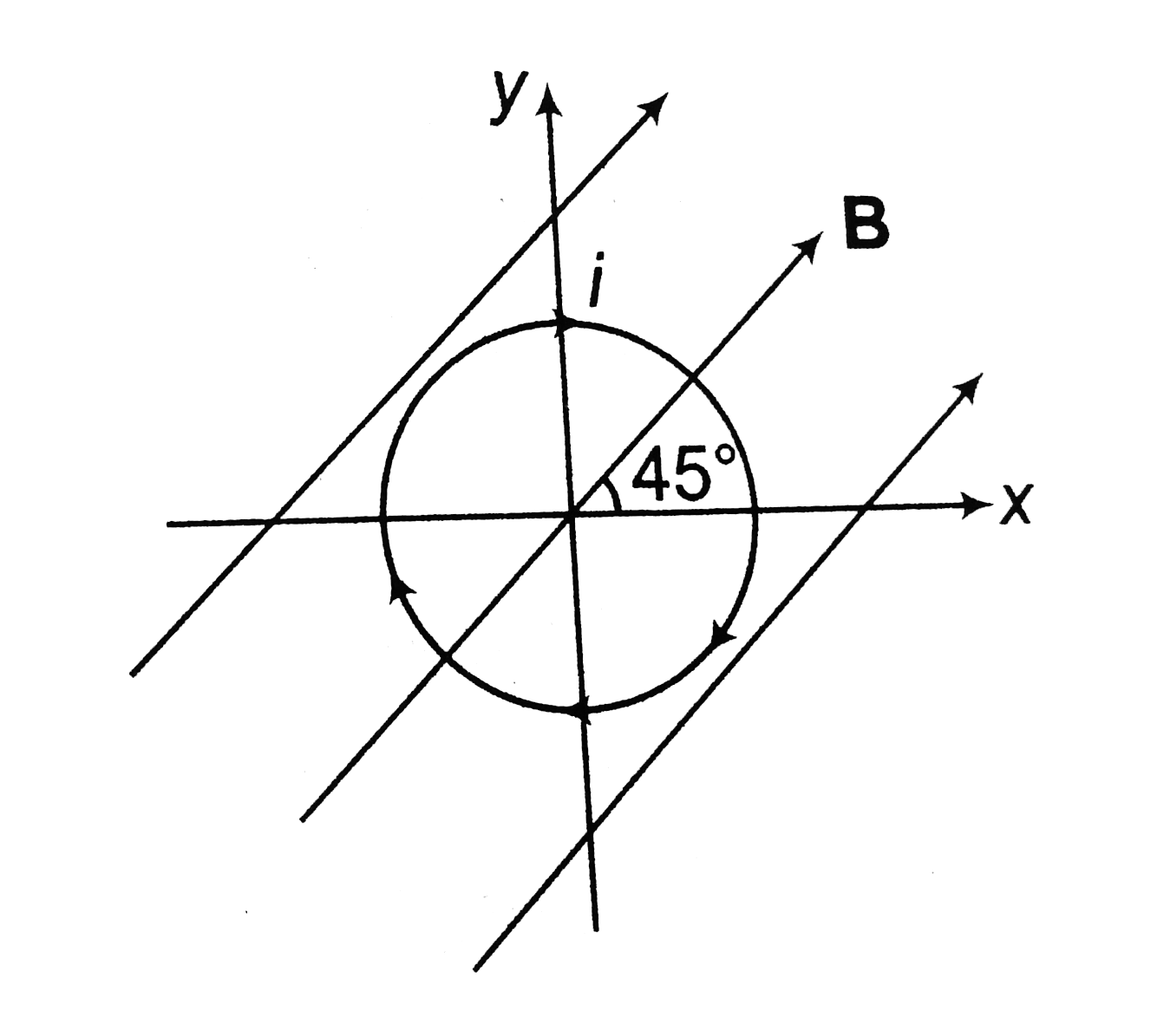
View SolutionA circular loop of radius R=20 cm is placed in a uniform magnetic field B=2T in xy-plane as shown in figure. The loop carries a current i=1.0A in the direction shown in figure. Find the magnitude of torque acting on the loop.

View SolutionA circular loop with N turns has radius r . It lies in the x-y plane carrying current I in the anti-clockwise direction . If the magnetic field in the region is →B=B0ˆi , then find the torque (→r) acting on the loop .
View SolutionA current of2⋅00A exists in a square loop of edge 10⋅0cm. Find the magnetic field B at the centre of the square loop.
View SolutionA square loop of side 6cm carries a current of 30A. Calculate the magnitude of magnetic field B at a point P lying on the axis of the loop and a distance√7 cm from centre of the loop.
View SolutionAn electric current I flows through a circular loop as shown in Figure 2(b) below. Write an expression and direction for the magnetic field at the centre of the loop at point P.

View SolutionA circular loop of radius r carries a current i. where should a long , straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the centre becomes zero?
View SolutionTwo infinitely long straight wires lie in the xy-plane along the lines x=±R. The wire located at x=+R carries a constant current I1 and the wire located at x=−R carries a constant current I2. A circular loop of radius R is suspended with its centre at (0,0,√3R) and in a plane parallel to the xy-plane. This loop carries a constant current ? in the clockwise direction as seen from above the loop. The current in the wire is taken to be positive if it is in the +ˆJ direction. Which of the following statements regarding the magnetic field →B is (are) true?
View SolutionA circular loop of radius a, carrying a current I, is placed in a tow dimensional magnetic field. The centre of the loop coincides with the centre of the filed The strenght of the magnetic field at the pariphery of the loop is B. find the magnetic force on the wire.

View SolutionA circular wire loop of radius R is placed in the X-Y plane with its centre at the origin. The loop carries a current I in the clockwise direction when viewed from a point on the positive Z-axis. A uniform magnetic field →B=B0(ˆi+√3ˆj2) exists in the region x>R√32. The magnitued of the magnetic force on the loop due to the magnetic field is B0IRn. The value of n is______________.
View Solution

