Suppose a nucleus initally at rest undergoes α decay according to equation
.23592X→Y+α
At t=0, the emitted α-partilces enter a region of space where a uniform magnetic field →B=B0ˆj and elcertis field →E=E0ˆi exist. The α-prticles enters in the region with velocity →V=v0ˆj from x=0. At timet=√3×106m0q0E0s, the particle was observed to have speed twice the initial velocity v0. Then, find (a) the velocity v0 of the α-particles,
(b) the initial velocity v0 of the α-particle, (c ) the binding energy per nucleon of the α-particle.
[Given thatm(Y)=221.03u,m(α)=4.003u,m(n)=1.09u,m(P)=1.008u].
The correct Answer is:107ms−1
Charge on α-particle,qα=4×1.6×10−19C and 1u=931MeV/c2. Force acting on α- particle,
→FB=q(→v×→B)+qαE0ˆi
Hence, the particle will move in a circular path in yzPlane . In the same time, it will move x-direction. Hence, resulting path will be a helical spiaral with increasing pitch. Thus,velocity of the circulating α-particles after time t.
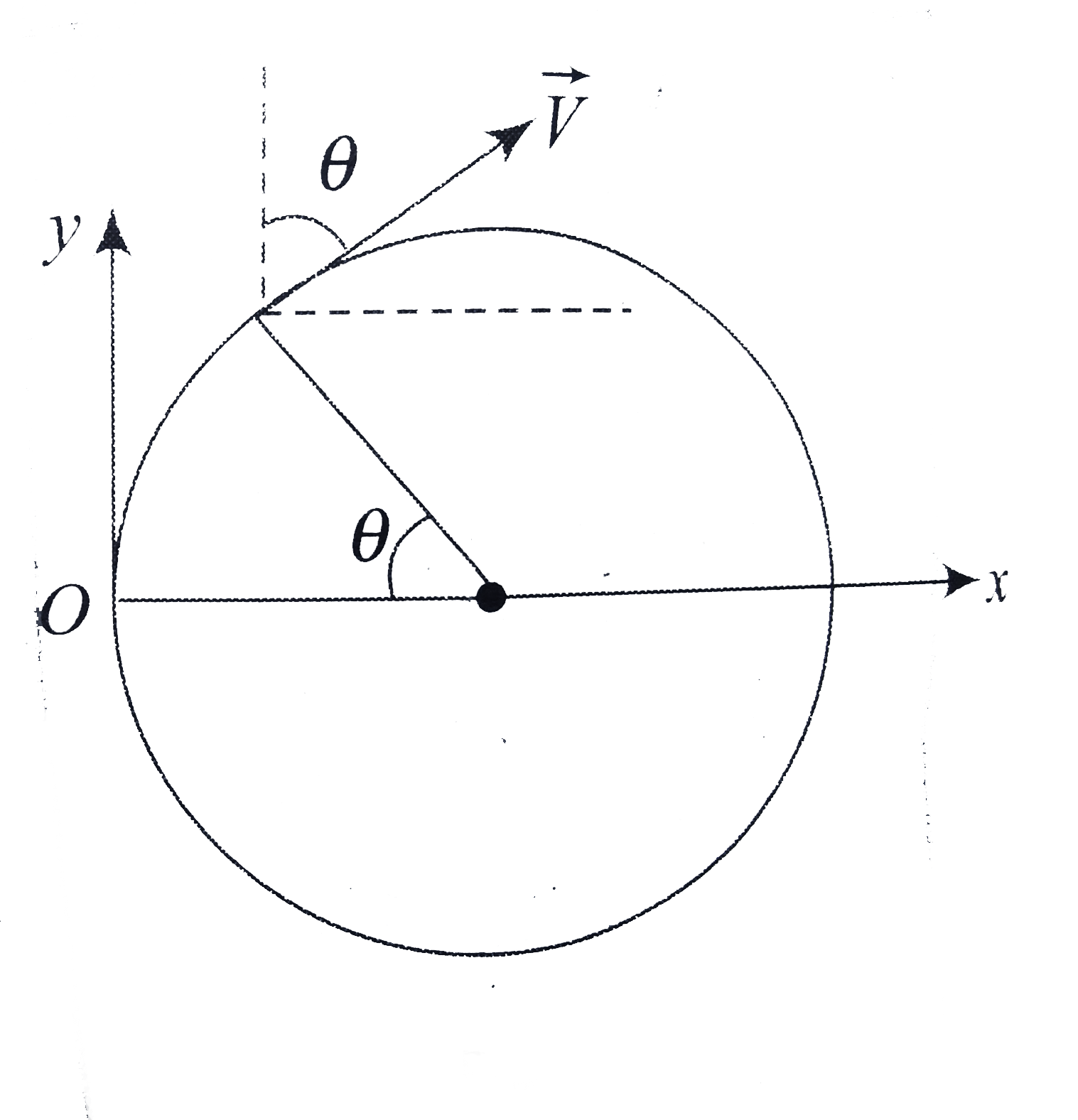
→v0=v0cosθˆj−v0sinθˆk
Due to electric field present, the velocity of the α-particle will incerease along x-axis . Hence, velocity of α particle along x-axis,
→vx=q0E0m0tˆi
Hence,velocity of α-particle,
→v=(q0E0tm0)ˆi+v0cosθˆj−v0sinθˆk (i)
θ=ωt=2πtT
where T=2πmqαB
Hence ,
→v=(q0B0m0)tˆi+v0cos(2πtT)ˆj−v0sin(2πT)ˆk (ii)<br>Give,|vecv|=2v_(0), at t=sqrt3xx10^(7) (m_(0))/(q_(0)E_(0))s<br>4v_(0)^(2)=(sqrt2xx10^(7))^(2)+v_(0)^(2)<br>because v_(0) =10^(7) m s^(-1)<br>Whenanalpha−partic≤isemiedwithvelocityv_(0)omastatio≠ryνc≤us X,decay∏uct(νc≤usY)recoils.Hence,<br>m_(Y)V=m_(alpha)v_(0)<br>rArr V=(m_(alphav))/(m_(Y))=1.811xx10^(5) m s^(-1).
Topper's Solved these Questions
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Single Correct Option
182 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Linked Comprehension
29 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Exercise 5.2
27 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Integer Type
4 Videos
Similar Questions
Suppose a nucleus initally at rest undergoes α decay according to equation
.22592X→Y+α
At t=0, the emitted α-particles enter a region of space where a uniform magnetic field →B=B0ˆi and elecrtic field →E=E0ˆi exist. The α-particles enters in the region with velocity →V=v0ˆj from x=0. At timet=√3×106m0q0E0s, the particle was observed to have speed twice the initial velocity v0. Then, find (a) the velocity v0 of the α-particles,
(b) the initial velocity v0 of the α-particle, (c ) the binding energy per nucleon of the α-particle.
[Given thatm(Y)=221.03u,m(α)=4.003u,m(n)=1.09u,m(P)=1.008u].
View SolutionA rectangular loop of dimensions (a×b) carries a current i. A uniform magnetic field →B=B0ˆi exists in space. Then :
View SolutionAn alpha particle moving with the velocity →v=uˆi+ˆj ,in a uniform magnetic field →B=Bˆk . Magnetic force on alpha particle is
View SolutionElectric field and magnetic field in a region of space are given by(Ē= E_0 hat j). and (¯¯¯B=B0ˆj). A charge particle is released at origin with velocity (¯v=v0ˆk) then path of particle is
View SolutionA particle of spectfic charge α enters a uniform magnetic field B=−B0ˆk with velocity V=v0ˆi from the origin Find the time dependence of velocity and position of the particle
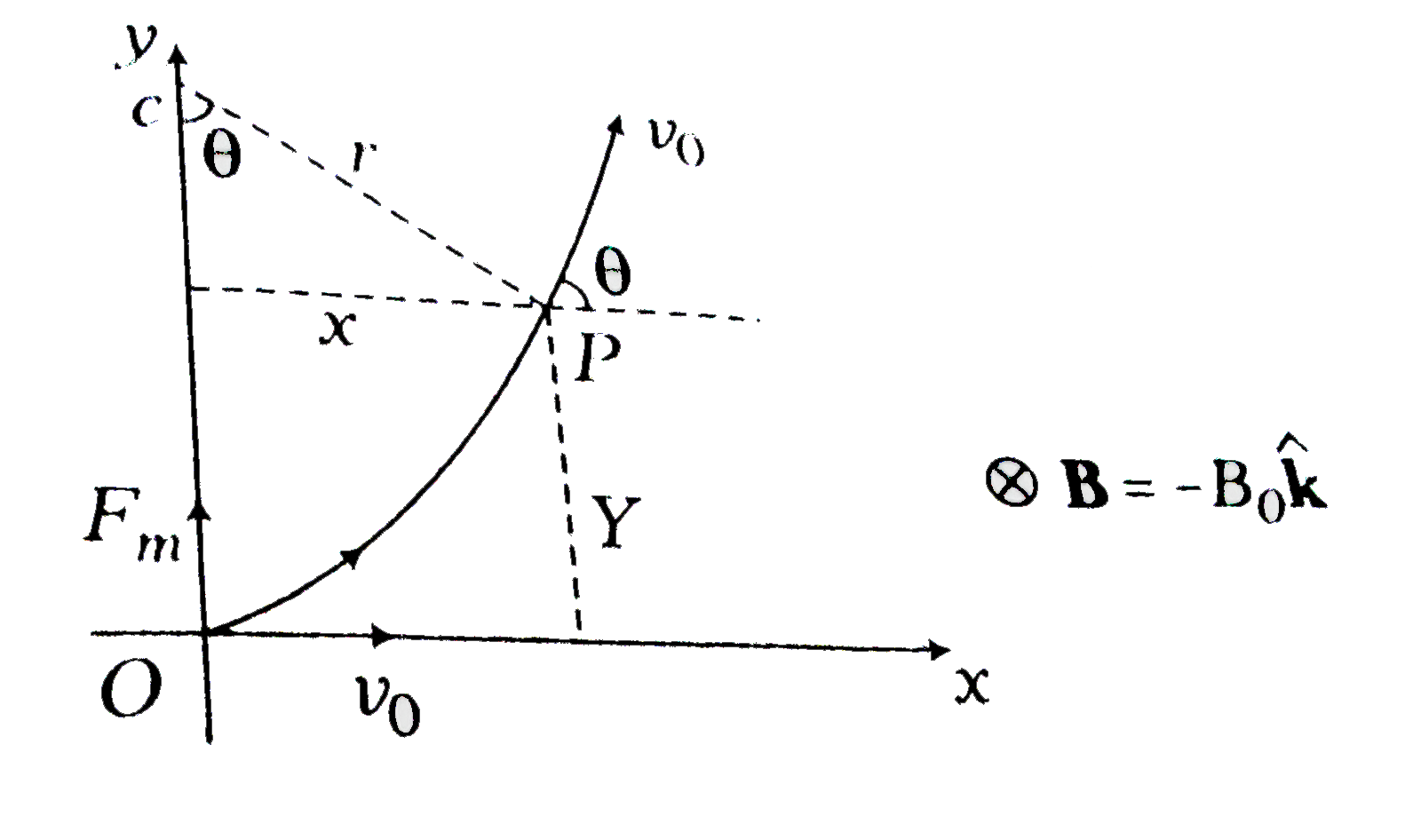
View SolutionA positively charged particle is moving along the positive x-axis in a unifom electric field→E=E0ˆj and magnetic field →B=B0ˆk (where E0 and B0 are positive constants), then
View SolutionA conductor AB of length l moves in xy plane with velocity →v=v0(ˆi−ˆj). A magnetic field →B=B0(ˆi+ˆj) exists in the region. The induced emf is
View SolutionIn a region of space , suppose there exists a uniform electric field →E=10ˆi(Vm) . If a positive charge moves with a velocity →v=−2ˆj, its potential energy
View SolutionA particle of specific charge alpha enters a uniform magnetic field B=−B0ˆk with velocity v=v0ˆi from the origin. Find the time dependence of velocity and position of the particle.

View SolutionA portion is fired from origin with velocity →v=v0ˆj+v0ˆk in a uniform magnetic field →B=B0ˆj. In the subsequent motion of the proton
View Solution
