A sample of .18F is used internally as a medical diagnostic tool to look for the effects of the positron decay (T1/2=110min) . How long does it take for 99% of the .18F to decay?
The correct Answer is:12.2h
Radioactive deacy equation is
N=N0e−λt=N0e−1n(2)t/T (∵λ=In2T)
After decay of 99% of the initial sample, only 1% will be left, i.e., N/N0=1%
∴NN0=1100=e−1n(2)t/T
If we take the natural logarithm, we have
−1n100=−1n2×tT
Which on solving for t yields
t=1n1001n2×T=log100log2×T
=20.3010×10=731min=12.2h.
Topper's Solved these Questions
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Single Correct Option
182 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Linked Comprehension
29 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Exercise 5.2
27 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Integer Type
4 Videos
Similar Questions
One end of a cylindrical glass rod (mu = 1.5) of radius 1.0 cm is rounded in the shape of a hemisphere. The rod is immersed in water (mu= 4/3) and an object is placed in the water along the axis of the rod at a distance of 8.0 cm from the rounded edge. Locate the image of the object.
View SolutionHydrogen peroxide H2O2 (aq) decomposes to H2O(l) and O2(g) in a reaction that is first order in H2O2 and has a rate constant k=1.06×103−1min
(i) How long will it takes for 15% of a sample of H2O2 to decompose?
(ii) How long will it take for 87.5% of the sample to decompose?
View Solution
Knowledge Check
A nucleus of Ux1 has a half life of 24.1 days. How long a sample of Ux1 will take to change to 90% of Ux2.
A80 daysB40 daysC20 daysD10 days
Strontium 90 is one of the harmful nuclides resulting from nuclear fission explosions.
Strontium 90 decays by beta particle emission with a half life of 28 years. How long (in years) would it take for 99.0% of a sample of strontium-90 released in an atmospheric test of an atomic bomb to decay? (log 2 = 0.30)
View SolutionA girl is standing on the top edge of an 18 m high building. She tosses a coin upwards with a speed of 7.0ms−1.How long does it take for the Coin to hit the ground ?How fast is the coin going just before it strikes the ground? (g=10ms−2)
View SolutionA cell of e.m.f. 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and a resistor of 4.5 Ω as shown in Fig.
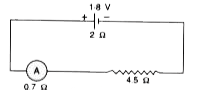
What would be the reading of the ammeter ?
View Solution(a). It is known that density ρ of air decreases with height y as
ρ=ρ0e−y/y(_o) ltb rgt where po=1.25kgm−3 is the density at sea level, and yo is a constant. This density variation is called the law of atmospheres. Obtain this law assuming that the temperature of atmosphere remains a constant (isothermal conditions). Also assume that the value of g remains constant
(b). A large He balloon of volume 1425m3 is used to lift a payload of 400 kg. Assume that the balloon maintains constant radius as it rises. How high does it rise?
[take yo=8000mandρHe=0.18kgm−3]
View Solution36% amount of a radioactive sample disintegrates in t time. Calculate how much percentage fraction will decay in t/2 time.
View SolutionRadioactive decay follows first-order kinetic. The mean life and half-life of nuclear decay process are τ=1/λ and t1/2=0.693/λ. Therefore are a number of radioactive elements in nature, their abundance is directly proportional to half life. The amount remaining after n half lives of radioactive elements can be calculated using the relation:
N=N0(12)n
Half life of .60Co is 5.3 years, the time taken for 99.9% decay will be
View SolutionA hollow sphere of radius 2 cm is attached to an 18 cm long thread to make a pendulum. Find the time period of oscillation of this pendulum . How does it differ from the time period calculated using the formula for a simple pendulum?
View Solution
