In Young's experiment, find the distance between two slits that results in the third minimum for $420 n m$ violet light at an angle $30^{\circ}$
.

Video Solution

Text Solution

Verified by Experts

$S_{2} L = d \sin θ$
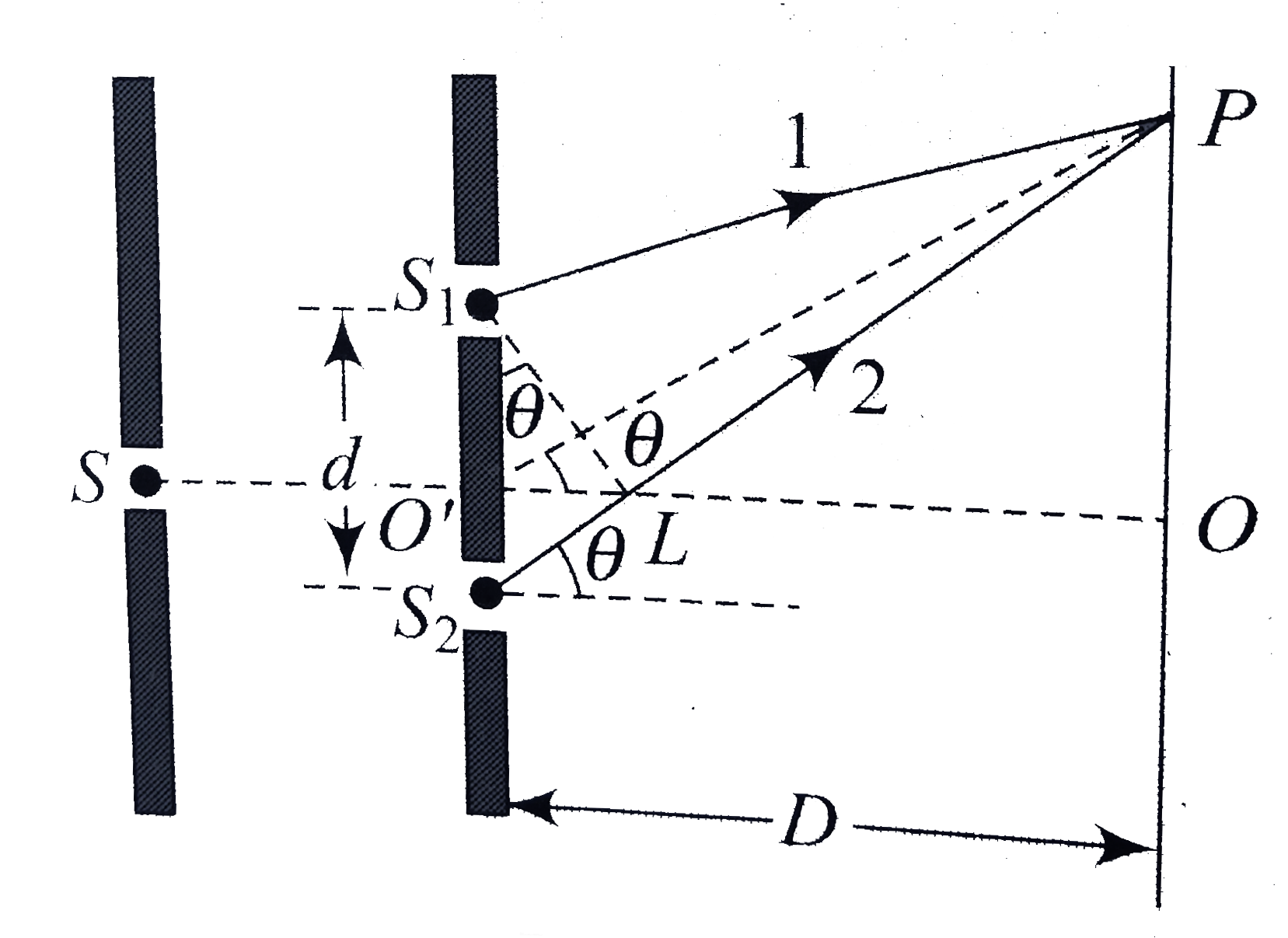or $Δ x = d \sin θ$
For intensity to be minimum,
$Δ x = \sin θ$
$Δ x = (2 n - 1) λ / 2$
$n = 1, 2, 3, \dots$
For third minimum, $n = 3$
$d \sin θ = \frac{5 λ}{2}$
Given: $λ = 420 n m = 420 \times 10^{- 9} m$
$θ = 30^{\circ}$
$∴ d {\sin 30}^{\circ} = \frac{5}{2} \times 420 \times 10^{- 9} \Rightarrow d = 2.1 \times 10^{- 6} m$ .

Updated on:21/07/2023

In Young's double slit experiment, the distance between two sources is $0.1 m m$ . The distance of screen from the sources is $20 c m$ . Wavelength of light used is $5460 Å$ . Then angular position of the first dark fringe is
A ${0.08}^{\circ}$
B ${0.16}^{\circ}$
C ${0.20}^{\circ}$
D ${0.31}^{\circ}$