A real point source is 5cm away from a plane mirror whose reflectinig ability is 50% , while the eye of an observer (pupil diameter 5mm) is 10cm away form the mirror. Asuume that both source and eye are on the same line perpendicular to the surface and refracted rays have no effect on intensity. Then,
the area of the mirro used in observing the image of source is (25π/36)mm2
the area of the mirror used in observing the image of source is 25πmm2
the ratio of the intensities of light as received by the observer in the presence to that in the absence of mirror is (10/9)
the ratio of the intensities of light as received in the presence to that in the absence of mirror is 19/18
The correct Answer is:a.,d.
To solve the problem step by step, we need to analyze the situation involving a point source, a plane mirror, and an observer's eye. Let's break it down:
Step 1: Understand the Setup
- A real point source (S) is located 5 cm away from a plane mirror (M).
- The observer's eye (O) is 10 cm away from the mirror.
- The mirror has a reflecting ability of 50%.
Step 2: Determine the Image Location
- The image (I) of the point source formed by the plane mirror will be located 5 cm behind the mirror. Thus, the distance from the mirror to the image is also 5 cm.
Step 3: Calculate the Total Distance from Source to Observer
- The total distance from the source to the observer can be calculated as follows:
- Distance from source to mirror = 5 cm
- Distance from mirror to observer = 10 cm
- Total distance (S to O) = 5 cm + 10 cm = 15 cm
Step 4: Determine the Pupil Diameter
- The diameter of the observer's pupil is given as 5 mm, which is equivalent to 0.5 cm.
Step 5: Set Up Similar Triangles
- We can use similar triangles to relate the distances and the diameters involved:
- Let A be the point where the light rays from the source reach the mirror.
- Let B be the point where the reflected rays reach the observer's eye.
- The triangles formed by the image and the observer's eye can be used to find the effective area of the mirror that contributes to the observer's view.
Step 6: Calculate the Effective Area of the Mirror
- The area of the mirror that contributes to the observer's view can be calculated using the ratio of the pupil diameter to the distance from the observer to the image.
- Using the similarity of triangles:
IPPC=IAAB
where:
- IP = distance from image to observer
- PC = distance from the pupil to the mirror
- IA = distance from source to image
- AB = distance from source to observer
Step 7: Calculate the Intensity of Light
- The intensity of light received by the observer can be calculated for both cases (with and without the mirror):
- Without the mirror:
I1=P4π(52)
- With the mirror:
- The intensity is halved due to the 50% reflection ability of the mirror:
I2=P/24π(152)
Step 8: Calculate the Ratio of Intensities
- The ratio of the intensity with the mirror to the intensity without the mirror can be expressed as:
I2I1=P/24π(152)P4π(52)
- Simplifying this gives:
I2I1=1/2⋅(52)(152)=25/2225=25450=118
Final Answer
The ratio of the intensity of light received by the observer in the presence of the mirror to that in the absence of the mirror is 1918.
- A real point source (S) is located 5 cm away from a plane mirror (M).
- The observer's eye (O) is 10 cm away from the mirror.
- The mirror has a reflecting ability of 50%.
- The image (I) of the point source formed by the plane mirror will be located 5 cm behind the mirror. Thus, the distance from the mirror to the image is also 5 cm.
- The total distance from the source to the observer can be calculated as follows:
- Distance from source to mirror = 5 cm
- Distance from mirror to observer = 10 cm
- Total distance (S to O) = 5 cm + 10 cm = 15 cm
- The diameter of the observer's pupil is given as 5 mm, which is equivalent to 0.5 cm.
- We can use similar triangles to relate the distances and the diameters involved:
- Let A be the point where the light rays from the source reach the mirror.
- Let B be the point where the reflected rays reach the observer's eye.
- The triangles formed by the image and the observer's eye can be used to find the effective area of the mirror that contributes to the observer's view.
- The area of the mirror that contributes to the observer's view can be calculated using the ratio of the pupil diameter to the distance from the observer to the image.
- Using the similarity of triangles:
IPPC=IAAB
where:
- IP = distance from image to observer
- PC = distance from the pupil to the mirror
- IA = distance from source to image
- AB = distance from source to observer
- The intensity of light received by the observer can be calculated for both cases (with and without the mirror):
- Without the mirror:
I1=P4π(52)
- With the mirror:
- The intensity is halved due to the 50% reflection ability of the mirror:
I2=P/24π(152)
- The ratio of the intensity with the mirror to the intensity without the mirror can be expressed as:
I2I1=P/24π(152)P4π(52)
- Simplifying this gives:
I2I1=1/2⋅(52)(152)=25/2225=25450=118
The ratio of the intensity of light received by the observer in the presence of the mirror to that in the absence of the mirror is 1918.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
A concave mirror forms an image of 20 cm high object on a screen placed 5.0 m away from the mirror. The height of the image is 50 cm. Find the focal length of the mirror and the distance between the mirror and the object.
View Solutiona sound source emits frequency of 180hZ when moving towards a rigid wall with speed 5m/s and an observer is moving away from with speed 5m/s. Both source and observer moves on a straight line which is perpendicular to the wall. The number of beatd per second heard by the observer will be [speed of sound = 335m/s]
View SolutionA point source is at a distance 35cm on the optical axos from a spherical mirror having a focal length 25cm. At what distance measured along the optical axis form the concave mirror should a plane mirror (perpendicualr to principle axis) be placed for the image it forms (due to rays falling on it after reflection from the concave mirror) to coincide with the point source?
View SolutionConcave mirror forms the real image of a point source lying on the optical axis at a distance of 50 cm from the mirror. The focal length of the mirror is 25 cm. The mirror is cut into and its halves are drawn a distance of 1 cm apart in a direction perpendicular to the optical axis. How will the image formed by the halves of the mirror be arranged?
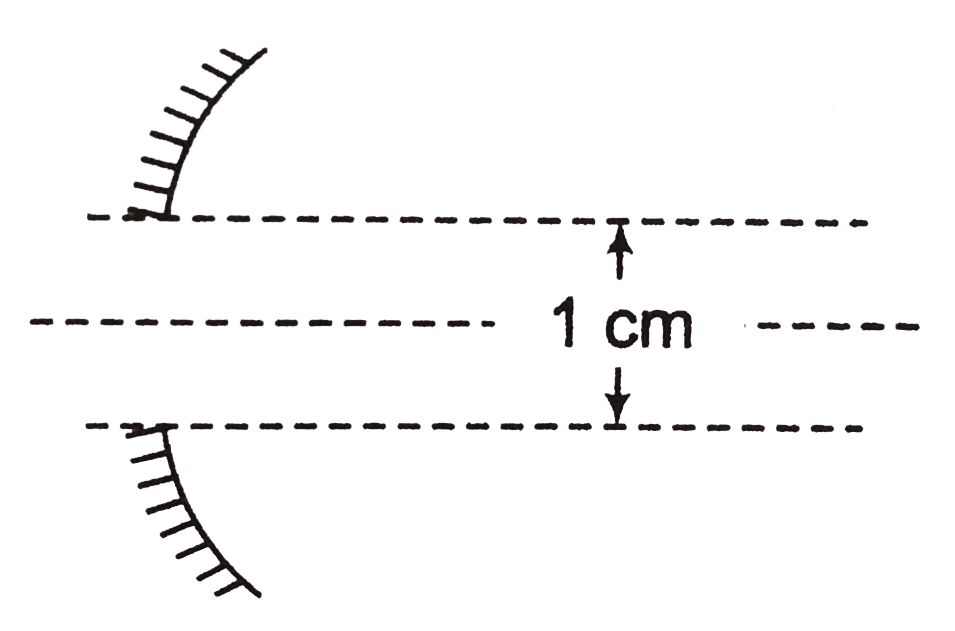
View SolutionA concave mirror forms real image of a point source lying on the optical axis at a distance of 50cm from the mirror. The focal length of the mirror is 25cm. The mirror is cut in two, and its halves are drawn at a distance of 1 cm apart in a direction perpendicular to the optical axis.

Q. The distance between the two images formed by the two halves of the mirror is
View SolutionA concave mirror forms real image of a point source lying on the optical axis at a distance of 50cm from the mirror. The focal length of the mirror is 25cm. The mirror is cut in two, and its halves are drawn at a distance of 1 cm apart in a direction perpendicular to the optical axis.

Q. In the given situation, if the two halves are each rotated (before being separated) about S by 90∘, with reference to original position, then the distance between the two images will be

View SolutionAn object is placed 21 cm in front of a concave mirror of radius of curvature 10cm. A glass slabe of thickness 3cm and refractive index 1.5 is then placed close to the irror in the space between the object and the mirror. The distance of the near surface of the slabe from the mirror is 1cm. The final image from the mirror will be formed at
View SolutionA plane mirror 50cm long, is hung on a vetical wall of a room, with its lower edge 50cm above the ground. A man stands of the mirror at a distance 2m away from the mirror. If his eyes are at a height 1.8m above the ground, then the length (distance between the extreme points of the visible region perpendicular to the mirror ) of the floor visible to him due to refliection from the mirror is x26m . Find the value of x
View SolutionBehind a thin converging lens having both the surfaces of the same radius 10cm, a plane mirror has been placed. The image of an object at a distance of 40 cm from the lens is formed at the same position. What is the refractive index of the lens?

View SolutionA concave mirror forms real image of a point source lying on the optical axis at a distance of 50cm from the mirror. The focal length of the mirror is 25cm. The mirror is cut in two, and its halves are drawn at a distance of 1 cm apart in a direction perpendicular to the optical axis.

Q. Two statements are provided. Choose which is true and which is false.
Statement I: Image formed by half cut mirror has just half the intensity as that of the intensity of image formed by complete mirror.
Statement II: More the lateral separation between the two halves of the mirror, less will be the separation between the two images, as show in the given situation.
View Solution
