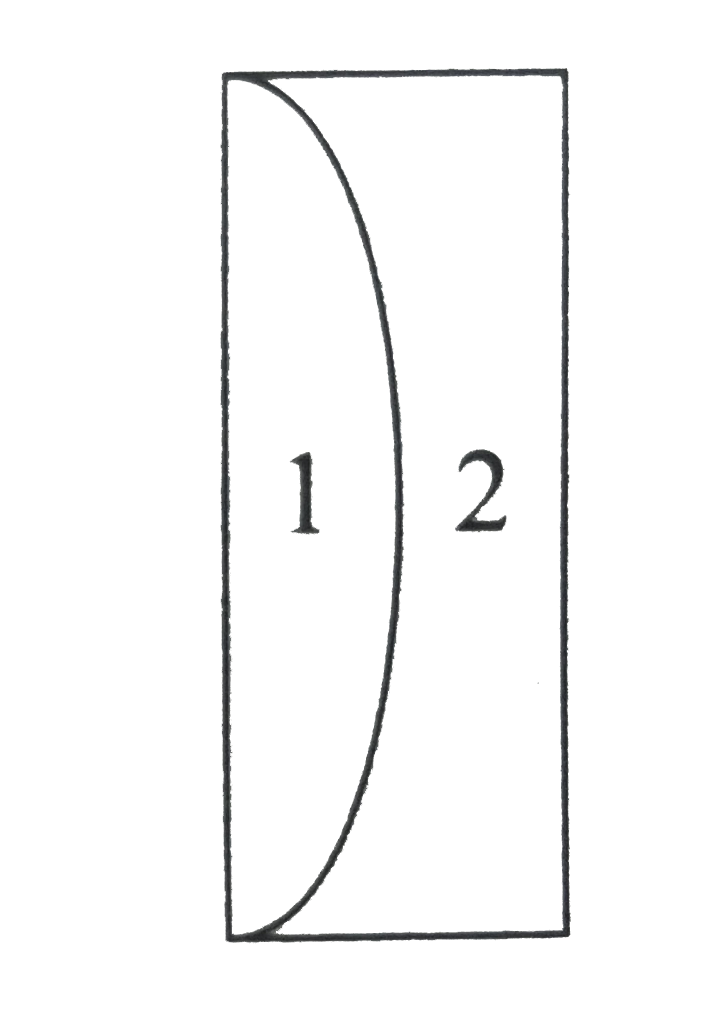
A plano- convex lens fits exactly into a plano- concave lens. Their plane surfaces are parallel to each other. If lenses are made of different materials of refractive indices μ1 and μ2 and R is the radius of curvature of the curved curface of the lenses, then the focal length of the combination is
Rμ1−μ2
2Rμ2−μ1
R2(μ1−μ2)
R2−(μ1−μ2)
The correct Answer is:a.
1F=(μ−1)(1∞+1R)+(μ2−1)(1−R−1∞)
=μ1−μ2R or F=Rμ1−μ2
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
A plano-convex lens fits exactly into a plano-concave lens. Their plane surfaces are parallel to each other. If the lenses are made of different material of refractive indices μ1 and μ2 and R is the radius of curvature of the curved surface of the lenses, then focal length of the combination is
View SolutionA plano convex lens fits exactly into a plano concave lens. Their plane surfaces are parallel to each other. If the lenses are made of different materials refractive indices μ1 and μ2 and R is the radius curvature of the curved surface of the lenses, the focal length of the combination is
View Solution
Knowledge Check
What is the refractive index of material of a plano-convex lens , if the radius of curvature of the convex surface is 10 cm and focal length of the lens is 30 cm ?
A65B74C23D43
A plano convex lens fits exactly into a plano concave lens. Their plane surfaces are parallel to each other. If the lenses are made of different materials refractive indices μ1 and μ2 and R is the radius curvature of the curved surface of the lenses, the focal length of the combination is
View SolutionA plano convex lens fits exactly into a plano concave lens. Their plane surfaces are parallel to each other. If lenses are made of different materials of refractive index μ1=4/3 and μ2=6/5 and R = 40 cm is the radius of curvature of the curved surface of the lenses, then the focal length of combination (in meters) is.
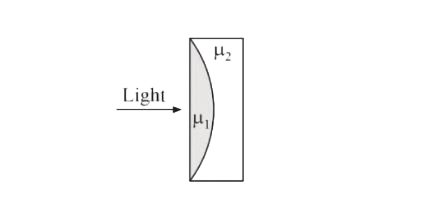
View SolutionA plano convex lens fits exactly into a plano concave lens. Their plane surfaces are parallel to each other. If lenses are made of different materials of refractive index μ1=4/3 and μ2=6/5 and R = 40 cm is the radius of curvature of the curved surface of the lenses, then the focal length of combination (in meters) is.
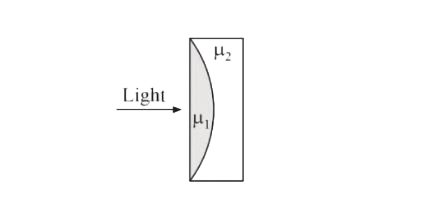
View SolutionA thin plano-convex lens fits exactly into a thin plano-concave lens. Their plane surfaces are parallel to each other. The lenses are made of different material of refractive indices μ1 and μ2 and R is the radius of curvature of the curved surfaces of the lenses, if rays are incident parallel to principal axis on lens of refractive index.
View SolutionA planocovex lens is made of a material of refractive in μ=1.5 The radius of curvature of curved surface of the lens is 20.cm. If its plane surface3 is silvered, the focal length of the silvered lens will be
View SolutionFind the refractive index of the material of a plano-convex lens, if the radius of curvature of the convex surface is 20 cm and focal length of the lens is 60 cm?
View SolutionA thin plano-convax lens fits exactly into a plano concave lens with their plane surface parallel to each other as shown in the figure.the radius of the curvature of the curved surface R=30cm The lens are made of different material having refractive indexμ1=32and μ2=54as shown in the figure
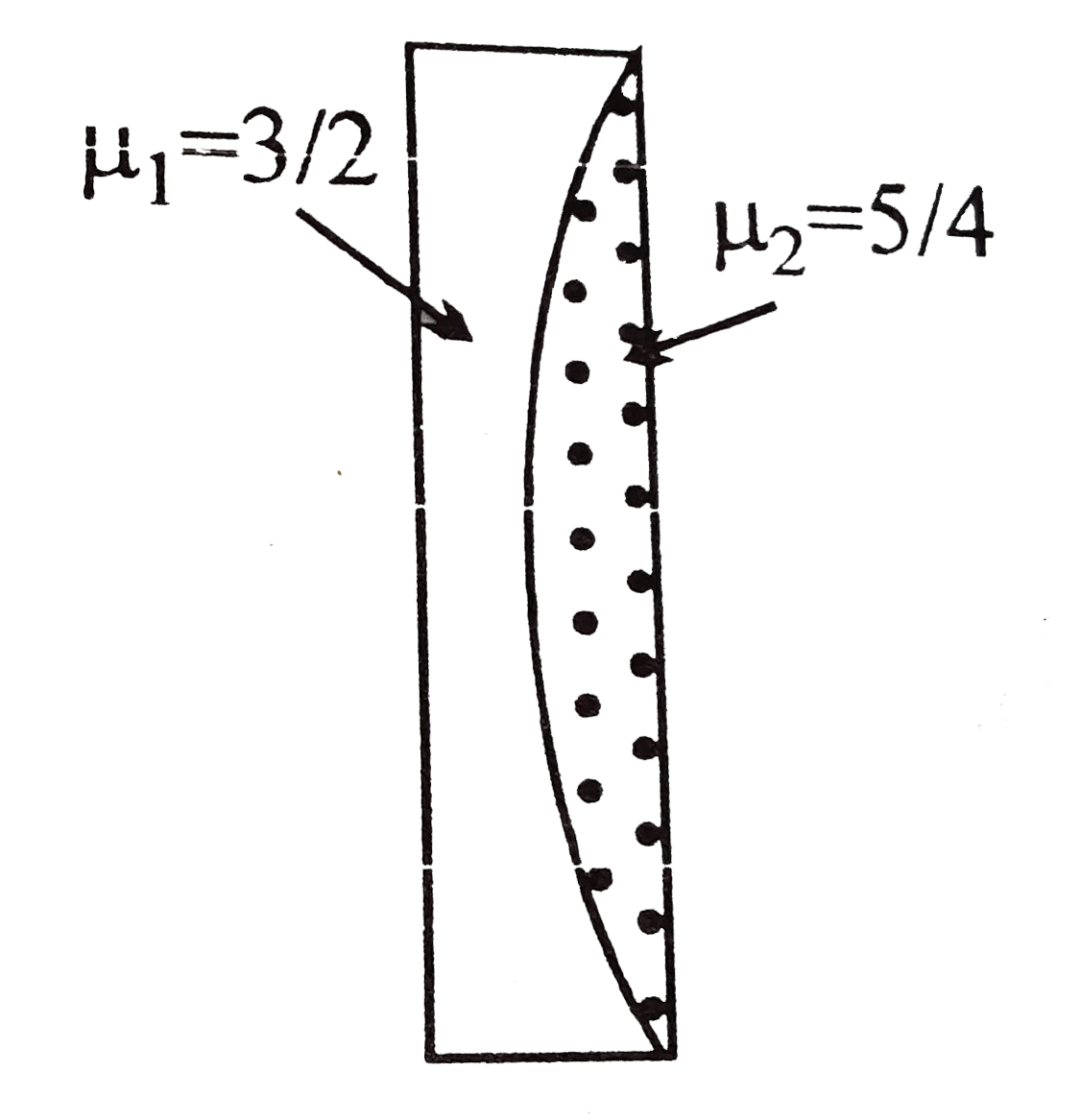
(i) if plane surface of the plano -convex lens is silvered,then calculate the equivalent focal length of this system and also calculate the nature of this equivalent mirror .
(ii) An object having transverse length 5cmis placed on the axis of equivalent mirror(in part1)atadistance15cm from the equivalent mirror along principal axis.Find the transverse magnification produced by equivalents mirror.
View Solution
