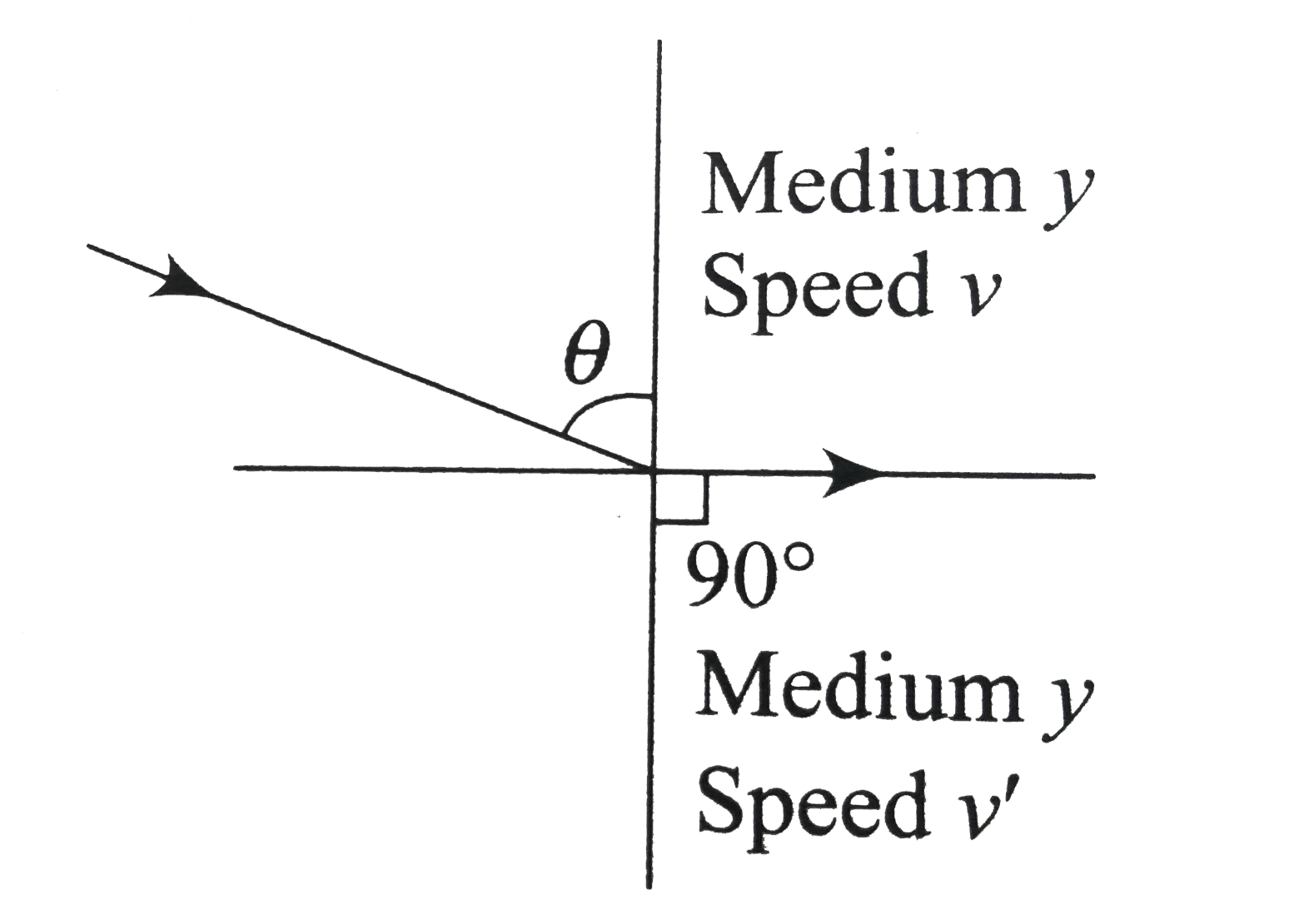
The critical angle of light from medium A to medium B is θ. The speed of light in medium A is v. the speed of light in medium B is
v cosθ
v/cosθ
vsinθ
v/sinθ
The correct Answer is:d.
Clearly, x is denser medium.
Now, sinθsin90∘=1YμX
XμY=vv′
or v′=vsinθ
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
Knowledge Check
Critical angle for light going from medium (i) to (ii) is θ . The speed of light in medium (i) is v then speed in medium (ii) is
Av(1−cosθ)BvsinθCvcosθDv(1−sinθ)Consider two adjacent transparent media. The speed of light in medium 1 is v1, and the speed of light in medium 2 is v2. If v1<v2, then total internal reflection will occur at the interface between these media if a beam of light is
Aincident in medium 1 and strikes the interface at an angle of incidence greater than sin−1(v1/v2).Bincident in medium 1 and strikes the interface at an angle of incidence greater than sin−1(v2/v1).Cincident in medium 2 and strikes the interface at an angle of incidence greater than sin−1(v1/v2).Dincident in medium 2 and strikes the interface at an angle of incidence greater than sin−1(v2/v1).
If critical angle for TIR from medium to vacuum is 45 deg then velocity of light in medium
View SolutionThe speed of light in an isotropic medium depends on
View SolutionThe dispersion of light in a medium implies that :
View SolutionFind the speed of light in medium 'a' if speed of light in medium 'b' is c/3, where c =speed of light in vacuum and light refracts from medium 'a' to medium 'b' making 45∘ and 60∘, respectively, with the normal.
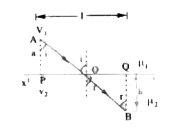
View SolutionThe time required for the light to go from A to B, when a ray of lilght goes from point A in a medium where the speed of light is v1 to a point B in a medium where the speed of light is v2 as shown in figure is
View SolutionThe refractive index of a medium 'x' with respect to a medium 'y' is 23 and the refractive index of medium 'y' with respect to medium 'z' is 43. Find the refractive index of medium 'z' with respect to medium 'x' . If the speed of light in medium 'x' is 3×108ms−1, Calculate the speed of light in medium 'y'.
View Solution
